变换,指将数据通过一定的规则进行转换,通常可以用矩阵来进行表示。
简介
- 在计算机图形学中,变换的使用非常常见,如:平移、缩放、旋转等。变换主要分为
- 线性变换
- 可以保留矢量加和标量乘的变换,即
f(x) + f(y) = f(x + y)kf(x) = f(kx)
- 缩放(scale)、旋转(rotation)、错切(shear)、镜像(mirroring)、正交投影(orthography projection)等
- 可以保留矢量加和标量乘的变换,即
- 仿射变换
- 线性变换和平移变换的合并
- 线性变换
- 对于常见的变换,其变换矩阵分别为
- 平移
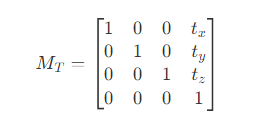
- 缩放
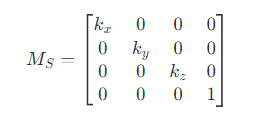
- 旋转(绕x、y、z轴)
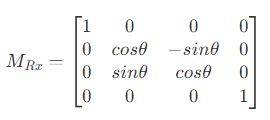
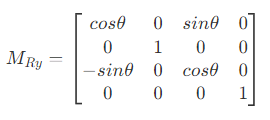
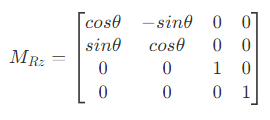
- 平移
- 对于复合变换,需要按照先缩放,再旋转,最后平移的顺序,才能保证最后得到正确的效果。
- 在 Unity 中,坐标系是按照
y-x-z的逐级组合的,如果绕世界坐标系下的固定坐标轴旋转,需要按照 zxy 的顺序。如果绕自身坐标系旋转,由于旋转时自身坐标系也会发生改变,根据坐标系的次序,需要按照 yxz 的顺序进行旋转,即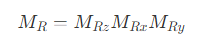
- 在图形学计算中,从CPU传入的顶点坐标,需要从模型空间,变换到世界空间,再变换到观察空间,再变换到裁剪空间,最后变换到屏幕空间。从模型空间变换到裁剪空间,就是常说的 MVP 变换。
模型变换
- 模型变换,即将坐标从模型空间变换到世界空间。在 Unity 中,如果一个 GameObject 没有父节点,那么其坐标即为世界空间下的坐标。如果存在父节点,则其自身坐标即为模型空间下的坐标,需要进行变换。变换为复合变换,将所有父节点的信息累计起来,进行平移、缩放和旋转。假设父节点的坐标为
(x,y,z),角度为(θ,0, 0),则最终模型变换的变换矩阵即为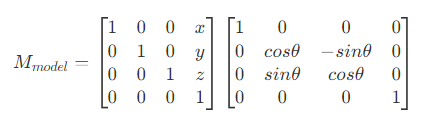
观察变换
- 相机决定了渲染使用的视角,在观察空间下,相机的坐标为原点坐标,x轴正向为右方,y轴正向为上方,
z轴正向为相机后方。尽管 Unity 在模型空间和世界空间下使用的都是左手坐标系,但在观察空间下, Unity 和 OpenGL 一样,使用右手坐标系,因此,相机的正前方为-z。 - 为了将物体变换到观察空间下,需要对应的变换矩阵。若将相机变换到世界坐标下的原点,并旋转到与坐标轴重合,再将相机的 z 方向取反,此时对应物体经过同样的变换后,在世界空间下的信息即为在观察空间下的信息。假设相机在世界空间下的坐标为
(x,y,z),角度为(θ,0, 0),则观察变换矩阵为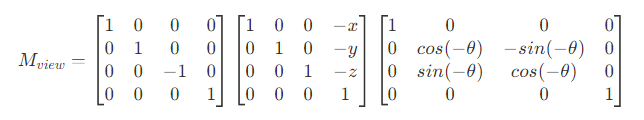
投影变换
- 相机最终渲染的范围为其视锥体范围,在视锥体内的正常渲染,视锥体外的则剔除,与视锥体相交的则会被裁剪,只保留视锥体内的部分。对于正交投影,视锥体是一个长方体,计算对象是否在其范围相对比较简单,而透视投影是一个锥体,计算难度则相对较大。另外,由于每个相机都有各自的参数,所以各自的视锥体都不一样,因此计算起来也更加复杂。为了能统一到一个通用、简单的结构下进行计算,则需要进行投影变换。
- 视锥体的一些表示
l:近裁剪平面的左边r:近裁剪平面的右边t:近裁剪平面的上边b:近裁剪平面的下边n:近裁剪平面的距离(正)f:远裁剪平面的距离(正)
正交投影
- 正交模式下,视锥体是一个长方体,要将长方体视锥体变换到以
(0, 0)为中心,[-1, 1]范围的正方体内,因此需要执行两个步骤- 将视锥体中心移动到坐标原点
- 将视锥体进行缩放,形成
[-1, 1]的正方体
- 所以正交投影矩阵为
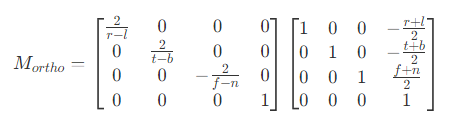
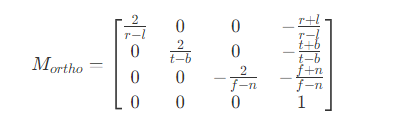
透视投影
- 透视模式下,视锥体是一个截掉顶部的锥体,和正交模式不一样,所以需要进行的操作为
- 将视锥体变换为长方体
- 按照正交投影进行投影变换
- 为了将视锥体变换为长方体,首先需要将视锥体的
x、y坐标投影到近裁剪平面对应的坐标值。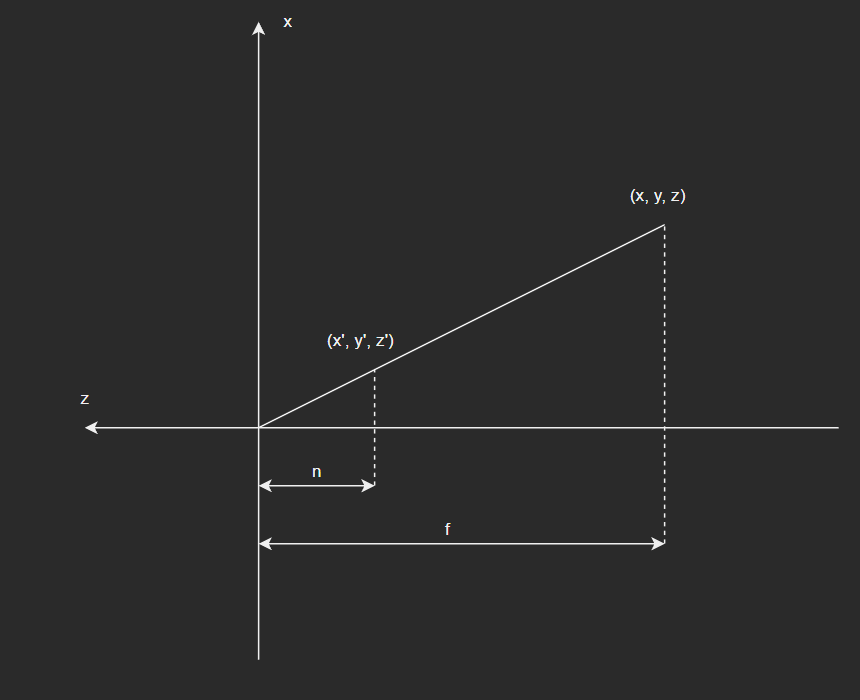
- 可以看到,视锥体上的点的关系为
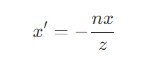
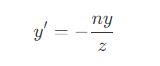
- 因此,变换过程为
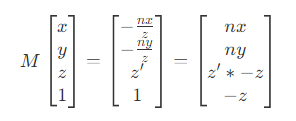
- 可以推出变换矩阵
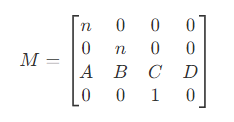
- 由于远近裁剪平面经过变换后,还是保持不变,对于近裁剪平面上的点,
z = z' = -n,则有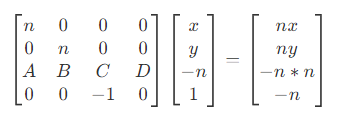
- 因此可以得到,变换矩阵为
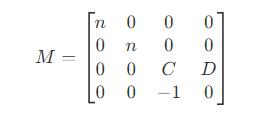
- 同样,对于远裁剪平面上的点,
z = z' = -f,则有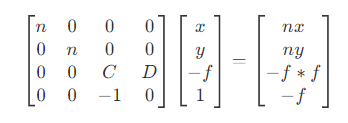
- 可以得到
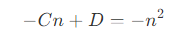
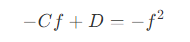
- 因此变换矩阵为
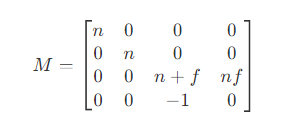
- 则最终透视投影的变换矩阵为
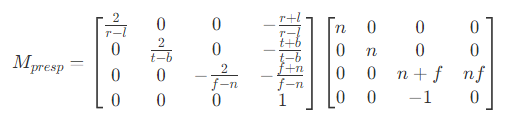
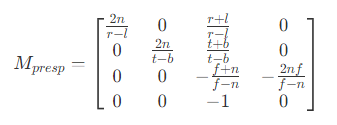
齐次除法(透视除法)
- 经过投影变换后,得到的视锥体,需要投影到屏幕空间中。然而可以发现,正交投影和透视投影得到的视锥体并不是统一的,所以需要统一转换到 NDC(Normalized Device Coordinates)中,即将
x、y、z、w都除以w分量。 - 正交投影变换为
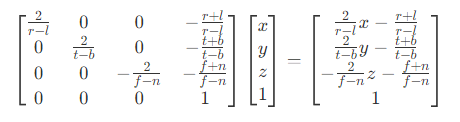 由于
由于 w分量为1,因此齐次除法后保持不变。 - 透视投影变换为
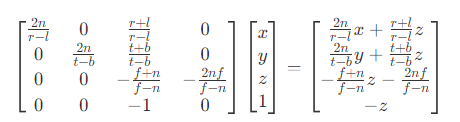 由于
由于 w分量为-z,所以x、y、z都要除以-z,从而将视锥体转换到[-1, 1]范围里,即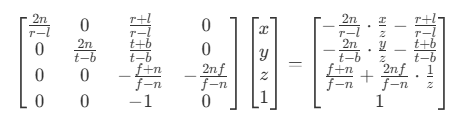
深度值
- 透视投影经过齐次除法后,
z_NDC的值为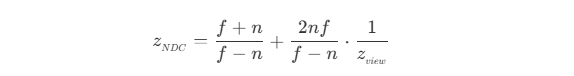
- 在像素着色器中,每一个像素的坐标都需要通过插值计算得到,在透视投影下,需要使用透视校正插值。此时,如果深度图使用观察空间下的
z_view,则在插值过程需要对属性I除以z_view计算,因此深度图使用z_NDC可以减少计算复杂度。 - 由于深度图的范围为
[0, 1],因此深度图中的z_depth值为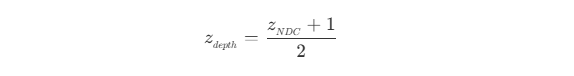
- 可以看到,齐次除法后的
z_NDC值已经不为观察空间下z_view值的线性变换,因此使用深度图的深度信息时,需要变换观察空间下才能进行其他计算,即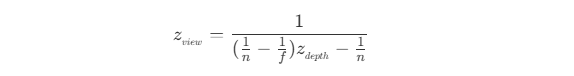
- 由于 OpenGL 中观察空间为右手坐标系,而裁剪空间下是左手坐标系,所以观察空间下的
z_view值需要取反,才为左手坐标系下的线性z_eye值,即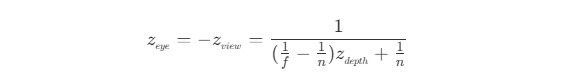
- 当相机位置为 0 ,远裁剪平面为 1 时,即在左手坐标系下整体缩小
f,则深度值z_linear01为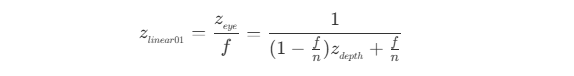
- 当近裁剪平面为 0 ,原裁剪平面为 1 时,即在左手坐标系下先移动
-n,再整体缩小f,则深度值z_linear01FromNear为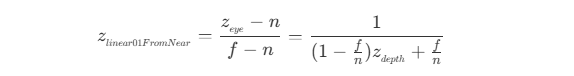
- 因此,用于在 shader 中计算深度的
_ZBufferParams参数值为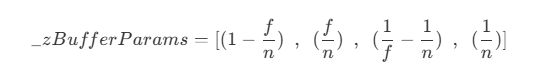 在
在 com.unity.render-pipelines.core/ShaderLibrary/Common.hlsl中,获取线性深度的方法为
// Common.hlsl
...
// Z buffer to linear 0..1 depth (0 at near plane, 1 at far plane).
// Does NOT correctly handle oblique view frustums.
// Does NOT work with orthographic projection.
// zBufferParam (UNITY_REVERSED_Z) = { f/n - 1, 1, (1/n - 1/f), 1/f }
// zBufferParam = { 1 - f/n, f/n, (1/f - 1/n), 1/n }
float Linear01DepthFromNear(float depth, float4 zBufferParam)
{
#if UNITY_REVERSED_Z
return (1.0 - depth) / (zBufferParam.x * depth + zBufferParam.y);
#else
return depth / (zBufferParam.x * depth + zBufferParam.y);
#endif
}
// Z buffer to linear 0..1 depth (0 at camera position, 1 at far plane).
// Does NOT work with orthographic projections.
// Does NOT correctly handle oblique view frustums.
// zBufferParam (UNITY_REVERSED_Z) = { f/n - 1, 1, (1/n - 1/f), 1/f }
// zBufferParam = { 1 - f/n, f/n, (1/f - 1/n), 1/n }
float Linear01Depth(float depth, float4 zBufferParam)
{
return 1.0 / (zBufferParam.x * depth + zBufferParam.y);
}
// Z buffer to linear view space (eye) depth.
// Does NOT correctly handle oblique view frustums.
// Does NOT work with orthographic projection.
// zBufferParam (UNITY_REVERSED_Z) = { f/n - 1, 1, (1/n - 1/f), 1/f }
// zBufferParam = { 1 - f/n, f/n, (1/f - 1/n), 1/n }
float LinearEyeDepth(float depth, float4 zBufferParam)
{
return 1.0 / (zBufferParam.z * depth + zBufferParam.w);
}
...
总结
- 计算机图形学中,变换的应用非常多,渲染时基本上离不开坐标变换,理解各个过程的变换矩阵,也有助于理解整个渲染的过程。