Graphics

图形学篇 — 阴影

Posted by Xun on Wednesday, April 5, 2023

真实世界中，伴随着光的存在，阴影也会同步出现。因此图形学中，为了让物体看起来更加真实，阴影是不可或缺的。

简介

  • 阴影（Shadow），由全影（umbra）和半影（penumbra）组成。
    • 全影：拥有完全阴影的区域
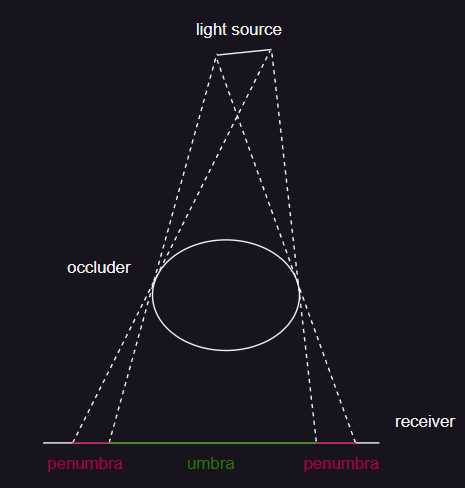
    • 半影：拥有部分阴影的区域 Shadow_1.png
  • 硬阴影（Hard Shadow）：只有全影区域，边界锐利的阴影。
  • 软阴影（Soft Shadow）：全影区域和半影区域同时存在的边界柔和阴影，当光源为区域光时产生。

阴影图（Shadow Map）

  • 1978年，Williams 提出了一种基于 z-buffer 的通用渲染方法，可以用于在任意对象上快速生成阴影。核心思路是：
    • 从产生阴影的光源位置出发，渲染整个场景，能被看到的地方则能被照亮，不能被看到的地方即为阴影。生成阴影图的时候，仅需要 z-buffer ，光照、纹理、颜色缓冲写入都可以关闭。此时，z-buffer 中的每个像素记录了光源和最靠近的场景对象的深度值 z。
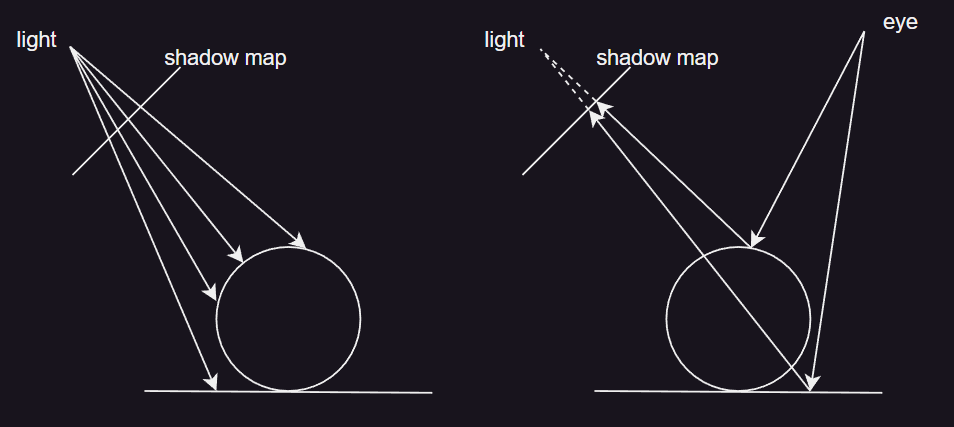
    • 从观察者的角度出发，再次渲染整个场景。每一个对象所在的像素，都要和阴影图比较。如果该像素到光源的距离比阴影图中记录的距离远，则该像素处在阴影中。 Shadow_2.png
  • Shadow Map 是非常流行的算法，因为其是相对可预测的。构建阴影图的成本，与渲染图元的数量大致呈线性关系，并且访问时间是恒定的。当场景的光源和物体没有移动时，阴影图可以只生成一次，每一帧都反复使用。
  • 而 Shadow Map 的缺点，就是阴影的质量取决于阴影图的分辨率 (以像素为单位) 和 z-buffer 的数值精度。
    • 如果想要高精度的阴影，则需要使用较高的分辨率和精度，但相对地就需要占用更大的内存。
    • 如果要限制内存占用，则需要牺牲阴影的精度，即可能出现混叠等问题。

阴影粉刺（Shadow Acne）

  • 由于阴影图是在深度比较期间采样的，因此该算法容易出现混叠问题，尤其是靠近对象之间的接触点。一个常见的问题是自阴影混叠，通常叫 surface acne 或 shadow acne，即三角面被错误认为是阴影。产生此问题的原因有两个：
    • 处理器精度的数值极限问题。
    • 采样点的值代表的是一个区域的深度值，从光源出发的采样点，几乎不会和从观察方向出发的采样点相同。

斜率比例偏差（Slope Scale Bias）

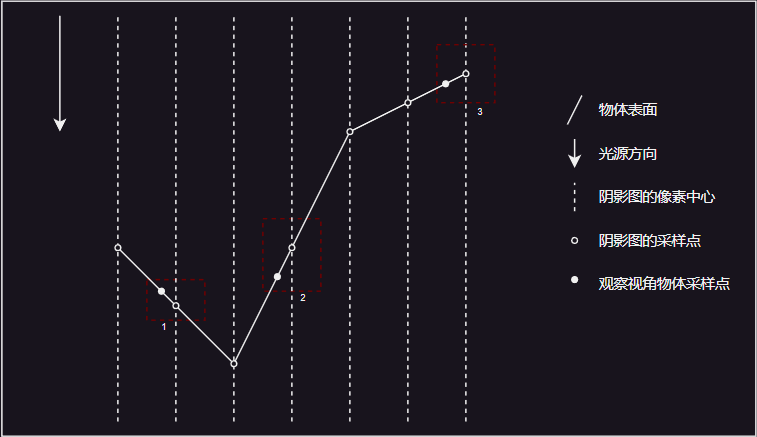
Shadow_3.png

  • 可以看到，区域1中物体表面的点的深度比阴影图的采样点深度小（距离光源更近），因此能被正常照亮，而区域2、3中点的深度，则比阴影图的采样点深度大，因此被错误地认为是在阴影中，因为比较时取了阴影图另一个点的深度来比较。
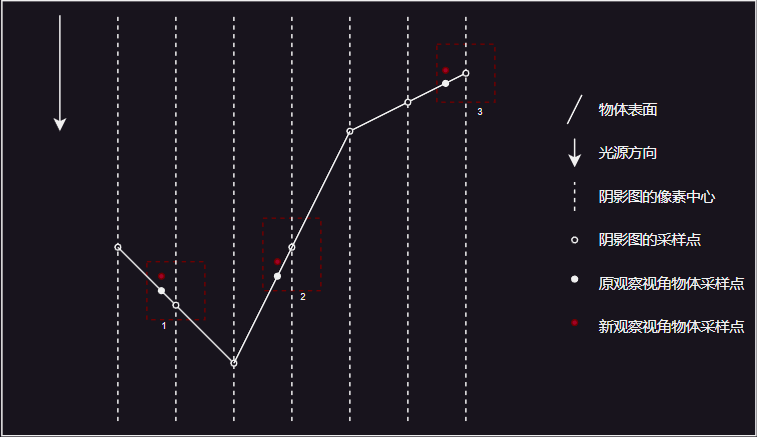
  • 为了避免出现 shadow acne 问题，一个常用的方法是引入偏差因子，即当物体的深度与阴影图进行比较前，先对物体深度减去一个小的偏移量后，再进行比较。 Shadow_4.png
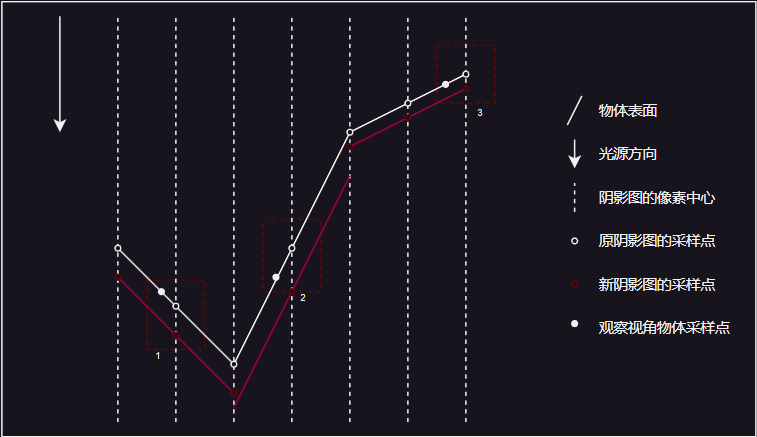
  • 然而，如果接收阴影的物体表面和光源越趋于平行时，使用常量的偏移量则容易出现错误。如上图中使用了常量的偏移量，区域1、3能正常被照亮，但区域2仍然会处于阴影中。 Shadow_5.png
  • 另一种更有效的方法是，通过物体表面和光源的角度来设置阴影图的偏移量，阴影图的深度会加上这个偏移量后再进行比较。表面与光源越接近平行，偏移量就越大，从而避免问题。这种类型的偏差即为斜率比例偏差。
  • 当物体表面和光源接近垂直时，斜率比例偏差几乎为 0，因此一般需要将常量偏差和斜率比例偏差一起使用，来避免出现混叠问题。

法线偏移偏差（Normal Offset Bias）

  • 法线偏移偏差，是通过将采样点沿着物体表面法线方向偏移，偏移量与法线和光源之间的角度的正弦成正比。对于中心样本，这可以被认为是移动到原始表面上方的假想表面。这种偏差不仅会影响深度，还会更改用于阴影图测试的纹理坐标。

Peter 平移（Peter Panning）

  • 当偏移量太大时，会导致一个称为 light leaks 或 Peter Panning 的问题，即物体看起来会稍微高于下表面。因为物体接触点下方的区域被推得太远，导致比较深度后不能接收到阴影。
  • 因此，偏移量的选择需要根据实际情况进行调整。

PCF（Percentage-Closer Filtering）

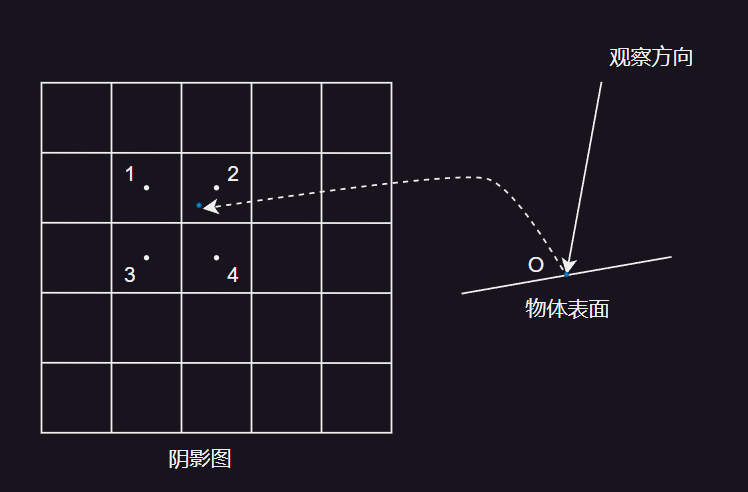
  • PCF 是 Shadow Map 的一个扩展，可以用于产生伪软阴影，也可以用于改善由于分辨率不足引起的块状阴影问题。 Shadow_6.png
  • 如图所示，PCF 的流程为
    • 对于物体表面的点，找到到阴影图中的对应点。
    • 对阴影图中的点，找到相邻的四个像素点，对阴影图进行采样。
    • 对每个采样得到的深度结果，和物体表面的深度进行比较，用 0 表示阴影，1 表示光照。
    • 将所有比较结果进行双线性插值，得到光源最终在物体表面的作用量。
  • 采样、修改附近的阴影图位置，有很多不同的选择，包括采样的面积有多宽，要使用多少样本，采样模式以及如何对结果进行加权等。
  • PCF 是非物理的处理方式。因为在真实物理世界中，软阴影的大小会受遮挡物体和接收物体的距离影响，而 PCF 只会从着色点映射到阴影图进行采样，与遮挡物体的距离并不会影响的阴影大小，因此最终会得到几乎相同的软阴影区域。
  • 然而，自阴影问题，以及前面提到的 Shadow Acne 和 Peter Panning 问题，在 PCF 下会表现得更加糟糕。例如，原本使用 Slope Scale Bias 的时候，阴影图会根据物体表面斜率将表面往远离光源的方向偏移，从而采样点能正常照亮。而当 PCF 在阴影图较大范围采样时，得到的结果可能由非阴影变成阴影，即出现自阴影问题。
  • 为了解决自阴影问题，需要通过使用常数偏移、斜率比例偏差、接收平面、视图偏差、法线偏差的组合，但仍然需要对根据不同的环境进行手动调整。

PCSS（Percentage-Closer Soft Shadows）

  • 尽管 PCF 能产生软阴影，但是遮挡物体的和光源的距离并不会影响的阴影大小，因此软阴影的大小基本是相同的。在此基础上，Fernando 提出了 Percentage-Closer Soft Shadow（PCSS）方法，主要包括三个步骤：
    • 遮挡物查找。
    • 半影尺寸估算。
    • 可变的 PCF 处理。

遮挡物查找

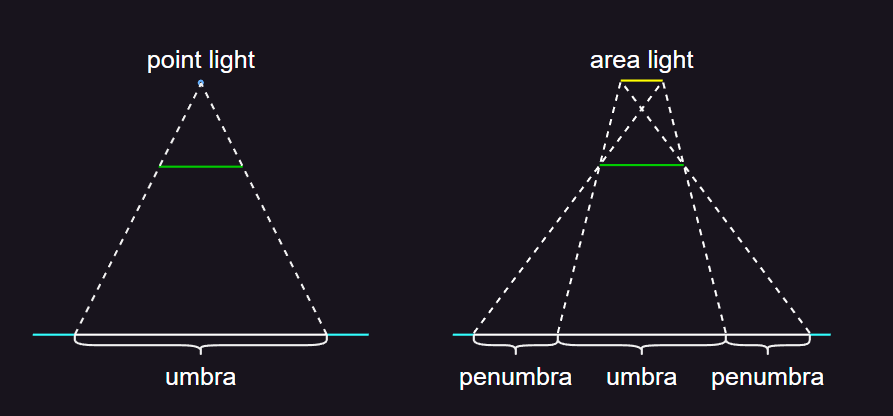
PCSS_2.png

  • 从图中可以发现，点光源只能产生全影区域，而半影区域需要区域光产生。
  • 当光源为点光源时，每一个着色点，只有一个点光源对其产生作用，映射到阴影图上的一个点，比较深度后确定是否处在阴影中，通过 PCF 方法，来生成软阴影。
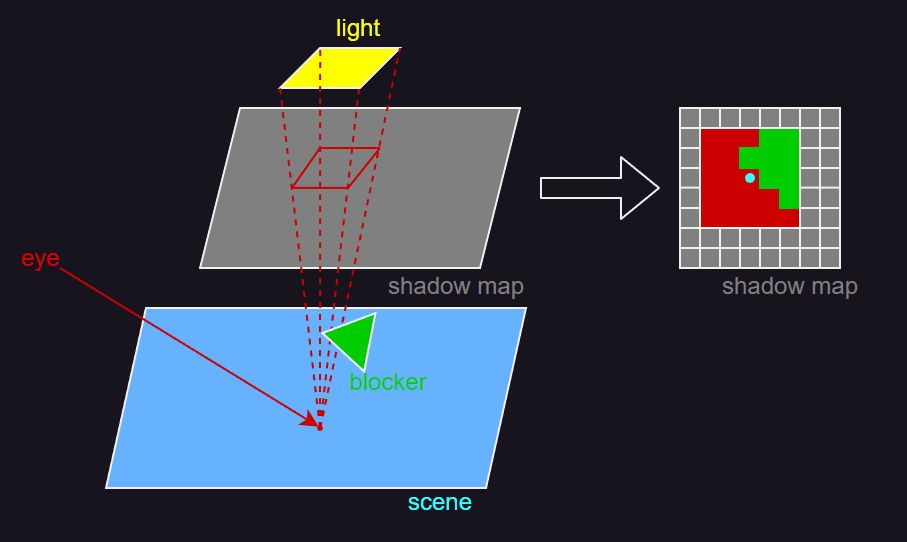
  • 而当光源为区域光时，从光源中心出发产生阴影图，每一个着色点，有一片区域光对其产生作用，映射到阴影图上。阴影图上的采样区域大小，受光源大小、接收物体和光源的距离影响。 PCSS_3.png
  • 可以看到，从光源出发，到场景点的所有遮挡物区域，即阴影图这个区域中深度比着色点的深度小的像素点，即右侧阴影图的绿色点。

半影尺寸估算

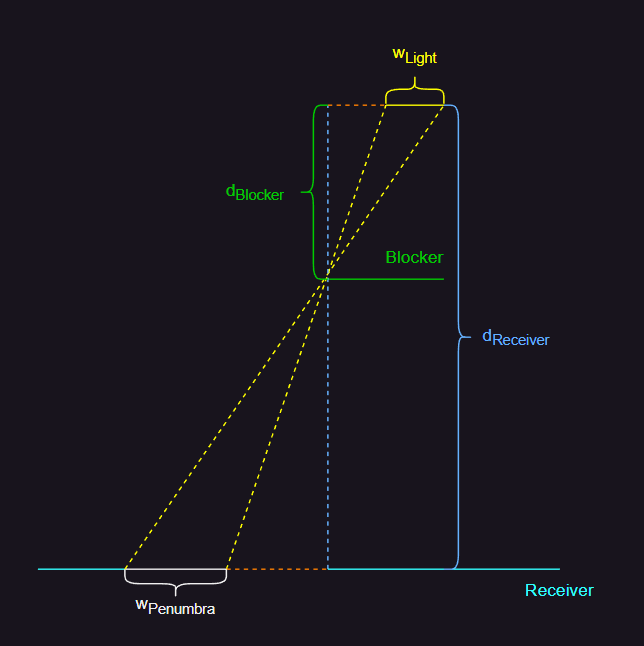
PCSS_1.png

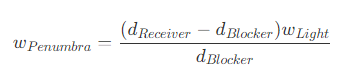
  • 从上图可以得到，半影的大小和光源大小、光源到接收面的距离、光源到阻挡物的距离有关，可以表示为 Math_Shadow_1.png
  • 为了得到半影的尺寸，需要的参数有
    • 接收物到光源的距离。
    • 遮挡物到光源的距离。
    • 光源大小。
  • 其中，光源大小一般是已知的，可以通过 shader 统一的输入获得。而接收物到光源的距离，也就是该点在光源下的深度，也可以直接计算得到。而遮挡物到光源的距离，不能直接得到。
  • 遮挡物在阴影图上为一个区域，如果直接取其中的最小值，则会受最小值的所在位置影响，导致可能出现伪阴影。通常需要对阴影图上所有遮挡物的深度求平均值，来作为遮挡物到光源的距离。
  • 至此，所有需要的参数都已经得到，则半影的尺寸可以估算出来。

可变的 PCF 处理

  • 常规的 PCF ，对各个点都采用相同的内核进行滤波。而可变的 PCF 内核则可以使用变化的滤波范围，以及不同数量的采样点。通过上一个步骤，可以估算出来每个点对应的半影尺寸，因此会基于每个结果来确定每个点执行 PCF 使用的内核参数。
  • 通过估算得到半影大小后，为了优化性能，可以选择只有存在半影时，才进行 PCF 处理，则省去了全影和完全光照区域的多余计算过程。

VSM（Variance Shadow Mapping）

  • PCF 中，计算着色点的阴影时，需要对阴影图的多个样本点进行采样，来得到着色点的光照量，即非阴影的占比。然而，当使用较大范围的采样区域和较多的样本点，对一个着色点进行处理时，会有较大的性能压力。

切比雪夫不等式

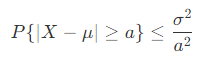
  • 切比雪夫不等式指出，对于随机变量 X ，其有限期望为 E(X) = μ ，有限方差 D(X) = σ^2 ，则对任意 a ＞ 0，变量 X 在 [-∞, -μ - a] 和 [μ + a, +∞] 范围的概率 P 满足 Math_Shadow_2.png
  • 也就是说，对一批离散数据，在某个范围内的样本数量占比，可以通过该不等式直接估算出来。

单边的切比雪夫不等式

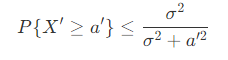
  • 单边切比雪夫不等式，可以由马尔科夫不等式推导得到。单边的切比雪夫不等式指出，对于随机变量 X' = X - μ ，期望为 E(X') = E(X - μ) = 0 ，有限方差 D(X') = D(X - μ) = σ^2 ，则对任意 a' ＞ 0 ，变量 X' 在 [a', +∞] 范围的概率 P 满足 Math_Shadow_3.png
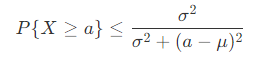
  • 可以看出，单边不等式是对将原数据减去期望值后得到的关系，即求 X' ≥ a' 范围的概率，就是求 X ≥ a' + μ 范围的概率。因此求 X ≥ a 的范围，即 a = a' + μ ，则不等式可以表示为 Math_Shadow_4.png

阴影应用

  • 对应到 PCF 中，X 即为阴影图上滤波区域的深度值，a 即为着色点在光源下的深度值，P 即为未被遮挡（a ≤ X）的占比，也就是 PCF 计算需要的结果。
  • 然而，P 是一个上界，而 PCF 需要得到一个具体值，当满足某些条件时，可以取最大值为最终结果。
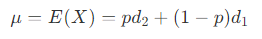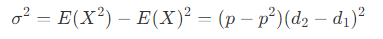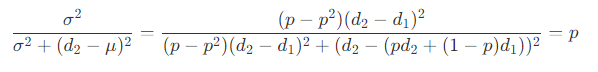
  • 当光源通过一个深度为 d1 的平面遮挡物，在深度为 d2 的平面接收物上产生阴影，设 p 为未被遮挡的概率，由于遮挡物只有一个，且为平面，因此在小范围内，遮挡的区域深度都为 d1 ，未被遮挡的区域都为 d2 ，则期望 μ 为 Math_Shadow_5.png 方差 σ^2 为 Math_Shadow_6.png 此时未被遮挡的范围，即 X ≥ d2 ，则 P 的上限值为 Math_Shadow_7.png
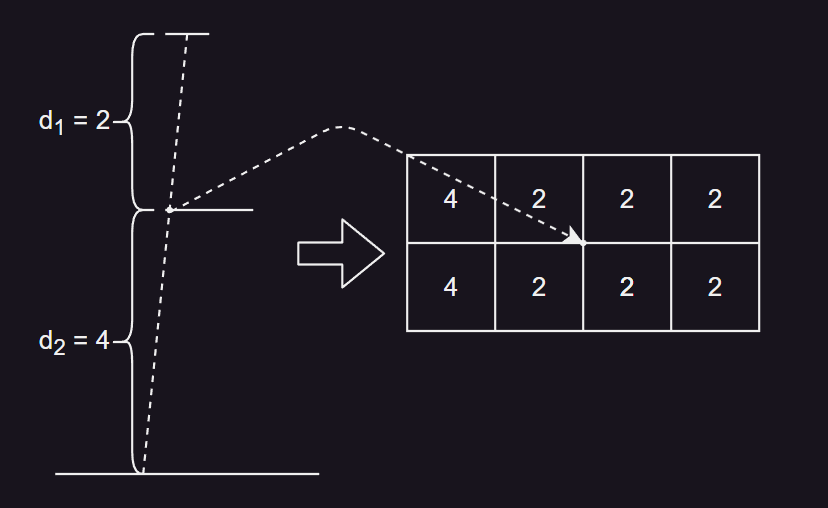
  • 此时上限值即为未被遮挡的概率，即可以直接用上限值来估算。 VSM_1.png
  • 如上图示例，未被遮挡的点，即为阴影图采样区域中，深度不小于 4 的值，则 PCF 计算占比为 2/8 = 0.25 。采样区域期望为 2.5 ，方差为 0.75 ，则根据单边切比雪夫不等式估算的上限值为 0.75/(0.75 + (4 - 2.5)^2 = 0.25 ，和 PCF 估算值一致。
  • 尽管有一定的使用条件，但通常都会使用上限值来作为 PCF 的简化计算，一般都能得到较好的表现结果。

SAT（Summed-Area Table）

  • 使用单边的切比雪夫不等式估算时，都需要获得每个点在阴影图上某个范围内的期望和方差值，而期望和方差可以通过 Mipmap 或 SAT 方式来快速获得。
  • 对阴影图构建对应的 Mipmap 纹理后，当查找某个点的期望时，能够直接从图上采样得到，速度很快，然而也有一定的不足：
    • 需要正方形区域。
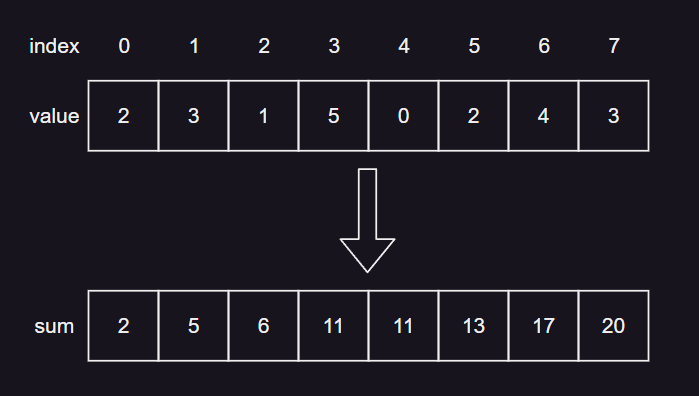
    • 只能生成多级纹理，如果在两级之间的，即便使用三线性插值来获取，也只能获得近似值。 SAT_1.png
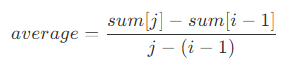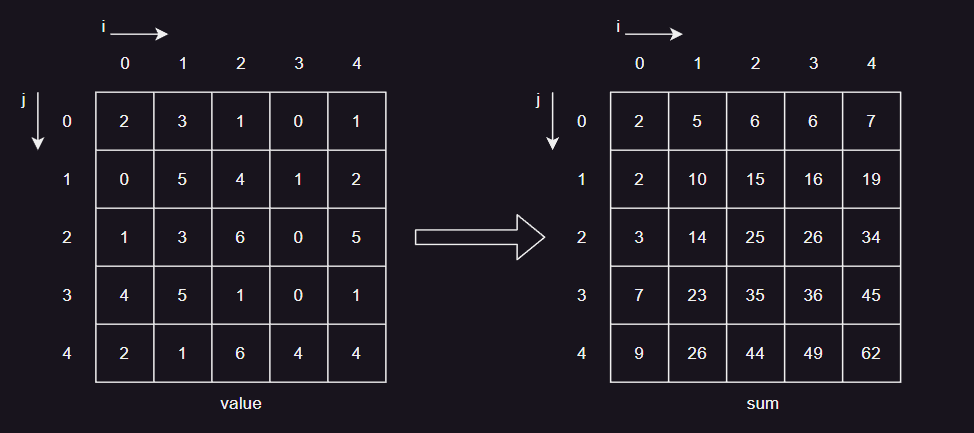
  • 如图所示，value[index] 为原始数据，sum[index] 为 value[0] ~ value[index] 的和。当需要求 value[i] ~ value[j] 的平均值时，则 Math_Shadow_8.png 即原本算法需要 O(n) ，使用 SAT 后只需要 O(1) 即可得到。 SAT_2.png
  • 对于二维数据，当需要求 value[left, right] ~ value[top, bottom] 的平均值时，则 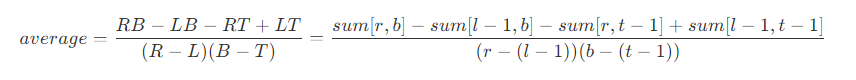Math_Shadow_9.png 即只需要知道左上、左下、右上、右下的值，就可以在 O(1) 内得到平均值。
  • 阴影图记录了光源下每个像素的深度值，需要增加一张图记录每个像素的深度平方值，通过分别构建 SAT 数据，即能在 O(1) 时间内得到 PCF 的结果。
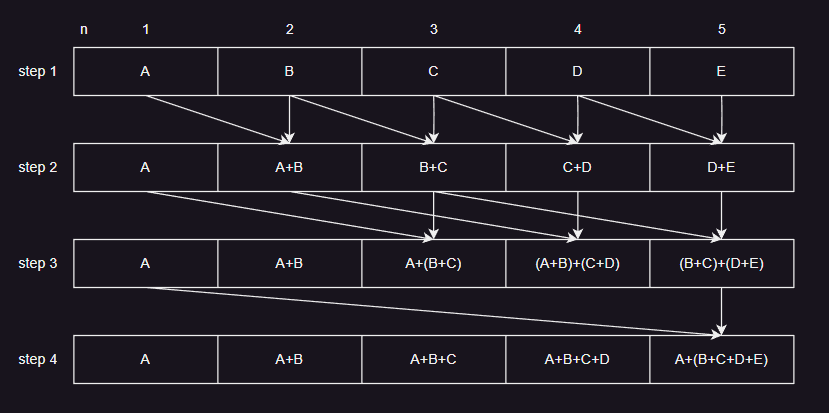
  • 对于 SAT 数据的构建，通常需要一次遍历，即时间复杂度为 O(n) 。在 GPU 生成时，由于需要依赖前一个数据，因此需要 n 个 pass 。 SAT_3.png
  • Justin Hensley 提出了加速算法，如上图所示，主要步骤为：
    • 第 1 步，将每个像素的值，加上左边第 1 个像素的值，此时每个像素为 2 个数据的和。
    • 第 2 步，将每个像素的值，加上左边第 2 个像素的值，此时每个像素为 4 个数据的和。
    • 第 3 步，将每个像素的值，加上左边第 4 个像素的值，此时每个像素为 8 个数据的和。
    • 第 k 步，对每个像素的值，加上左边第 2^(k - 1) 个像素的值，此时每个像素为 2^k 个数据的和。
    • 重复以上步骤，直到每个像素为 n 个数据的和。
  • 此加速算法充分利用了 GPU 并行计算的优势，对于一维的 n 个数据，只需要 O(log n) 时间即可完成 SAT 数据的构建。对于二维数据，只需要先进行一次横向处理，再进行一次竖向处理，即可得到 SAT 数据。

VSSM（Variance Soft Shadow Mapping）

算法介绍

  • 在 PCSS 中，第三步使用 PCF 计算，可以使用 VSM 来优化计算，然而第一步查找遮挡物，同样需要采样阴影图中的一个区域，来找到被遮挡部分的平均深度。定义
    • X ：阴影图上滤波区域的深度值。
    • a ：着色点在光源下的深度值。
    • z_unocc ：滤波区域中 X ≥ a 的所有样本点的平均深度。
    • z_occ ：滤波区域中 X ＜ a 的所有样本点的平均深度。
    • z_avg ：滤波区域所有样本点的平均深度。
    • N ：滤波区域的样本点数量。
    • N_unocc ：滤波区域中 X ≥ a 的样本点数量。
    • N_occ ：滤波区域中 X ＜ a 的样本点数量。
    • P ：滤波区域中 X ≥ a 的比例。
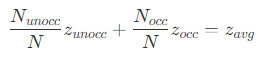
  • 则有以下关系 Math_Shadow_10.png
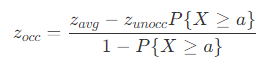
  • 可以得到 z_occ 的表示 Math_Shadow_11.png
  • 同样假设遮挡物和接收物都为平面，则未被遮挡的平均深度 z_unocc 即为着色点深度 a ，通过 VSM 可以得到阴影图的平均深度 z_avg ，以及未被遮挡的区域占比 P ，因此平均深度同样可以在 O(1) 时间内得到，从而计算效率得到较大的提升。

非平面性问题

  • 单边切比雪夫不等式中要求，a' = a - μ ＞ 0 ，即 a ＞ z_avg ，不等式才能成立。当遮挡物和接收物都为一个平面时，能满足这个关系。然而当出现非平面性的问题，即有多个遮挡物、多个接收物等情况，出现 a ≤ z_avg 时，会出现漏光的问题，即在本应该无光照的区域出现了光照效果。尽管通过在更小范围内使用更多采样点，能解决这个问题，但就会回到 PCF 计算带来的性能问题。因此，需要引入滤波器内核细分方案来处理非平面性问题。
  • 当 a ≤ z_avg 时，表示着色点没有被遮挡，即光照计算结果为 1 。当滤波内核 w 较小时，即滤波区域较小时，阴影图区域内的绝大部分像素深度值都比着色点深度大，因此能认为都没有被遮挡。随着内核 w 逐渐增大，平均深度的误差会越来越大，因此会出现错误的结果。因此需要使用较小的滤波内核，即解决步骤为：
    • 将滤波内核划分成更小的子内核 w'。
    • 子区域中，如果 a ＞ z'_avg ，则可以使用单边切比雪夫不等式计算。
    • 子区域中，如果 a ≤ z'_avg ，则有两种处理方式：
      • 认为子区域中所有像素都未被遮挡。
      • 使用常规 PCF 采样，进行阴影测试。
  • 由于内核足够小，因此对于 a ≤ z'_avg 的第一种处理方式能够成立，这种处理方式也符合 VSM 的思路。同样，在小内核下，第二种方式能以很低的性能消耗进行 PCF 2x2 采样来得到非常准确的结果。因此第二种方式也经常被使用。
  • 对于内核的细分，有均匀细分和自适应细分方案。
    • 均匀细分：将区域切分成均等大小的子区域，子区域分为常规组和非平面组。计算平均遮挡深度时采用 m x m 的内核，计算软阴影时采用 n x n 的内核。当 m 为 5 时能得到较好的表现，而 n 通常要比 m 大。
    • 自适应细分：通过构建四叉树，将区域进行划分，如果子区域 a ＞ z'_avg ，则不需要再划分。如果 a ≤ z'_avg ，则此子区域需要继续划分，直到子区域的方差小于阈值，经过测试，阈值一般定位 0.0001r，其中 r 为输入场景球形包围盒的半径。 VSM_2.png

局限性

  • 当数据出现多个峰值时，用正态分布来描述数据会不准确，此时使用 VSM 或 VSSM 进行阴影估计时，得到的结果则不准确。可以使用 MSM（Moment Shadow Mapping）来改善，即使用更高阶的矩（moment）。VSM 和 VSSM 使用二阶矩（方差）来描述数据的分布情况，对正态分布的数据则能得到较好的结果。对于其他数据情况，使用越高的矩则越能准确描述出数据的分布情况。通常情况下，使用四阶矩就足够近似得到数据分布情况。

DFSS（Distance Field Soft Shadow）

  • DFSS 不是基于 Shadow Mapping 的方法，而是在着色点和光源的连线上，通过 SDF 查找每个点与遮挡物的最小距离，得到安全角度，从而计算出着色点的光照量。

SDF

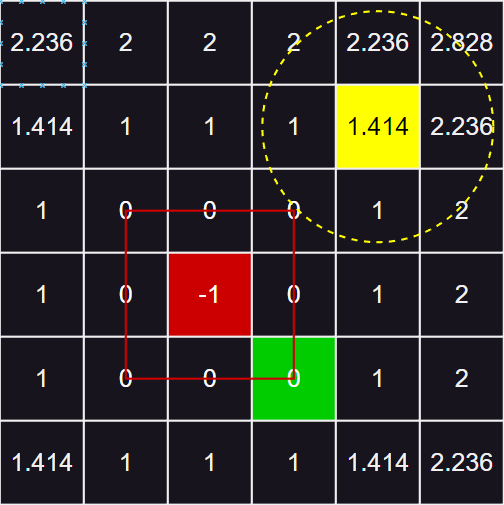
  • SDF（Signed Distance Filed），有向距离场，即场景中所有点都有一个距离值，表示到最近的物体表面的距离。其中，物体表面外的点为正数，物体内部的点为负数，物体表面上的点则为 0 。 DFSS_1.png
  • 如上图所示，在 2D 平面上，边长为 1 红色正方形边框为场景物体，红色格子为物体内部，则到表面的最小距离为 -1 ，绿色格子在物体表面，则距离为 0 ，黄色格子在物体外面，则距离为正。3D 场景类似。
  • 关于如何构建 SDF ，可以参考 算法篇 — EDT 欧式距离变换 。
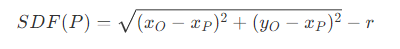
  • 场景中的单个物体同样可以用 SDF 来表示，如圆心为 O 、半径为 r 的圆距离函数可以表示为： Math_Shadow_12.png
  • 其中，P 为任意一点，则距离为 P 到 O 的距离与半径的差值（圆内为负数，圆上为 0 ，圆外为正数）。
  • 每个物体（刚体）都可以具有各自的 SDF 距离函数，因此如果要知道场景中某个点距离最近的物体，只需要以该点查找所有物体的 SDF 函数，其中距离最小对应的物体即为目标物体。

Ray marching(Sphere tracing)

  • 步进式光线追踪，即从某个点出发，通过查找 SDF 得到该点离物体的最小距离，以该点为圆心可以构建出一个圆，这个圆代表安全范围，即圆内不会有其他物体。沿着光源的方向，与圆有一个交点，将交点作为新的起点，重复前面的步骤，直到抵达物体表面。 DFSS_2.png

应用

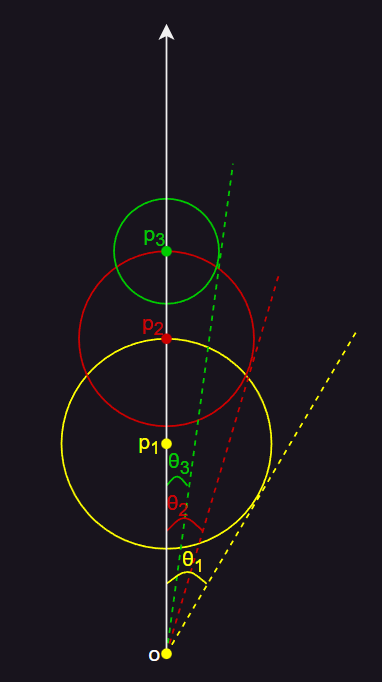
DFSS_3.png

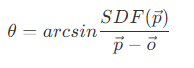
  • 在 Ray marching 过程中，每一步都会产生一个安全范围圆，从着色点 o 出发，找到与圆的切线，得到一个安全角度 θ ，即光源面到着色点不被遮挡的角度。如果最后不能达到光源，则说明被遮挡了。如果到达光源了，则所有安全角度中，最小的角度即为着色点对光源最终的安全角度，即在这个角度内的所有光照都不会被遮挡，如果超过这个角度，则会有部分光照被遮挡。安全角度可以表示为 Math_Shadow_13.png
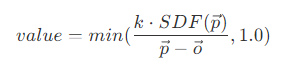
  • 在 shader 中反三角函数的计算比较复杂，Inigo Quilez 指出，从着色点朝光源发出的阴影射线与遮挡物的最近交点，如果越靠近阴影射线，或者越靠近着色点，则着色点的阴影越深，因此提出了着色点的光照计算公式： Math_Shadow_14.png
  • 其中，k 用于控制半影区域的大小，当 k 越大时，则被完全照亮的区域越大，即半影区域越小。其他参数都可以在 Ray marching 过程中得到，因此通过此方法计算阴影可以有非常高的效率。
    DFSS_4.png
    引自 https://iquilezles.org/articles/rmshadows/

改进方案

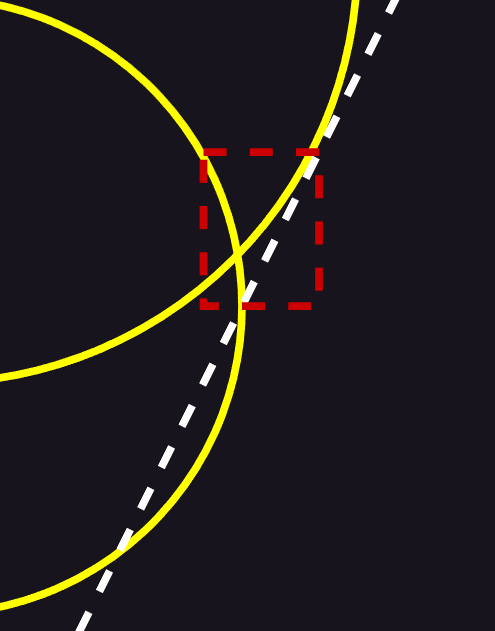
DFSS_5.png

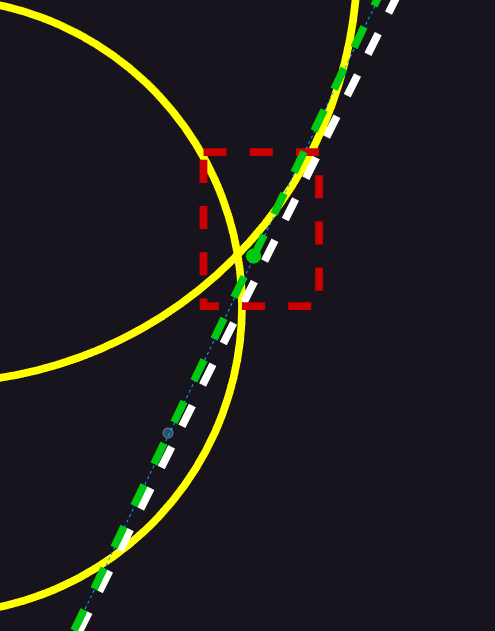
  • 在步进的过程中，安全角度通过圆的切线可以得到，如上图白色虚线所示，代表在白色虚线以内的范围内光不会被遮挡。 DFSS_6.png
  • 事实上，步进过程只能保证圆内没有任何阻挡，从上图红色框中可以看到，白色虚线以内有一小部分区域并不在圆内，假设图中绿色点处有遮挡物，则在原来的算法上，这个遮挡物也会被正常照亮，从而出现错误表现。也就是说，最小安全角度不再是白色虚线的角度，应该为绿色虚线的角度。
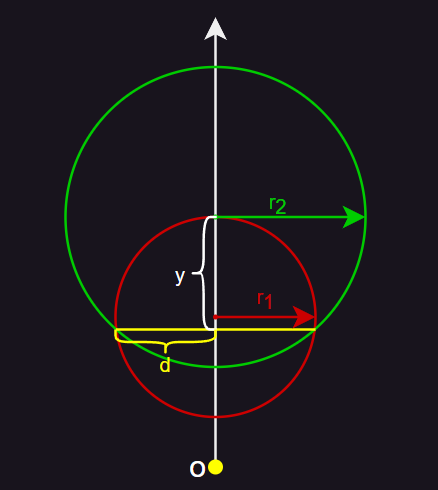
  • 在 DFSS 方案提出的七年后，Sebastian Aaltonen 提出了一个改进方案，即在步进的过程中，可以估算最近的遮挡点在两个圆的交点附近。其中，d 为两个圆交点连线距离的一半，y 为当前圆心到两圆交点连线的距离。 DFSS_7.png
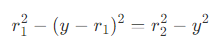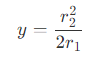
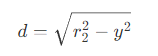
  • 由图中可以得到关系 Math_Shadow_15.png 则可以得到 Math_Shadow_16.png Math_Shadow_17.png
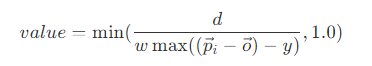
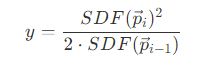
  • 而改进后的算法则为 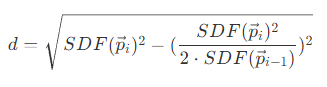Math_Shadow_18.png Math_Shadow_19.png Math_Shadow_20.png 其中，w 表示光源大小（立体角）。
  • 改善后的效果如下
    DFSS_8.png
    引自 https://iquilezles.org/articles/rmshadows/
  • Inigo Quilez 还提出了另外的优化方案，即步进过程，当到达物体表面时，会继续往前延伸，直到阴影真正变暗（即光照结果为 -1），通过这种调整，最终的 SDF 阴影看起来非常接近物理上正确的效果，如图所示
    DFSS_9.png
    引自 https://iquilezles.org/articles/rmshadows/
    DFSS_10.png
    引自 https://iquilezles.org/articles/rmshadows/

总结

  • 阴影是渲染中非常重要的一个技术，对于呈现更加真实的画面来说至关重要。Shadow Mapping 技术，基于其概念简单以及实现方便，目前仍然是使用相对普遍的技术。而 SDF 类的技术，在某些情况下也有优于 Shadow Mapping 的表现和性能。阴影的实现方式有很多，简单的可以是统一的圆底，复杂的可以是实时阴影，需要根据不同的项目需求，来选择适合的实现方式。

参考文献

CATALOG