简介
深度值
- 透视投影经过齐次除法后,
z_NDC 的值为
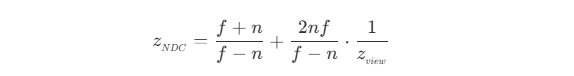
- 在像素着色器中,每一个像素的坐标都需要通过插值计算得到,在透视投影下,需要使用透视校正插值。此时,如果深度图使用观察空间下的
z_view ,则在插值过程需要对属性 I 除以 z_view 计算,因此深度图使用 z_NDC 可以减少计算复杂度。
- 由于深度图的范围为
[0, 1] ,因此深度图中的 z_depth 值为
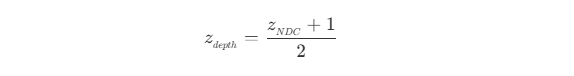
- 可以看到,齐次除法后的
z_NDC 值已经不为观察空间下 z_view 值的线性变换,因此使用深度图的深度信息时,需要变换观察空间下才能进行其他计算,即
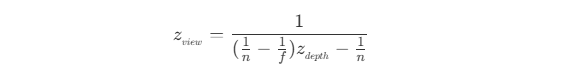
- 由于 OpenGL 中观察空间为右手坐标系,而裁剪空间下是左手坐标系,所以观察空间下的
z_view 值需要取反,才为左手坐标系下的线性 z_eye 值,即
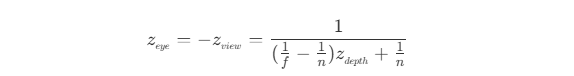
- 当相机位置为 0 ,远裁剪平面为 1 时,即在左手坐标系下整体缩小
f ,则深度值 z_linear01 为
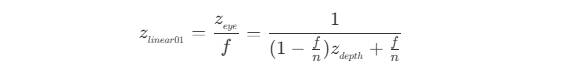
- 当近裁剪平面为 0 ,原裁剪平面为 1 时,即在左手坐标系下先移动
-n ,再整体缩小 f ,则深度值 z_linear01FromNear 为
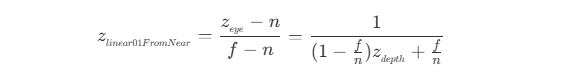
- 因此,用于在 shader 中计算深度的
_ZBufferParams 参数值为
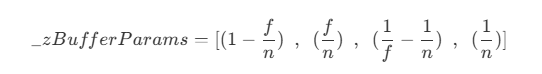 在
在 com.unity.render-pipelines.core/ShaderLibrary/Common.hlsl 中,获取线性深度的方法为
// Common.hlsl
...
// Z buffer to linear 0..1 depth (0 at near plane, 1 at far plane).
// Does NOT correctly handle oblique view frustums.
// Does NOT work with orthographic projection.
// zBufferParam (UNITY_REVERSED_Z) = { f/n - 1, 1, (1/n - 1/f), 1/f }
// zBufferParam = { 1 - f/n, f/n, (1/f - 1/n), 1/n }
float Linear01DepthFromNear(float depth, float4 zBufferParam)
{
#if UNITY_REVERSED_Z
return (1.0 - depth) / (zBufferParam.x * depth + zBufferParam.y);
#else
return depth / (zBufferParam.x * depth + zBufferParam.y);
#endif
}
// Z buffer to linear 0..1 depth (0 at camera position, 1 at far plane).
// Does NOT work with orthographic projections.
// Does NOT correctly handle oblique view frustums.
// zBufferParam (UNITY_REVERSED_Z) = { f/n - 1, 1, (1/n - 1/f), 1/f }
// zBufferParam = { 1 - f/n, f/n, (1/f - 1/n), 1/n }
float Linear01Depth(float depth, float4 zBufferParam)
{
return 1.0 / (zBufferParam.x * depth + zBufferParam.y);
}
// Z buffer to linear view space (eye) depth.
// Does NOT correctly handle oblique view frustums.
// Does NOT work with orthographic projection.
// zBufferParam (UNITY_REVERSED_Z) = { f/n - 1, 1, (1/n - 1/f), 1/f }
// zBufferParam = { 1 - f/n, f/n, (1/f - 1/n), 1/n }
float LinearEyeDepth(float depth, float4 zBufferParam)
{
return 1.0 / (zBufferParam.z * depth + zBufferParam.w);
}
...
Reversed-Z 优化
- 由于
z_NDC 是按 1/z_view 关系分布的,因此,z_NDC 区间的绝大部分值,都映射到接近近裁剪平面附近,精度较高,而靠近远裁剪平面部分,z_NDC 的变化很小,精度较低,即在较大区间范围内的所有 z_view 都对应同一个 z_NDC 值,因此容易出现 z-fighting 问题。而在近裁剪平面附近,通常也不需要这么高的精度。
- 在 D3D 中,
z_NDC 的范围为 [0, 1] ,对应 z_view 的 [near, far] ,而深度值通常使用 4 bit 来存储浮点数。根据浮点数的量化规则,当浮点数越接近 0 时,同样位数的存储能有更大的精度,即能表示更小的浮点数,但这些值对应的 z_view 变化范围非常小。如果将深度值按 1 - z_NDC 存储,即远裁剪平面对应 z_NDC 为 0,利用浮点数的特点,可以在靠近远裁剪平面获得更大的精度,一定程度上抵消非线性深度的问题,这种方式称为 Reversed-Z。
- 然而,在 OpenGL 中,由于
z_NDC 的范围为 [-1, 1] ,浮点数的高精度部分集中在中间区域,远裁剪平面无法通过使用 Reversed-Z 优化。尽管 z_NDC 在后续会将值映射到 [0, 1] 存入深度图,但由于初始映射到 [-1, 1] 的过程已经破坏了远裁剪平面部分的精度,所以 Reversed-Z 作用不大。
计算观察坐标
总结
- 计算机图形学中,变换的应用非常多,渲染时基本上离不开坐标变换,理解各个过程的变换矩阵,也有助于理解整个渲染的过程。此外,由于变换过程中对深度产生影响,了解其中的原理,也能更好地理解深度图相关的各个参数和公式的含义。
参考
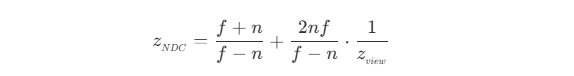
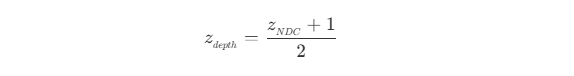
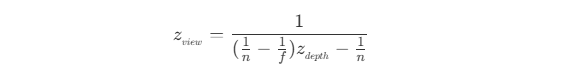
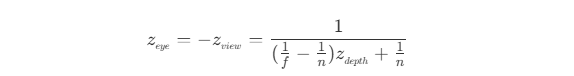
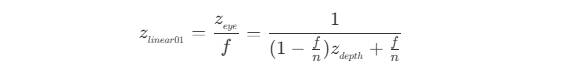
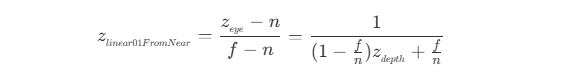
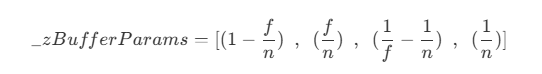 在
在