贝塞尔曲线是计算机图形中常用的绘制曲线的方法，能根据多个点的位置绘制出光滑的曲线。
简介
- 在计算机中，要绘制一条曲线，并不像手绘一样方便，通过鼠标来绘制往往很难绘制出光滑的、令人满意的曲线。而贝塞尔曲线，即可以通过几个给定的控制点，绘制出唯一的一条光滑的曲线，从而很大程度上弥补了计算机图形中的这一不足。
几何表示
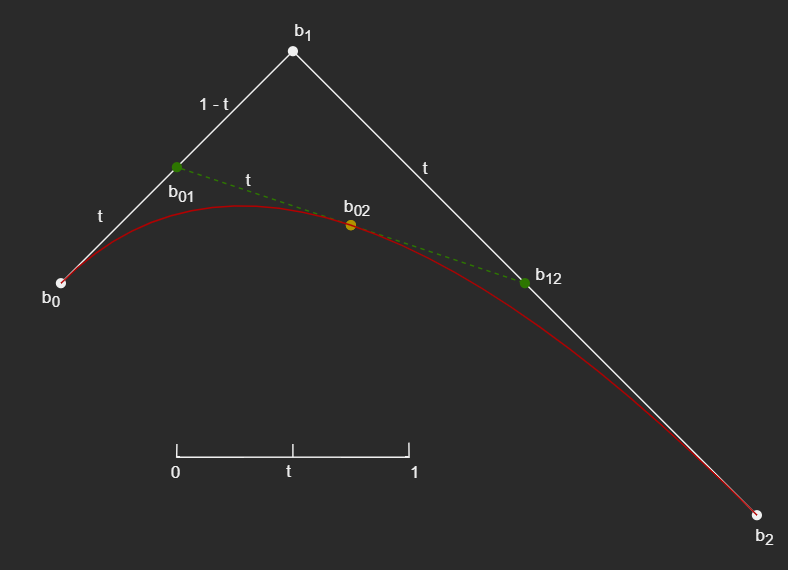
- 如上图所示，假设平面上有三个点 b0、b1、b2，时间 t 为 [0, 1]，b01 为从 b0 开始向 b1 移动，经过时间 t 后的位置，b02 同理。同时，在 t 时刻的产生的新的点 b01、b12，也找到了经过时间 t 后的位置 b02。此时，点 b02 即为这三个控制点在 t 时刻的目标点。通过在区间内的每一个时刻，找到所有对应的目标点，最终这些目标点形成的曲线，即为（二阶）贝塞尔曲线。
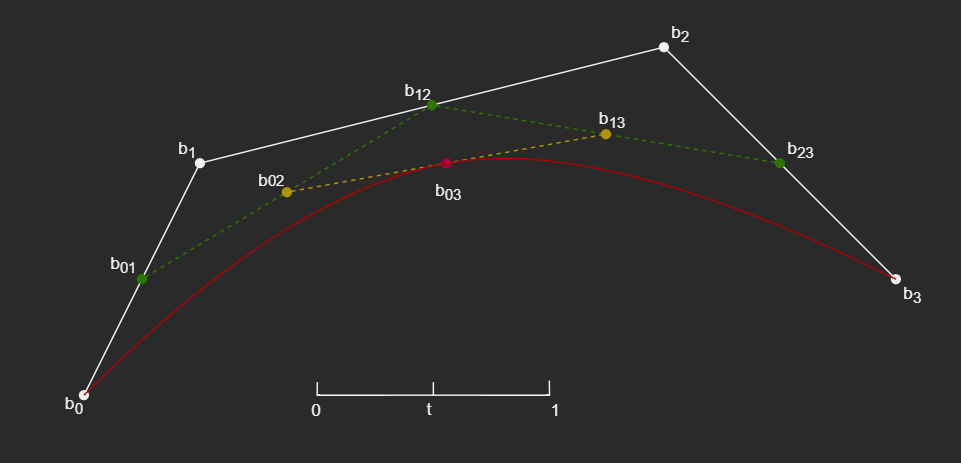
-同样，当平面上有四个控制点时，和前面一样，依次找到每条线段上 t 时刻的点，新的点组成新的线段，继续寻找 t 时刻的点，直到找到最后一个点，即为贝塞尔曲线上的点。通过将所有时间的对应点都找到，同样就能获得一条贝塞尔曲线。
代数表示
- 从二阶贝塞尔曲线图中可以看到，点 b01 为点 b0 和点 b1 的线性插值，那么点 b01 可表示为
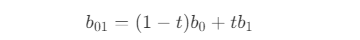
- 同样，点 b12 和点 b02 即为
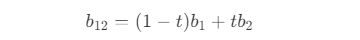
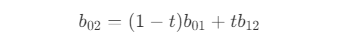
- 因此，可以得到点 b02 为
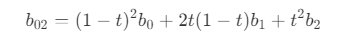
- 同理，当阶数为 n （控制点数量为 n - 1）时，则有
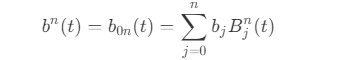其中，B 为 Bernstein Polynomials（伯恩斯坦多项式）
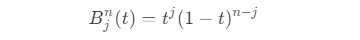
- 可以得到，n 阶贝塞尔曲线的表示为
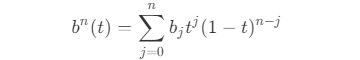
性质
- 贝塞尔曲线一定经过起点和终点
- 在三阶贝塞尔中，曲线从 b0 到 b1 的起始切线方向为 3(b1 - b0)，从 b2 到 b3 的结束切线方向为 3(b3 - b2)
- 贝塞尔曲线经过仿射变换后保持不变（投影时则不支持）
- 贝塞尔曲线一定在所有控制点形成的凸包内
分段贝塞尔曲线
- 当控制点数量较多的时候，用一条贝塞尔曲线表示，往往不能表现出控制点的真实转变，此时需要使用分段贝塞尔曲线，即使用多个三阶贝塞尔曲线进行组合，来得到最终的曲线。
- 然而，两段三阶贝塞尔曲线拼接处，可能会产生突变，为了保证连接处光滑，需要保证连接处一阶连续，即 a2、a3 和 b0、b1 （a3 即为 b0）要在同一条直线上，并且 a2 到 a3 的距离要和 b0 到 b1 的距离相等。当满足一阶连续时，则能得到光滑的曲线。
贝塞尔曲面
- 对一个平面，取多组水平方向的控制点，分别得到水平方向多条贝塞尔曲线，再从这些曲线中取控制点，绘制竖直方向的贝塞尔曲线，最终这些曲线即形成一个贝塞尔曲面。
总结
- 贝塞尔曲线是计算机图形中应用较多的曲线，通过分段贝塞尔曲线，能满足大部分曲线的绘制需求。另外，还有其他曲线，如 Spline（样条）、B-Splines（B样条）等，也是计算机图形中使用的曲线。