在几何中,重心坐标有特别的性质,相应也有许多用途,其中重心坐标插值在图形学中也有广泛应用。
简介
- 设 三角形ABC 的顶点坐标为 v,对于ABC 中的任意一点 P ,如果存在 α 、 β 、γ ,使得
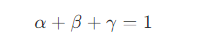
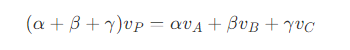 那么点 (α, β, γ) 即为点 P 在 三角形ABC 中的(归一化)重心坐标。此时由三个顶点和 P 点划分的三个三角形的面积比例为 α:β:γ 。
那么点 (α, β, γ) 即为点 P 在 三角形ABC 中的(归一化)重心坐标。此时由三个顶点和 P 点划分的三个三角形的面积比例为 α:β:γ 。
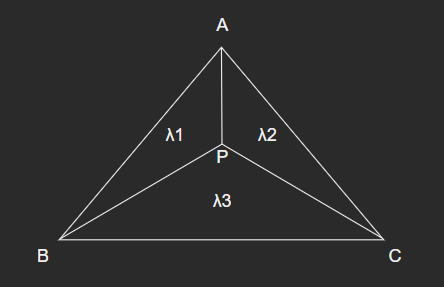
- 可以看出,对于三角形中任意一个点,通过找到其重心坐标,即找到该点相对于三个顶点的权重,就可以通过三个顶点的数据,对该点进行插值,从而对三角形中的所有点都可以进行插值,这种插值方式即为重心坐标插值。
- 因此,重心坐标插值的核心,即找到每个点对应的权重 α 、 β 、 γ 。
重心坐标推导
- 三角形PAB 的面积为
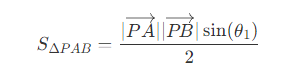 其中
其中
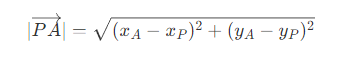
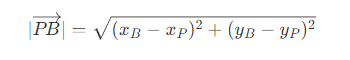
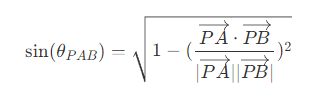 推导得到
推导得到
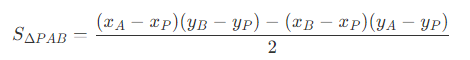 因此,同理可以得到
因此,同理可以得到
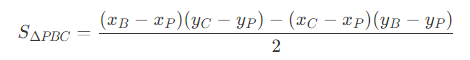
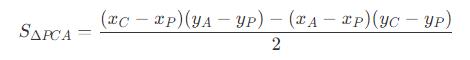
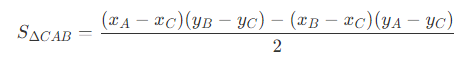
- 知道了每个三角形的面积后,每个顶点对应的权重为
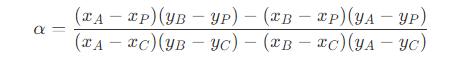
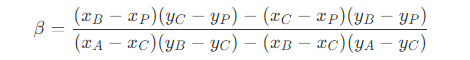
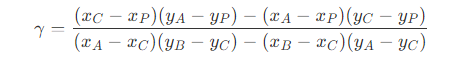
- 此时点 P 可以表示为
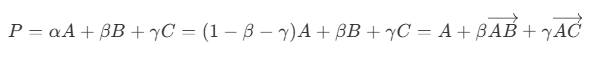
向量点乘方案
- 向量叉乘计算是通过面积比例来计算的,重心坐标还能通过向量点乘的方式来进行。向量 AP 可以表示为
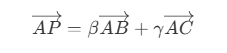
- 两边分别乘上向量 AB 和 AC ,可以得到
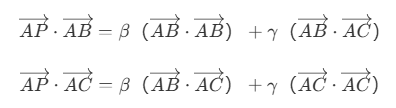 解方程组可以得到
解方程组可以得到
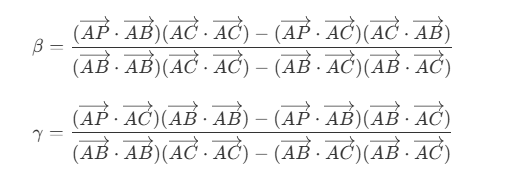
透视校正插值
- 渲染流水线中,重心坐标插值,通常是在光栅化阶段,对屏幕空间(Screen Space)下的像素进行,而不是在观察空间(View Space)下进行。由于透视投影不是线性变换,因此变换后的三角形和变换前的形状可能会发生变化,如下图所示
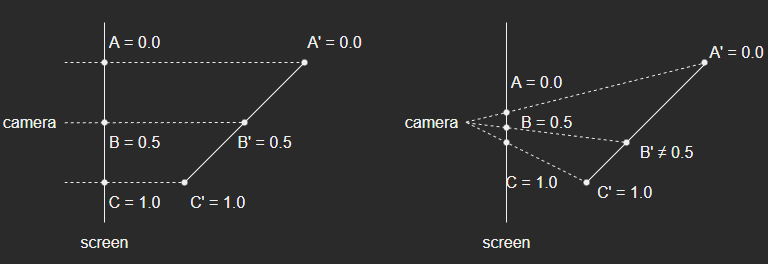
正交投影(左)和 透视投影(右)的示例 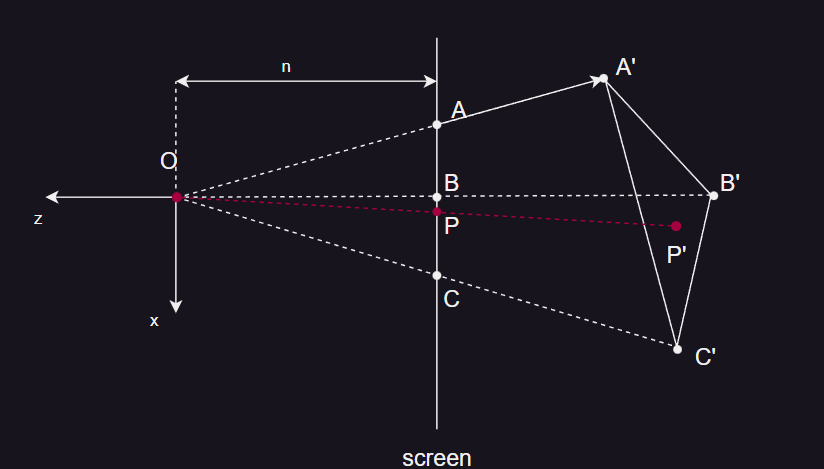
2D 推导
- 以 A’B' 为例,其直线方程为
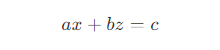
- 以点 A 和 A' 为例,由相似三角形关系可以得到
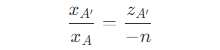
- 则有
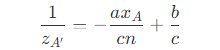
- 因此,对 A’B' 上的任意一点都有
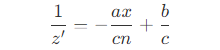
- 假设点 P 为 AB 上的一点,其中
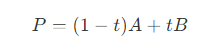
- 可以得到对应 A’B' 上的点 P' 为
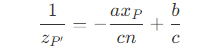
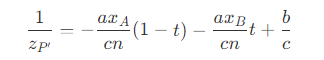
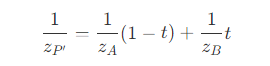
- 也就是说,对于屏幕空间下的直线上的点的深度插值,为观察空间下的深度倒数的插值。
3D 推导
- 三角形 A’B’C' 所在的平面方程为
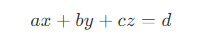
- 类比 2D 推导,可以得到
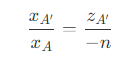
- 同样,对于 yoz 平面,也有
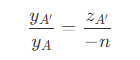
- 因此,可以得到
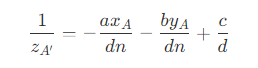
- 也就是说,对于三角形 A’B’C' 中的一点,有
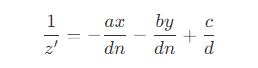
- 假设 P 为 三角形 ABC 的重心,则有
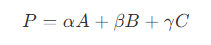
- 其中
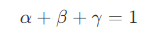
- 那么,对应三角形 A’B’C' 上的点 P' ,有
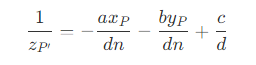
- 其中
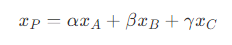
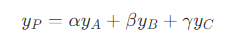
- 整理可得
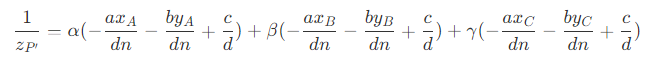
- 因此可以得到
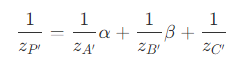
- 也就是说,对于屏幕空间下的平面上的点的深度插值,为观察空间下的深度倒数的插值。
总结
- 重心坐标插值方法,在图形学中应用相对比较广泛,深度、法线、颜色等都可以通过这种方式进行插值。了解重心坐标的概念和推导方式后,还需要注意透视投影带来的问题,需要通过校正后,才能得到正确的插值表现。