环境光遮蔽（AO）技术，用于模拟场景中的光照，使场景中的物体看起来更加真实。

简介

• 随着设备的更新换代，现代游戏玩家对画面质量的要求越来越高，全局光照成为提升游戏视觉效果的关键技术。全局光照技术基于物理光学原理，通过计算光线在场景中的反射、折射和散射等过程，模拟真实世界的光照效果，使得游戏场景看起来更加逼真。然而，这种真实带来的代价就是计算成本过高，离线生成一个静态场景的效果可能需要花上几个小时，并不适用于实时渲染。因此，需要通过简单但在视觉上仍然令人信服的解决方案的进行替代，一种基本的全局照明效果是环境光遮蔽（Ambient Occlusion）。

基础概念

立体角（Solid Angle）

• 平面角定义为角所对的弧长 s 与半径 r 的比值，用 ω 表示。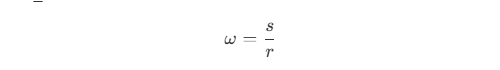
• 立体角（Solid Angle）则是在三维空间下的角度，其所对的面积 A 与半径 r 的平方的比值，用 Ω 表示。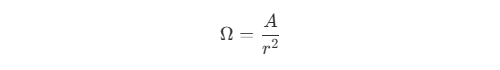
• 立体角通过 θ 和 φ 两个角度来表示，其中 θ 是与 z 轴的夹角，φ 是与 x 轴或 y 轴的夹角。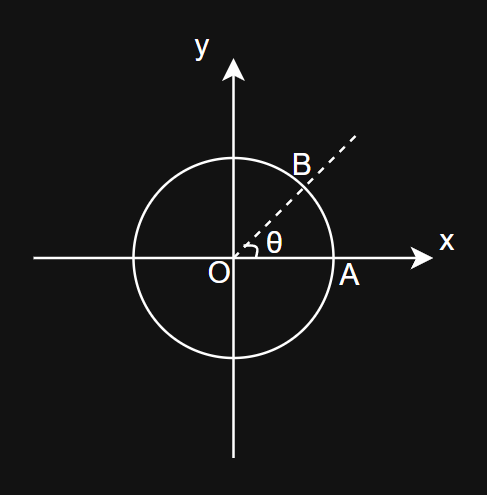
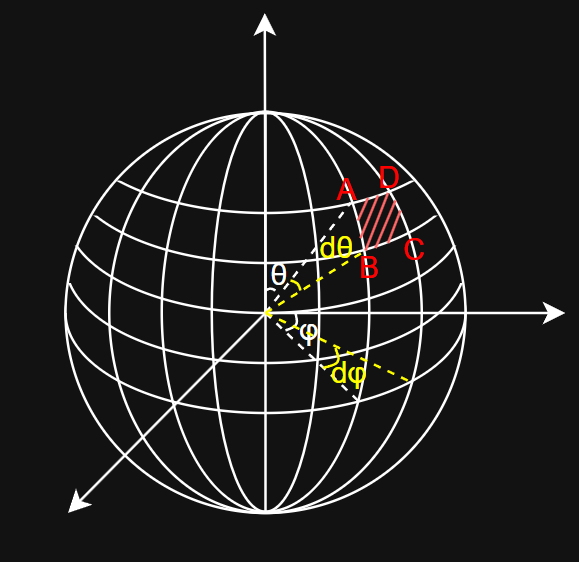
• 如图所示，对于单位立体角 dΩ（即 dθ 和 dφ），其所对的面积 A 即为矩形 ABCD（近似）的面积，即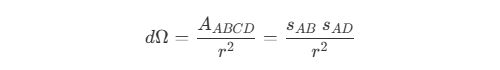 其中，AB 为 dθ 对应的弧长，CD 为 dφ 对应的弧长，则有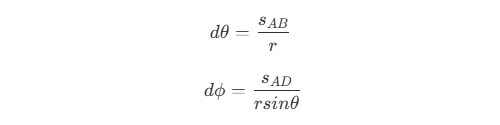 因此

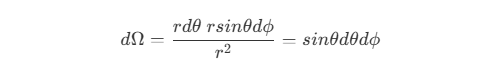
辐射能量（Radiant Energy）

• 辐射能量（Radiant Energy）是指电磁辐射的能量，用 Q 表示。

辐射通量（Radiant Flux）

• 辐射通量（Radiant Flux）是指单位时间内的辐射能量，用 Φ 表示。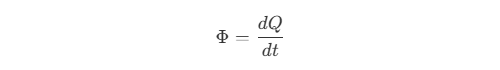 其中，Q 是辐射能量，t 是时间。

辐射强度（Radiant Intensity）

• 辐射强度（Intensity）是指单位立体角内的辐射通量（所有面积光总和），用 I 表示。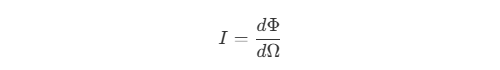 其中，Φ 是总辐射通量，Ω 是立体角。

辐照度（Irradiance）

• 辐照度（Irradiance）是指单位面积上接收到的辐射通量（所有立体角方向总和），用 E 表示。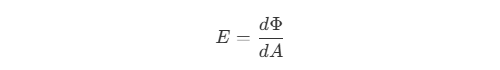 其中，Φ 是总辐射通量，A 是接收面积。

辐射率（Radiance）

• 辐射率（Radiance）是指单位立体角，在单位面积上辐射通量，用 L 表示。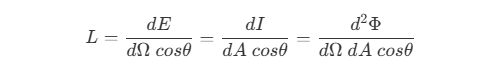 其中，Φ 是总辐射通量，Ω 是立体角，A 是接收或光源面积，对应入射或出射辐射率。基于理想漫反射表面（Lambert 表面），只有垂直于光的投影面积，才是真正的辐射面积，所以辐射率最终需要对面积进行修正，即 A cosθ。
• 由于总辐射通量是所有面积所有方向的辐射通量总和，所以需要对立体角和面积进行二次微分。

渲染方程（Rendering Equation）

• 渲染方程（Rendering Equation）是全局光照模型中的基本方程，用于描述光在场景中的传播和反射。渲染方程的基本形式为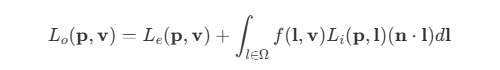： 其中，p 为观察的物体表面位置，v 为观察方向，l 为光的入射方向，n 为物体表面法线，n · l 表示入射光被物体表面接收（和投影面垂直）的比例，f 为物体表面反射率（接收到的光反射到观察方向的比例）。

环境光遮蔽（Ambient Occlusion）

• 为了实现全局光照模型效果，则需要求解渲染方程，常用的方法有两种，即有限元方法和蒙特卡洛方法。其中，光能传递是基于有限元方法的算法，各种形式的光线追踪则是使用蒙特卡洛方法。然而，这些方法虽然可以产生较好的效果，但生成一帧图像可能需要花费数个小时，并不适用与动态场景。
• 为了将全局光照效果应用到计算生成的场景中，需要使用一些简化的模型方法，一种基本的方法是环境光遮蔽（Ambient Occlusion，AO）。为了简化，假设两个条件：
  • 物体表面为 Lambert 表面。
  • 入射辐射率在各个方向上都为相同的常量 L' 。
• 根据前面的辐射率公式，可以得到辐照度 E 为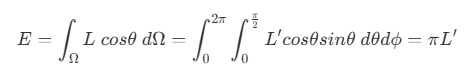
• 然而，当前辐照度并未考虑可见性，即某些方向的光可能被场景中其他物体或自身某些部分阻挡，则这些方向的入射辐射度不为 L'。假设来自被遮挡方向的入射辐射度为 0 ，未被遮挡方向的入射辐射度为 1，则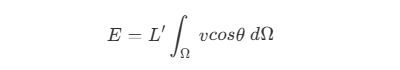 其中，v 为可见性函数，L' 后的积分部分为环境光遮蔽因子，用 k 表示，即
• 当所有方向都没有遮挡时，v 为 1 ，此时 k 有最大值。当所有方向都被遮挡时，v 为 0 ，此时 k 有最小值。
• 因此，归一化的环境光遮蔽因子 k' 为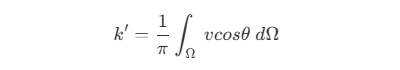 辐照度 E 为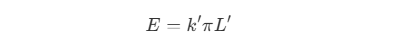
• 通过环境光遮蔽方法计算全局光照效果，最终会转换为通过计算环境遮挡因子实现。计算环境遮挡因子可能很耗时，通常需要执行在渲染之前离线进行。预先计算任何与光照相关的过程，包括环境遮挡在内的信息，通常被称为烘焙。预计算环境光遮挡最常见的方法是通过蒙特卡洛方法，即在法线周围的半球面上，均匀地随机取 N 个方向，并沿着这些方向追踪光线，检查这些方向最终是否可见，对结果求平均值，即为 k' 的估算值，则能计算出对应的辐照度。

屏幕空间环境光遮蔽（Screen Space Ambient Occlusion）

• 计算环境遮挡因子的离线方法，能得到较好的表现效果，但需要进行光线追踪计算，计算成本较高，且仅适用于静态场景。对于实时动态场景，需要使用更加简化的模型，避免大部分此类计算。对于动态场景，可以通过将物体进行分组后，再用简化模型替代每一组，之后计算每一个简化模型的 SDF 信息，就能通过锥体追踪得到光线的遮挡信息。
• 然而，在物体空间下进行计算的方法，随着场景复杂度的提升，计算量会越来越大，造成新的性能压力。事实上，关于遮挡的一些信息可以完全从屏幕空间数据中推断出来，如：深度、法线，这些数据在渲染过程中已经生成。屏幕空间下计算的方法，不受场景复杂度的影响，而是仅和渲染过程使用的分辨率相关，因此具有恒定的计算成本。
• 屏幕空间下的环境光遮蔽（Screen Space Ambient Occlusion，SSAO），通过使用 z-buffer 深度缓冲区作为唯一输入，来估算每个像素的环境遮挡因子。在以像素位置为圆心的球面上，随机取一组采样点，进行深度测试，最终通过深度测试的样本数量占比即为环境遮挡因子。
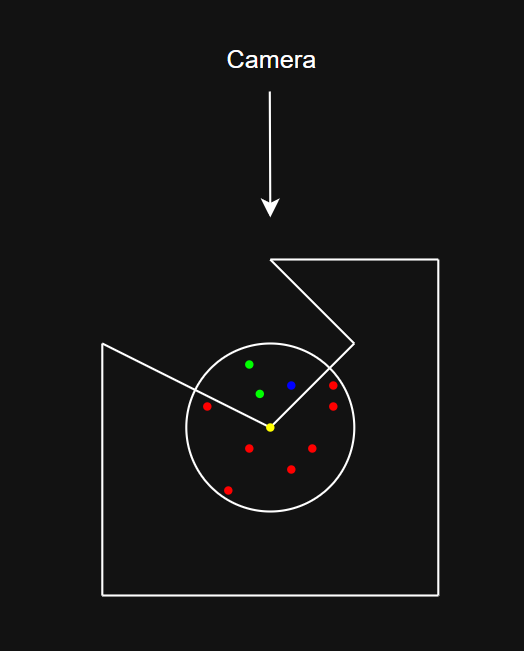
• 如图所示，相机在正上方，黄色点为当前计算的像素位置点，其余点为采样点，分布在以黄色点为圆心的球面上。其中，红色点在物体内部，即未通过深度测试，而蓝色点虽然在物体外部，但在相机方向上被遮挡，即同样未通过深度测试，仅绿色点能通过深度测试，因此环境遮挡因子 k' 为 0.2 。
• 其中，样本的选取，不是只考虑位于表面上方半球内的位置，而是包括了物体内部的位置。在这种采样方式下，会出现一个平坦的表面会变暗，且边缘比周围更亮的情况。尽管如此，这种表现结果通常在视觉上依然能令人满意。

Unity 中的 SSAO 实现

• URP（14.0.12）中的 SSAO 实现在 ScreenSpaceAmbientOcclusion.cs 中，主要代码如下：

// ./Runtime/RenderFeatures/ScreenSpaceAmbientOcclusion.cs

...

            public override void Execute(ScriptableRenderContext context, ref RenderingData renderingData)
            {
                if (m_Material == null)
                {
                    Debug.LogErrorFormat("{0}.Execute(): Missing material. ScreenSpaceAmbientOcclusion pass will not execute. Check for missing reference in the renderer resources.", GetType().Name);
                    return;
                }

                var cmd = renderingData.commandBuffer;
                using (new ProfilingScope(cmd, m_ProfilingSampler))
                {
                    ...

                    GetPassOrder(m_BlurType, m_CurrentSettings.AfterOpaque, out int[] textureIndices, out ShaderPasses[] shaderPasses);

                    // Execute the SSAO
                    RTHandle cameraDepthTargetHandle = m_Renderer.cameraDepthTargetHandle;
                    RenderAndSetBaseMap(ref cmd, ref renderingData, ref m_Renderer, ref m_Material, ref cameraDepthTargetHandle, ref m_SSAOTextures[0], ShaderPasses.AmbientOcclusion);

                    // Execute the Blur Passes
                    for (int i = 0; i < shaderPasses.Length; i++)
                    {
                        int baseMapIndex = textureIndices[i];
                        int targetIndex = textureIndices[i + 1];
                        RenderAndSetBaseMap(ref cmd, ref renderingData, ref m_Renderer, ref m_Material, ref m_SSAOTextures[baseMapIndex], ref m_SSAOTextures[targetIndex], shaderPasses[i]);
                    }

                    // Set the global SSAO Params
                    cmd.SetGlobalVector(s_AmbientOcclusionParamID, new Vector4(1f, 0f, 0f, m_CurrentSettings.DirectLightingStrength));
                }
            }

...

• SSAO 执行过程主要包括几个步骤：
  • 通过 GetPassOrder 方法，获得当前模糊类型对应需要执行的 Pass 组。
  • 通过 RenderAndSetBaseMap 方法，传入深度图，执行 ScreenSpaceAmbientOcclusion.shader 的 Pass 0（ShaderPasses.AmbientOcclusion），输出到 m_SSAOTextures[0] 上。
  • 遍历 Pass 组，通过 RenderAndSetBaseMap 方法，将上一次的输出结果作为输入，执行每一个 Pass 输出。
  • 设置 s_AmbientOcclusionParamID 。

SSAO Pass

• ShaderPasses.AmbientOcclusion 对应的 Pass 的像素着色器为 SSAO ，其实现如下：

// ./ShaderLibrary/SSAO.hlsl

...

half4 SSAO(Varyings input) : SV_Target
{
    UNITY_SETUP_STEREO_EYE_INDEX_POST_VERTEX(input);
    float2 uv = input.texcoord;
    // Early Out for Sky...
    float rawDepth_o = SampleDepth(uv);
    // 1. 过滤深度范围，去除过小（天空盒距离）/过大（用户设置距离）
    if (rawDepth_o < SKY_DEPTH_VALUE)
        return PackAONormal(HALF_ZERO, HALF_ZERO);

    // Early Out for Falloff
    float linearDepth_o = GetLinearEyeDepth(rawDepth_o);
    half halfLinearDepth_o = half(linearDepth_o);
    if (halfLinearDepth_o > FALLOFF)
        return PackAONormal(HALF_ZERO, HALF_ZERO);

    float2 pixelDensity;
    #if defined(SUPPORTS_FOVEATED_RENDERING_NON_UNIFORM_RASTER)
    UNITY_BRANCH if (_FOVEATED_RENDERING_NON_UNIFORM_RASTER)
    {
        pixelDensity = RemapFoveatedRenderingDensity(RemapFoveatedRenderingNonUniformToLinear(uv));
    }
    else
    #endif
    {
        pixelDensity = float2(1.0f, 1.0f);
    }

    // 2. 计算当前像素的法线、世界坐标（以相机为原点）
    // Normal for this fragment
    half3 normal_o = SampleNormal(uv, linearDepth_o, pixelDensity);

    // View position for this fragment
    float3 vpos_o = ReconstructViewPos(uv, linearDepth_o);

    // Parameters used in coordinate conversion
    // 传入的 VP 矩阵在 ScreenSpaceAbmibentOcclusion.OnCameraSetup 中特殊处理了，移除了相机的位移变换，即假设相机为世界坐标原点
    half3 camTransform000102 = half3(_CameraViewProjections[unity_eyeIndex]._m00, _CameraViewProjections[unity_eyeIndex]._m01, _CameraViewProjections[unity_eyeIndex]._m02);
    half3 camTransform101112 = half3(_CameraViewProjections[unity_eyeIndex]._m10, _CameraViewProjections[unity_eyeIndex]._m11, _CameraViewProjections[unity_eyeIndex]._m12);

    const half rcpSampleCount = half(rcp(SAMPLE_COUNT));
    half ao = HALF_ZERO;
    half sHalf = HALF_MINUS_ONE;
    UNITY_UNROLL

    // 3. 采样多个点，计算 ao 值
    for (int s = 0; s < SAMPLE_COUNT; s++)
    {
        sHalf += HALF_ONE;

        // 3.1 取采样点，计算其世界坐标（以相机为原点）和屏幕坐标
        // Sample point
        half3 v_s1 = PickSamplePoint(uv, s, sHalf, rcpSampleCount, normal_o, pixelDensity);
        half3 vpos_s1 = half3(vpos_o + v_s1);
        half2 spos_s1 = half2(
            camTransform000102.x * vpos_s1.x + camTransform000102.y * vpos_s1.y + camTransform000102.z * vpos_s1.z,
            camTransform101112.x * vpos_s1.x + camTransform101112.y * vpos_s1.y + camTransform101112.z * vpos_s1.z
        );

        // 3.2 计算采样点深度值和uv
        half zDist = HALF_ZERO;
        #if defined(_ORTHOGRAPHIC)
            zDist = halfLinearDepth_o;
            half2 uv_s1_01 = saturate((spos_s1 + HALF_ONE) * HALF_HALF);
        #else
            // 从世界空间变换到观察空间，并取反，得到深度值
            zDist = half(-dot(UNITY_MATRIX_V[2].xyz, vpos_s1));
            half2 uv_s1_01 = saturate(half2(spos_s1 * rcp(zDist) + HALF_ONE) * HALF_HALF);
        #endif

        #if defined(SUPPORTS_FOVEATED_RENDERING_NON_UNIFORM_RASTER)
        UNITY_BRANCH if (_FOVEATED_RENDERING_NON_UNIFORM_RASTER)
        {
            uv_s1_01 = RemapFoveatedRenderingLinearToNonUniform(uv_s1_01);
        }
        #endif

        // 3.3 计算采样点对应的uv，在深度图中的深度值，并检查采样点深度是否该深度的半径范围内
        // Relative depth of the sample point
        float rawDepth_s = SampleDepth(uv_s1_01);
        float linearDepth_s = GetLinearEyeDepth(rawDepth_s);

        // We need to make sure we not use the AO value if the sample point it's outside the radius or if it's the sky...
        half halfLinearDepth_s = half(linearDepth_s);
        half isInsideRadius = abs(zDist - halfLinearDepth_s) < RADIUS ? 1.0 : 0.0;
        isInsideRadius *= rawDepth_s > SKY_DEPTH_VALUE ? 1.0 : 0.0;

        // 3.4 计算深度图该深度值对应的点和当前像素点的相对坐标
        // Relative postition of the sample point
        half3 v_s2 = half3(ReconstructViewPos(uv_s1_01, linearDepth_s) - vpos_o);

        // 3.5 计算每个采样点的 ao 影响
        // Estimate the obscurance value
        // kBeta 为防止自遮蔽的偏置量
        half dotVal = dot(v_s2, normal_o) - kBeta * halfLinearDepth_o;
        // 采样点的向量在法线上的投影，正半球会产生遮蔽
        half a1 = max(dotVal, HALF_ZERO);
        // 距离越近，遮蔽贡献更大，kEpsilon 防止出现分母为 0
        half a2 = dot(v_s2, v_s2) + kEpsilon;
        ao += a1 * rcp(a2) * isInsideRadius;
    }

    // 4. 计算最终的 ao 值
    // Intensity normalization
    // a1 为 O(RADIUS) ，a2 为 O(RADIUS^2)，ao = a1 / a2 导致 ao 受 RADIUS 影响，乘上 RADIUS 抵消该影响。
    ao *= RADIUS;

    // Calculate falloff...
    half falloff = HALF_ONE - halfLinearDepth_o * half(rcp(FALLOFF));
    falloff = falloff*falloff;

    // Apply contrast + intensity + falloff^2
    ao = PositivePow(saturate(ao * INTENSITY * falloff * rcpSampleCount), kContrast);

    // 5. 将 ao 和法线打包返回，a 为 ao，gba 为法线
    // Return the packed ao + normals
    return PackAONormal(ao, normal_o);
}

...

• SSAO Pass 主要通过取多个采样点，计算深度符合要求的且在当前点正半球上的点的 ao 值，累加后求平均值，得到所有采样点在当前点上产生的最终 ao 值。

Blur Pass

• SSAO Pass 计算完成后，还需要根据不同的设置进行双边滤波，主要如下：

模糊类型	渲染顺序	Pass组
Bilateral	不透明渲染前	BilateralBlurHorizontal（1） BilateralBlurVertical（2） BilateralBlurFinal（3）
Bilateral	不透明渲染后	BilateralBlurHorizontal（1） BilateralBlurVertical（2） BilateralAfterOpaque（3）
Gaussian	不透明渲染前	GaussianBlurHorizontal（5） GaussianBlurVertical（6）
Gaussian	不透明渲染后	GaussianBlurHorizontal（5） GaussianAfterOpaque（7）
Kawase	不透明渲染前	KawaseBlur（8）
Kawase	不透明渲染后	KawaseAfterOpaque（9）

• 模糊的核心方法为 Blur 和 BlurSmall ，其中 Blur 取水平或竖直的点进行模糊计算，而 BlurSmall 取对角线进行计算。Blur 的实现如下：

// ./ShaderLibrary/SSAO.hlsl

...

half4 Blur(const float2 uv, const float2 delta) : SV_Target
{
    half4 p0 =  SAMPLE_BASEMAP(uv                       );
    half4 p1a = SAMPLE_BASEMAP(uv - delta * 1.3846153846);
    half4 p1b = SAMPLE_BASEMAP(uv + delta * 1.3846153846);
    half4 p2a = SAMPLE_BASEMAP(uv - delta * 3.2307692308);
    half4 p2b = SAMPLE_BASEMAP(uv + delta * 3.2307692308);

    half3 n0 = GetPackedNormal(p0);

    half w0  =                                           half(0.2270270270);
    // CompareNormal 用于过滤掉和当前点法线偏差过大的采样点
    half w1a = CompareNormal(n0, GetPackedNormal(p1a)) * half(0.3162162162);
    half w1b = CompareNormal(n0, GetPackedNormal(p1b)) * half(0.3162162162);
    half w2a = CompareNormal(n0, GetPackedNormal(p2a)) * half(0.0702702703);
    half w2b = CompareNormal(n0, GetPackedNormal(p2b)) * half(0.0702702703);

    half s = half(0.0);
    s += GetPackedAO(p0)  * w0;
    s += GetPackedAO(p1a) * w1a;
    s += GetPackedAO(p1b) * w1b;
    s += GetPackedAO(p2a) * w2a;
    s += GetPackedAO(p2b) * w2b;
    s *= rcp(w0 + w1a + w1b + w2a + w2b);

    return PackAONormal(s, n0);
}

...

• 最后一步的模糊处理和前面的稍有不同，以 Bilateral 为例，最后一个模糊处理的像素着色器 FinalBlur 的实现如下：

// ./ShaderLibrary/SSAO.hlsl

...

half4 FinalBlur(Varyings input) : SV_Target
{
    UNITY_SETUP_STEREO_EYE_INDEX_POST_VERTEX(input);

    const float2 uv = input.texcoord;
    const float2 delta = _SourceSize.zw * rcp(DOWNSAMPLE);
    return HALF_ONE - BlurSmall(uv, delta );
}

...

• 在最后一个模糊处理完成前，ao 值代表遮蔽量，而最后一个模糊处理完成后的值，会设置到 directAmbientOcclusion 和 indirectAmbientOcclusion 上，在计算光照的时候进行相乘，所以需要的是光照可达性，即 1 - ao。
• 而对于在不透明渲染完成后的 ao 计算，则还需要进行其他处理，同样以 Bilateral 为例，最后一个模糊处理的 Pass 的实现如下：

// ./Shader/Utils/ScreenSpaceAmbientOcclusion.shader

...

        Pass
        {
            Name "SSAO_Bilateral_FinalBlur_AfterOpaque"

            ZTest NotEqual
            ZWrite Off
            Cull Off
            Blend One SrcAlpha, Zero One
            BlendOp Add, Add

            HLSLPROGRAM
                #pragma vertex Vert
                #pragma fragment FragBilateralAfterOpaque

                #include_with_pragmas "Packages/com.unity.render-pipelines.core/ShaderLibrary/FoveatedRenderingKeywords.hlsl"
                #include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/SSAO.hlsl"

                half4 FragBilateralAfterOpaque(Varyings input) : SV_Target
                {
                    half ao = FinalBlur(input).r;
                    return half4(0.0, 0.0, 0.0, ao);
                }

            ENDHLSL
        }

...

• 在不透明渲染后的最后模糊处理，直接将 1 - ao 作为 a 通道输出。可以看到，此 Pass 采用了 Blend One SrcAlpha, Zero One，即

通道	Src因子	Dst因子	公式	输出结果 （像素着色器的返回是(0, 0, 0, ao)）
RGB	One	SrcAlpha	SrcColor * One + DstColor * SrcAlpha	缓冲区颜色 * ao
A	Zero	One	SrcAlpha * Zero + DstAlpha * One	缓冲区透明度

• 不透明渲染后的 SSAO，最终利用 ao 值直接和缓冲区的结果进行混合，不需要额外写一个读取场景颜色再乘回去的全屏 Pass，也不需要进行现有 Shader 的改造，就能获得 AO 效果，实现简单。但在物理上是错误的，因为 AO 同时遮蔽了直射光和高光，画面会比正常更暗。
• 尽管如此，此方案也因为其兼容性和便利性，而被一些项目采用，甚至在观感上认为此表现的对比度更强，更符合美术期望。

总结

• 环境光遮蔽在当代游戏项目中的使用越来越普遍，尽管其实现并不算复杂，但其覆盖的概念较多。从基础概念起进行理解推导，更容易掌握其实现过程。此外，Unity 中的 SSAO 实现在细节上有其特别的思路和算法，了解其实现有助于在 SSAO 的使用上找到合适的性能优化方案。

参考

• Real-Time Rendering 4th Edition

---

• Next Post →