八叉树是基于空间划分的结构,在很多场景下能达到加速计算的效果。
简介
- 八叉树和轴对齐 BSP 树相似,沿长方体的三个轴同时进行分割,分割点经过长方体的中心,得到均等的 8 个新的长方体子节点,子节点继续分割,直到达到设定的最大层级,或者单个节点的物体数量少于设定的数量,从而将空间结构划分成树结构。四叉树是八叉树的 2D 版本,即沿平面的两个轴进行分割,如下图所示:
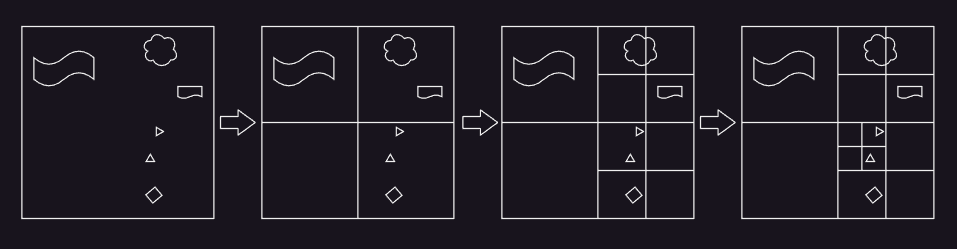
八叉树结构
- 八叉树的节点主要包括:
- 物体列表:当前节点所包含的物体。
- 包围盒:当前节点的 AABB 包围盒。
- 子节点列表:当前节点细分后的子节点。
- 树的主要方法为:
- 插入。
- 查询。
插入
- 从根节点开始,检查当前节点是否有子节点。
- 如果当前节点有子节点,则根据新的物体的坐标,找到符合坐标范围的子节点,作为新的当前节点。
- 如果当前节点没有子节点,则检查当前节点下有多少物体。
- 如果当前节点的物体没有达到上限,则将新的物体加入当前节点,插入流程结束。
- 如果当前节点的物体已经达到上限,则将当前节点进行细分,创建子节点。
- 将当前节点的物体根据坐标划分到子节点中。
- 根据新的物体的坐标,找到符合坐标范围的子节点,作为新的当前节点。
- 重复上述步骤,将新的物体插入到当前节点。
查询
- 从根节点出发,检查当前节点包围盒和目标范围包围盒是否相交。
- 如果当前节点包围盒与目标包围盒不相交,则该节点及其任何子节点都没有任何物体处在目标范围内,不再往下检查。
- 如果当前节点包围盒与目标包围盒相交,则
- 如果当前节点不为叶节点时,则重复上述步骤,逐一检查子节点。
- 如果当前节点为叶节点,则检查叶节点中的物体是否在目标范围内。
松散八叉树
- 如上图所示,右上角的云朵,在第二次划分时,同时处在两个节点中。如果不进行第二次划分,则右下角的小三角形会处在较高的层级,效率比较低。如果将云朵切分成两个,就能分别放进去各自节点中,但是会产生更多的物体物体。而 Ulrich 提出了松散八叉树的方案。
- 松散八叉树的基本思想和普通八叉树一致,但每个节点的长方体大小选择比较宽松。如果普通八叉树的节点长方体的边长为 l ,则松散八叉树的为 kl ,其中 k > 1 。
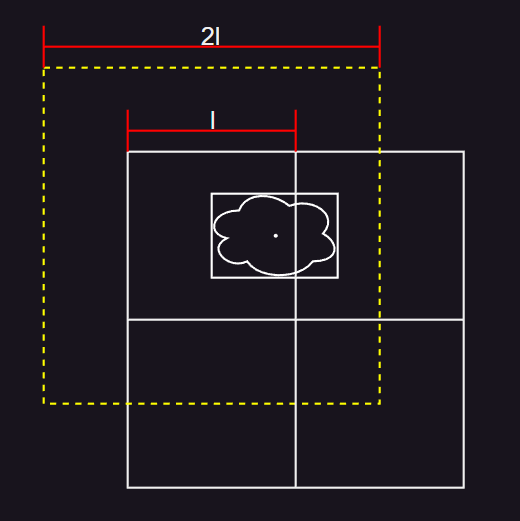
- 如上图所示,白色框为普通八叉树的范围,边长为 l ,黄色框为松散八叉树的范围,边长为 2l 。对于普通八叉树,云朵跨过了两个节点,而对于松散八叉树,云朵包围盒的中心点处在普通八叉树左上节点范围中,包围盒处在左上松散八叉树节点范围内,因此归属于左上松散八叉树节点。
- 可以看到,通过使用大的长方体,可以减少穿过分割平面的物体数量,从而将物体沿八叉树放在更深的位置,并且通常一个物体只会归属一个节点,对树进行删除操作就比较容易。
- 另外,物体通常会进行移动,比起普通八叉树,在松散八叉树下,由于节点的范围变大了,因此物体小范围的移动超出节点的概率变小了,从而减少了节点更新的频率。
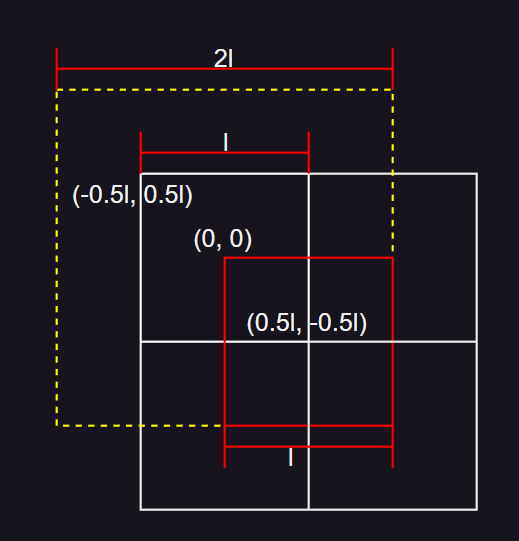
- 假设普通八叉树节点的长方体边长为 l,则此节点中的物体,包围盒边长 ≤ l 。
- 为了保证处在对应松散八叉树节点中,物体的中心点最远只能移动到普通八叉树节点长方体边界上。
- 假设节点的中心点坐标为 (0, 0) ,此时松散八叉树每个轴的范围为 (-l, l) ,即此时 k = 2 。
- 由于物体大小已知,所以物体包围盒的中心点坐标和边长都可以得到,则可以直接计算得到物体能插入的最深的节点位置。步骤为:
- 计算物体的包围盒,得到中心点坐标和包围盒边长。
- 根据包围盒边长,在设置的最大层级内,计算得到该物体的最深层级。
- 在最深层级上,根据物体的中心点坐标,计算对应的节点位置,将物体插入(删除)。
- 因此,对松散八叉树来说,当 k = 2 时,对已知大小的物体,插入和删除操作可以在 O(1) 时间内完成。
- 然而,由于松散八叉树的范围较大,所以查找的时候,对于同一个范围,比起普通八叉树,松散八叉树需要遍历更多的的节点。另外,由于节点间的范围有重合,因此一定程度上会失去较好的分类顺序。尽管如此,在多数情况下,松散八叉树还是会降低碰撞检测过程中组合测试的计算量。
应用
碰撞检测
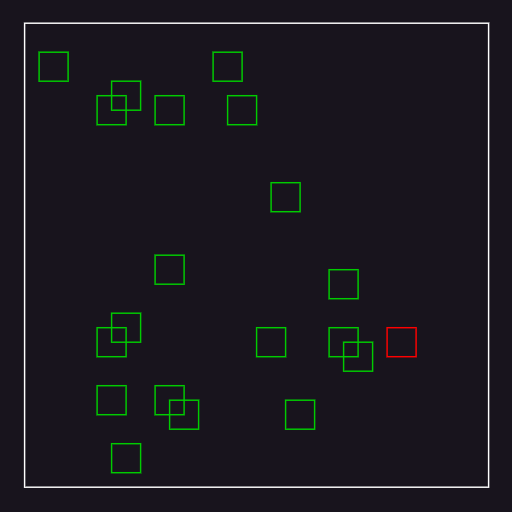
- 对场景中的物体做碰撞检测时,如上图的红色物体,图中总共有 20 个物体,则需要进行 20 次比对。随着物体的增多,检测的效率会非常低。
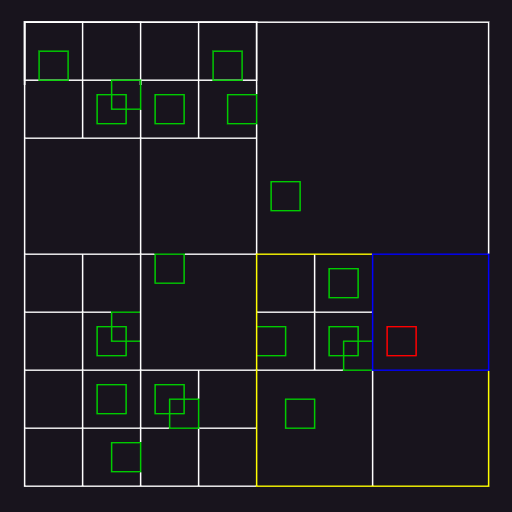
- 将场景划分成八叉树(图中为 2D 表示),可以看到,当要对红色物体做碰撞检测时,从根节点出发,找到红色物体所处的黄色框节点,再从黄色框中找到蓝色框节点,发现其中只有一个物体,因此红色物体只需要进行 2 次查找即完成碰撞检测,效率大大提高。
- 如果物体大小不一,且出现在边界上时,可以构建松散八叉树。多数情况下,松散八叉树同样可以降低碰撞过程中组合测试的计算量。
颜色量化
- 现代计算机中的图像,通常都用 RGB24 表示,即每个像素有 24 bit ,对于一张 1024 x 768 的图片,大小为 2.25 MB 。在一些内存空间相对小的环境中,如移动设备上,是一个较大的内存开销,因此人们发明了调色板,即用一个表格存放图像中的所有颜色,而实际图像数据不再是 RGB 数据,而是 RGB 数据在那个表格中的索引。对一个 RGB24 ,就有 256 x 256 x 256 = 16777216 种颜色,当使用调色板时,就能使用较少的颜色数表现出较好的近似效果,从而能在较低档次的设备上展示。
- 八叉树量化法,是常用的量化方法之一。对于一个 RGB24 颜色,则 RGB 分量各有 8 位。而八叉树的每一层,即为将每个颜色分量的每一位的组合,从根节点到叶节点就得到一种颜色,叶节点的数量即代表颜色的数量,每个叶节点的像素数量即代表当前图像有多少像素使用这个颜色。
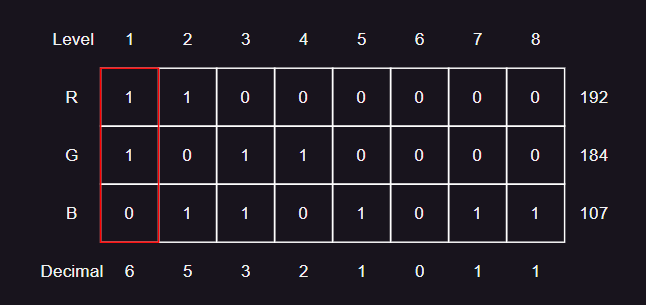
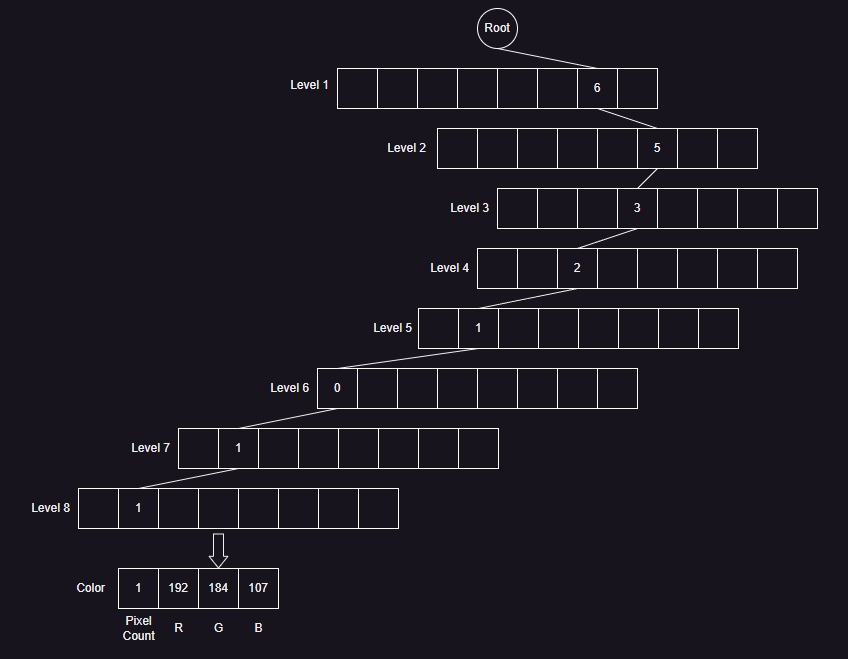
- 量化的步骤为:
- 读取图像的每个像素,如果叶节点的数量不大于设定的颜色数量上限 n ,根据颜色沿着八叉树向下查找,则将颜色插入到八叉树中。
- 如果最底层的节点不为叶节点,则创建新的叶节点插入。
- 如果最底层的节点为叶节点,将颜色的 R 、G 、B 分量累加到叶节点上,叶节点的像素数量加 1 。
- 如果叶节点的数量超过 n ,则将颜色相近的叶节点进行归并,保证叶节点的数量不超过 n 。
- 图像读取完后,对八叉树进行遍历,得到 n 个叶节点组成的颜色表。
- 再对图像进行处理,找到每个像素颜色值对应的叶节点索引,得到一个新的图像文件。
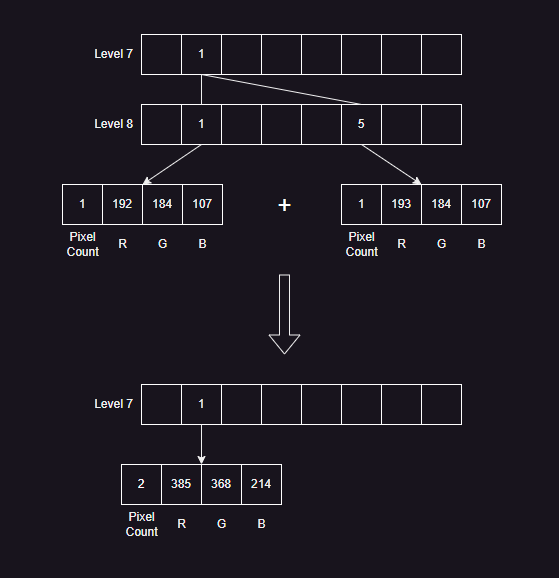
- 读取图像的每个像素,如果叶节点的数量不大于设定的颜色数量上限 n ,根据颜色沿着八叉树向下查找,则将颜色插入到八叉树中。
- 如上图所示,归并的步骤为:
- 从倒数第二层开始向上查找,找到一层有子节点的。
- 将该层中第一个包含子节点的节点,进行合并。
- 将每个子节点的 R 、G 、B 分量分别累加,设置到当前节点的 R 、G 、B 分量上。
- 将每个子节点的像素数量累加,设置到当前节点的像素数量上。
- 将当前节点设置为叶节点。
网格表面上色
- 一般情况下,网格表面的颜色是通过将网格参数化后,得到 2D 的 uv 信息,再从纹理中读取对应颜色。如果要编辑颜色,参数化过程同样不可少。然而,对于一些复杂的网格,参数化过程同样会比较复杂。通过使用八叉树结构,则可以不需要进行网格参数化,对网格表面进行上色。
建立八叉树
- 八叉树的建立过程为:
- 计算物体的包围盒,将最长的维度映射到 [0, 1] ,将三个维度都进行缩放,得到立方体,保证每一维度的分辨率一致。
- 确认上色分辨率,即确认八叉树中叶节点的深度,如 512 分辨率,则叶节点的深度为 9 。
- 细分立方体,得到八个子节点,对于与物体表面相交的节点,则继续细分。
- 直到叶节点为空或达到选择的深度,则停止细分。
上色
- 上色工具类似画刷,包括中心点坐标和半径。
- 上色的流程主要为,检查八叉树与上色工具相交的叶节点,更新叶节点颜色信息,新的颜色按照原先颜色和画刷颜色加权计算。
渲染
- 纹理网格的渲染流程主要为:
- 顶点坐标未变换时即存储为 3D 纹理坐标,光栅化过程中,通过插值得到每个片元的坐标,在片元着色器中可以得到对应的 3D 纹理坐标。
- 通过纹理坐标,查找八叉树即可得到对应的颜色。
- 然而,通过查找节点的方式,只能得到最接近的节点颜色值,为了得到高质量的结果,还需要使用线性插值和 mipmapping 技术。
- 线性插值
- 为了得到更加真实的颜色结果,每个坐标对应的颜色,需要使用相邻的 8 个节点进行插值。然而,在八叉树结构中,只会记录与物体表面相交的节点信息。对于一个坐标 (x, y, z) ,需要进行插值的 8 个节点为 (x ± 1, y ± 1, z ± 1) ,如果坐标处于边界附近,这 8 个用于插值的节点不一定都存在于八叉树中,则会导致渲染结果走样。
- 为了保证用于插值的节点都处在八叉树内,则需要扩大测试节点是否与物体表面相交的包围盒,该包围盒包含每个维度的前一个样本,即对于坐标 (x, y, z) ,其包围盒则包括 (x (- 1), y (- 1), z (- 1)) 。
- mipmapping
- 当一个纹理网格在屏幕上变小时,多个样本将落入同个像素,此时需要使用 mipmapping 技术来避免失真。
- 八叉树纹理的 mipmap 等级,最精细层(第 0 层)对应八叉树的的叶节点,往后的粗糙层是通过合并上一层的叶节点得到的,节点颜色为所有叶节点的平均值。

- 如果每个 mipmap 层都存一棵树,如上图所示,则代价会比较大。因此需要使用间接池 + LOD 池的方式。
- 间接池即一个 8 位的 RGBA 3D 纹理,其中的每个像素称作单元。间接池被细分为简介栅格,即由 2 x 2 x 2 个单元组成的立方体,树的每个节点都由一个间接栅格表示。每个间接栅格的单元可以为:
- 如果没有相应的子节点,则为空。
- 如果相应的子节点为叶节点,则为颜色数据。
- 如果相应的子节点为另一个内节点,则为一个间接栅格的索引。
- LOD 池即对应间接池的每一个栅格,存储栅格作为 mipmap 层叶节点时的颜色。
八叉树纹理转换成标准 2D 纹理
- 八叉树纹理,对于纹理创作的应用,性能表现较好。然而,对于显示复杂场景的应用,渲染的性能较低,而 GPU 可以非常高效地显示过滤后的标准 2D 纹理。因此,需要将八叉树纹理转换成标准的 2D 纹理,其步骤主要为:
- 将网格参数化。
- 使用网格顶点的三维坐标,作为纹理坐标查找八叉树。
- 查找结果即为 uv 坐标对应的颜色,则能生成对应的 2D 纹理。
- 然而,使用这种方法会产生走样,因为纹理过滤的线性插值采样到了 2D 三角形的区域之外。并且,在越粗糙的 mipmap 层,用到更多外部点,因此不能靠增加边界像素点解决。
- 为了解决这种问题,需要使用 push-pull 的外推方法,主要流程为:
- 按照前面步骤生成 2D 纹理。
- 将背景的 alpha 设置为 0,三角形用 alpha 值为 1 来渲染。
- 用 GPU 自动生成多层次纹理。
- 从最粗的层开始,把纹理所有层次合并到一个纹理上,alpha 作为透明的系数,即当前像素颜色 = 当前层采样的颜色 + 缓冲区颜色 * (1 - 当前层采样颜色透明度) 。