Algorithm

空间数据结构 — k-D Tree

Posted by Xun on Monday, June 5, 2023

K-Dimensional Tree

简介

  • KD 树（K-Dimensional Tree）是一种多维的二叉搜索树，其中 k 代表空间维度。这种结构有一个优点，就是能高效地处理多种类型的查询。经验证，该结构的平均运行时间如下：
    • 插入节点：O(log n) 。
    • 删除根节点：O(n^[(k-1)/k]) 。
    • 删除随机节点：O(log n) 。
    • 优化树结构（保证对数搜索性能）：O(nlog n) 。
    • 搜索 t 个维度指定值（最大时间）：O(n^[(k - t)/k]) 。
    • 最近邻搜索（平均时间）：O(log n) 。
  • 可以看出，对于二维场景，在查找一个最接近的对象时，穷举法查找的耗时为 O(n) ，而 kd 树的平均耗时为 O(log n) ，即便是最差的情况下的耗时也仅为 O(n^(1/2))，查找效率都是非常可观的。

构建树

  • 构建树的主要流程如下：
    • 确定一个主维度，找出所有点在这个维度下的中位数。
    • 将中位数对应的点设为节点，按当前维度划分为两个子空间。
    • 将当前维度下的所有点分为两组，小于中位数的为左子树，大于中位数的为右子树。
    • 按照下一个维度，分别对左子树和右子树重复上述步骤进行构建，直到所有点都设为节点。
  • 对于一组点 A(60, 50) 、B(30, 45) 、C(75, 60) 、D(10, 30) 、E(45, 55) 、F(85, 40) 、G(80, 70) ，构建流程如下：
    • 取 x 为主维度，则中位数为 A(60, 50)，将空间划分为左右两个，左子树为 B(30, 45) 、D(10, 30) 、E(45, 55) ，右子树为 C(75, 60) 、F(85, 40) 、G(80, 70) 。
    • 取 y 为主维度，则左子树中位数为 B(30, 45) ，右子树中位数为 C(75, 60) ，将各自空间划分为上下两个。
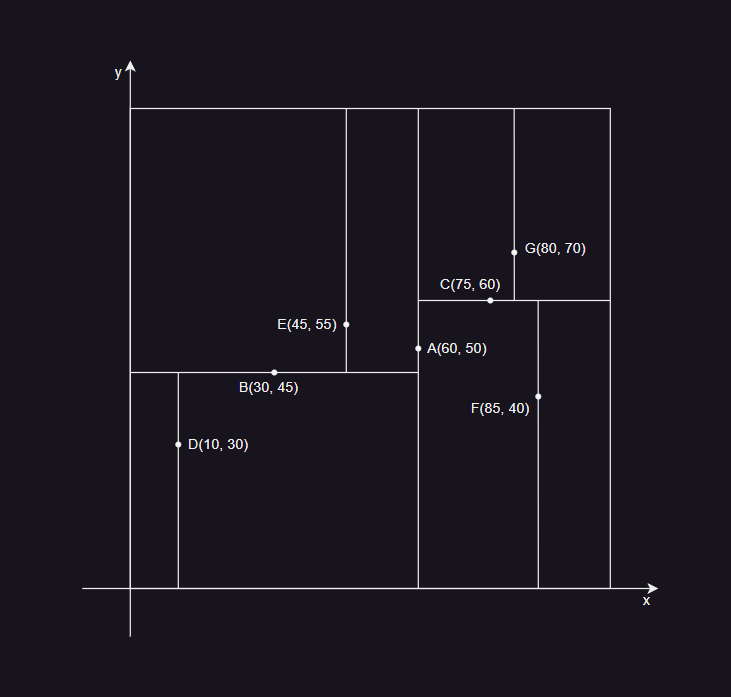
    • 取 x 为主维度，将 D、E、F、G 都进行空间划分。 KDTree_1.png
  • 查找中位数的算法，有最差为 O(n) 的实现，将数据进行分组也是需要 O(n) ，树的深度为 log n ，所以构建树的时间复杂度为 O(nlog n) 。
  • 确定主维度，通常使用计算各个维度下的数据方差，取数据方差大的维度作为主维度进行空间划分。数据方差大表示数据在当前维度上相对分散，在该维度上划分可以得到较好的结果。

插入节点

  • 插入节点的主要流程为：
    • 检查根节点是否为空。
      • 如果根节点为空，则将新节点设置为根节点，将左子树和右子树设为空，将当前维度设为 0 ，返回空节点。
      • 如果根节点不为空，设置当前节点为根节点。
    • 检查新节点和当前节点是否相同。
      • 如果当前节点和新节点相同，即从 0 ~ k - 1 维的值都相同，则新节点无需插入，返回当前节点。
      • 如果当前节点和新节点不同，则需要从当前节点的维度 j 起，判断是往左子树检查还是往右子树检查。
        • 如果新节点在此维度下的值小于当前节点，则返回左子树。
        • 如果新节点在此维度下的值大于当前节点，则返回右子树。
        • 如果新节点在此维度下的值等于当前节点，则取下一个维度（j + 1）% k，重复上述判断。
    • 检查子节点是否为空。
      • 如果子节点为空，则将新节点设置为子节点所在的子树位置，将左子树和右子树设为空，将当前维度设置为父节点的下一个维度，返回空节点。
      • 如果子节点不为空，则设置子节点为当前节点，递归执行检查新节点和当前节点是否相同。
  • 由于插入的每一个数据是随机的，即概率上左右子树的分布都是相同的，所以插入后的 kd 树通常为平衡二叉树，即树高为 log n ，因此插入通常在 O(log n) 下就可以完成。
  • 对于破坏性非随机插入节点时，会导致树出现不平衡，就需要在插入完成后对树进行优化，即重新构建树。

部分匹配查询

  • 对于一棵维度为 k 的 kd 树，当给定 t 个维度（ t < k ）的指定值，查找满足这 t 个维度的节点，称为部分匹配查询。当某个维度有指定值时，如果节点在这个维度下的值小于指定值，则只需要检查左子树，否则只需要检查右子树，即只需要检查一边的子树。而当某个维度没有指定值时，则需要将左右子树都进行检查。
  • 对于一棵维度 k 为 3，高为 kh 的树，每 k 层为一级，给定维度数量 t 为 1 ，则有：
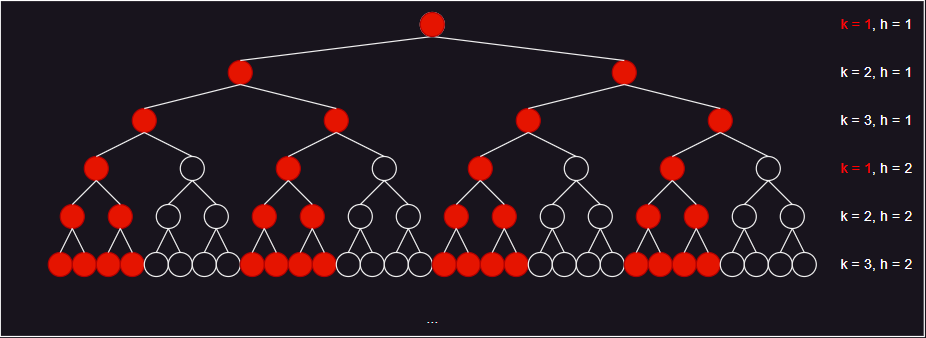
    • 当 d = 1 为指定维度，只需要检查一个节点。而 d = 2 、d = 3 为指定维度，则左右子节点都需要检查。 KDTree_2.png
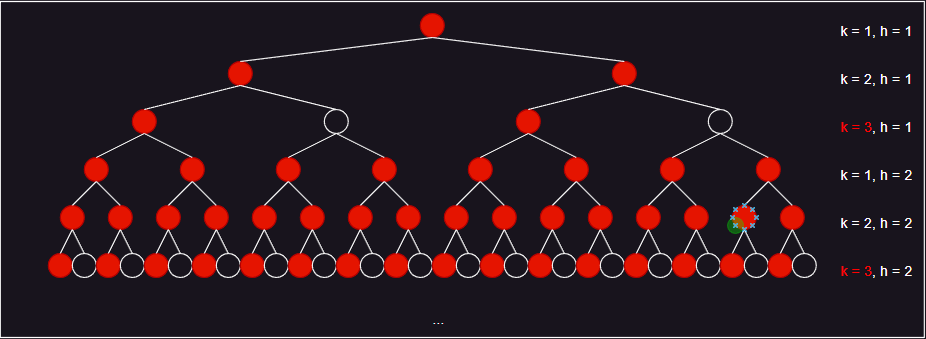
    • 当 d = 1 、d = 2 不为指定维度，则左右子节点都需要检查。d = 3 为指定维度，则只需要检查一个子节点。 KDTree_3.png
  • 可以看到，如果指定的维度在前，则每一级里每一层需要遍历的节点数量，则前 t 层是和上一级最后一层的数量一样，后 k - t 层是逐层翻倍。相反，如果指定的维度在后，则前 t 层是逐层翻倍，后 k - t 层和 t 层一样。因此，当指定的维度在 k 维中的末尾时，会有最大的遍历数量。
  • 此时，每一级需要检查的节点为 2 ^ [(h - 1) * (k - t)] + … + 2 ^ [(h * (k - t) - 1] + t * 2 ^ [(h * (k - t) - 1] ，可以得到查询的总代价为 cn ^ [(k - t) / k] ，即 O(n^[(k - t)/k]) 。

删除节点

  • 删除节点的主要流程为：
    • 检查删除的节点 P 是否为叶节点（左右子树都为空）。
      • 如果删除的节点 P 为叶节点，则直接删除，返回空。
      • 如果删除的节点 P 不为叶节点，设置当前维度为删除的节点 P 的维度。
    • 检查删除的节点 P 的后继者节点。
      • 如果删除的节点 P 的右子树不为空，则找出当前维度右子树下的所有节点和节点 P 距离最小的节点 Q 。
      • 如果删除的节点 P 的右子树为空，则找出当前维度左子树下的所有节点和节点 P 距离最大的节点 Q 。
    • 按上述流程执行删除节点 Q ，将返回值设置到节点 Q 所在的位置。
    • 设置节点 Q 的维度为节点 P 的维度，设置节点 Q 的左右子树为节点 P 的左右子树，设置节点 Q 到节点 P 的位置，删除节点 P 。
  • 由于删除节点时需要查找子树中的后继者节点，所以存在代价上限为子树中的节点数量。也就是说，对于节点数量为 n 的 kd 树，删除某个节点的平均代价为所有节点的代价平均值，即所有节点的子树中的节点数量之和 / n 。由于节点是随机分布的，所以树通常为平衡二叉树，则树高为 log n ，所有节点的子树节点数量总和为 n log n ，因此随机删除节点的平均时间复杂度为 O(log n) 。
  • 删除节点的后继者节点查找操作，和部分匹配查询类似，即指定一个节点维度对应的值进行查找。因此，删除根节点的时间复杂度为 O(n^[(k - 1)/k]) 。
  • 当删除的节点不是随机时，同样会导致树出现不平衡，就重新构建树来保证平衡性。

最近邻查询

  • 最近邻查询，即在 kd 树中，查找和指定坐标点最近的节点，主要流程为：
    • 如果根节点为空，则返回空。
    • 初始化当前节点和最近节点为根节点，创建一个查询栈，向下查询，直到查询到叶节点。
      • 将当前节点压入查询栈中，设置当前维度为当前节点的所属维度。
      • 如果最近节点到目标点的距离，大于当前节点到目标点的距离，则将当前节点设置为最近节点，将对应距离设置为最小距离。
      • 在当前维度下，如果目标点的值不大于当前节点，则设置当前节点为当前节点的左子节点，否则设置当前节点为当前节点的右子节点。
      • 如果当前节点不为空，则重复进行上述步骤。
    • 回溯检查，对查询栈进行检查。
      • 从查询栈中取出栈顶节点作为回溯节点，设置当前维度为回溯节点的所属维度。
      • 如果目标点和回溯节点之间在当前维度下的距离小于最小距离，则：
        • 在当前维度下，如果目标点的值不大于当前节点，则设置当前节点为回溯节点的右子节点，否则设置当前节点为当前节点的左子节点，即检查未检查过的另一侧子树。
        • 将当前节点压入查询栈中。
        • 如果最近节点到目标点的距离，大于当前节点到目标点的距离，则将当前节点设置为最近节点，将对应距离设置为最小距离。
      • 如果查询栈不为空，则重复进行上述步骤。

时间复杂度推导

  • 查询树的过程，和插入节点的类似，从根节点到叶节点，可以在 O(log n) 内完成，而回溯过程则相对比较复杂。
  • 回溯过程的部分参数说明如下：
    • N ：kd 树的节点数。
    • k ：树的维度。
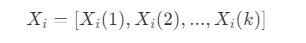
    • X_i ：第 i 个节点的值，即 X_i = [X_i(1) , X_i(2), … , X_i(k)] 。 Math_KDTree_1.png
    • X_q : 要查询的目标节点 q 。
    • X_m ：kd 树中离目标点第 m 近的节点。
    • b ：叶节点中包含的节点数。
    • D(X, Y) ：X 和 Y 的距离。
    • p(X) ：X 的概率分布。
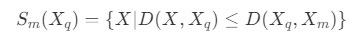
    • S_m(X_q) ：X_m 节点到 X_q 节点的最小距离在所有维度上形成的超平面球，即 Math_KDTree_2.png
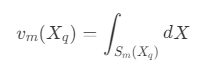
    • v_m ：S_m(X_q) 的包围盒的体积，即 Math_KDTree_3.png
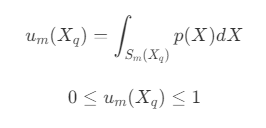
    • u_m ：满足 S_m(X_q) 的所有 X 的概率，即 Math_KDTree_4.png
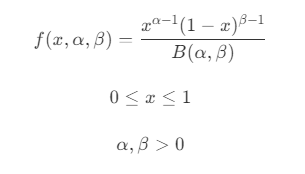
  • 由于 X 只有在范围内和不在范围内的两种结果，所以可以使用 Beta 分布模型来代替，即 Math_KDTree_5.png
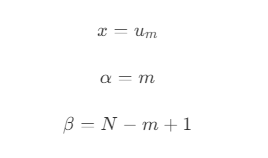
  • 对应当前参数，则有 Math_KDTree_6.png
  • 由于 X_m 是处在边界上，在这里归进了范围内，所以导致了范围内和范围外的概率不对称，因此对范围外加 1 ，从而能更加准确模拟在二分查找中的期望时间。
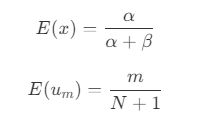
  • Beta 分布的期望公式为 Math_KDTree_7.png
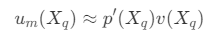
  • 当 N 足够大，S_m(X_q) 足够小时，概率 p(X) 近似为常数，则有 Math_KDTree_8.png
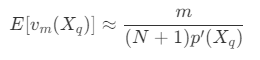
  • 其中，p'(X_q) 为 S_m(X_q) 的平均概率，所以不会为 0 ，因此有 Math_KDTree_9.png
  • 对于一棵平衡的 kd 树，空间被划分成多个 k 维的超立方体，边长为超立方体体积的 k 次方根，每个超立方体包含几乎相同数量的节点，因此，空间上的每个最小的超立方体的期望体积为 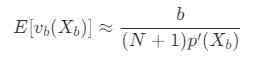Math_KDTree_10.png b 代表超立方体中的节点数，X_b 为定位该超立方体的节点。
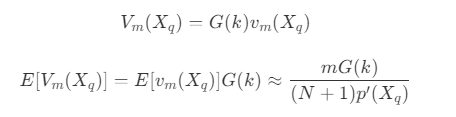
  • 设 V_m(X_q) 为 kd 树中包围 S_m(X_q) 的父级超立方体，其体积和 v_m(X_q) 成比例，比例常数为 G(k) ，比例常数取决于相异度度量和维度，可以得到 Math_KDTree_11.png
  • V_m(X_q) 中的包含的最小超立方体 v_b(X_b) 数量为体积的商，此时最接近 X_q 的节点一定被包含在 V_m(X_q) 的所有相邻最小超立方体组成的范围内，所以通过边长计算范围，得到平均数量上限 L' 为 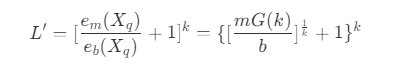Math_KDTree_12.png 其中，e_m(X_q) 为 V_m(X_q) 的边长，e_b(X_q) 为相邻的最小超立方体，相除后向上取整，k 次方得到体积，概率 p(X) 近似相等。
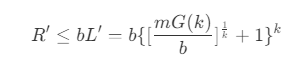
  • 此时，上限 L 由于每个最小超立方体中包含的节点数量为 b ，则需要遍历的节点平均数量上限 R' 为 Math_KDTree_13.png
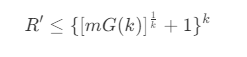
  • 当 b = 1 时，即每个最小立方体只包含一个节点时，则有 Math_KDTree_14.png
  • 可以看到，此时需要遍历的平均节点数量和 N 无关，只和维度 k 相关，即为 k 相关的常数，所以最近邻查询的平均时间复杂度整体为 O(log n) 。

K 近邻查询（KNN)

  • K 近邻查询，即在 kd 树中，查找和指定坐标点第 K 近的节点，主要流程为：
    • 如果根节点为空，则返回空。
    • 初始化当前节点和最近节点为根节点，创建一个查询栈，以及一个 K 节点的最大堆，初始化根节点为距离为 ∞ ，向下查询，直到查询到叶节点。
      • 将当前节点压入查询栈中，设置当前维度为当前节点的所属维度。
      • 如果堆的根节点的距离，大于当前节点到目标点的距离，则将对应距离插入最大堆中。
        • 如果堆的节点数量小于 K ，则直接插入插入新的距离节点。
        • 如果堆的节点数量大于等于 K ，则取出根节点，再插入新的距离节点。
      • 在当前维度下，如果目标点的值不大于当前节点，则设置当前节点为当前节点的左子节点，否则设置当前节点为当前节点的右子节点。
      • 如果当前节点不为空，则重复进行上述步骤。
    • 回溯检查，对查询栈进行检查。
      • 从查询栈中取出栈顶节点作为回溯节点，设置当前维度为回溯节点的所属维度。
      • 如果目标点和回溯节点之间在当前维度下的距离小于堆的根节点距离，则：
        • 在当前维度下，如果目标点的值不大于当前节点，则设置当前节点为回溯节点的右子节点，否则设置当前节点为当前节点的左子节点，即检查未检查过的另一侧子树。
        • 将当前节点压入查询栈中。
        • 如果堆的根节点的距离，大于当前节点到目标点的距离，则将对应距离插入最大堆中。
      • 如果查询栈不为空，则重复进行上述步骤。
  • 可以看到，当 K = 1 时，K 近邻查询即为最近邻查询，前面分析最近邻查询的平均时间复杂度为 O(log n) 。K 近邻查询多了一个最大堆的维护，由于 K 为常数，当 K 较小时，可以认为每次维护最大堆只需要 O(1) 的代价，则查询和回溯的过程中维护最大堆的代价为 2 * O(log n) ，因此 K 近邻查询的平均时间复杂度也为 O(log n) 。

BBF(Best-Bin-First) 查询

  • 当数据是高维时，任何查询都可能导致大部分节点都要被访问和比较，搜索效率会下降并接近穷尽搜索。通常需要满足 N » 2^k ，才能达到高效的搜索。经测试，使用 kd 树时的维度应该保证 k <= 20 。当维度较大时，可以采用 BBF(Best-Bin-First) 查询机制来进行优化。BBF 对最近邻查询的改进主要有：
    • 将回溯的栈结构修改为最小堆结构。
    • 增加运行超时限定。
  • 最小堆结构，能保证优先处理回溯列表中距离最近的点，而超时限定能保证把查询时间控制在要求的时间内。然而这种方式得到的结果是近似的，并非准确的最近邻，但能在高维度下有较好的查询效率。

总结

  • kd 树在查询上，具有 O(log n) 的平均时间，和穷举法相比，有很大的效率提升。同时，对于多种复杂的搜索条件，也能有较好的查询效率。然而，对于非静态的数据，增删节点修改树的过程，会破坏树的平衡性，失去树原有的优势，此时需要重建树来恢复树的平衡。但重建树的代价较大，如果频繁重建树，则查询的耗时会增加建树的时间，从而导致效率下降。因此，应用过程需要根据实际场景进行评估，尽可能控制重建的频率。

参考

CATALOG