Algorithm

空间数据结构 — BVH

Posted by Xun on Thursday, June 1, 2023

BVH（Bounding Volume Hierarchiy）是基于边界体积 (BV) 的结构，通过使用简单的几何形状，代替各种复杂的对象，从而加速检测效率。

简介

  • BV（Bounding Volume），边界体积，即一个包含了一些物体的几何结构。由于场景的物体存在各种样式，做一些检测工作时，如相交性测试，需要对每种复杂的结构进行特殊处理，对复杂结构的计算成本也相对较高。然而很多时候经常没有出现相交，甚至和物体有较大的距离，此时仍然使用复杂的计算会导致整体效率低下。BVH 的基本思路是，使用简单的包围盒结构，代替原有的复杂结构，并对物体进行分组，从而简化计算过程，提升效率。

包围盒

  • 常见的包围盒有：
    • 球（sphere）
    • 轴对齐包围盒（AABB，axis-aligned bounding box）
    • 离散定向多面体（k-DOP，discrete oriented polytopes)
    • 定向包围盒（OBB，oriented bounding box）
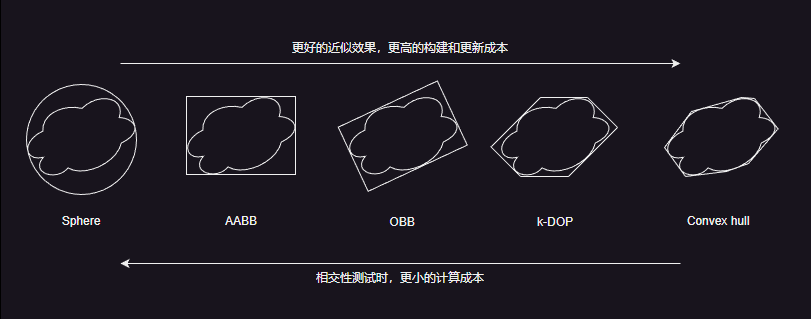
    • … BVH_1.png
  • 越是复杂的包围盒，能有更好的近似效果，当然代价就是更高的构建和更新成本。为了达到加速计算的效果，通常需要选择计算量较小的结构。由于 AABB 包围盒的轴与坐标轴相同，便于进行计算，因此通常会使用 AABB 包围盒来作为加速结构。

目标

  • 使用 BVH ，是为了减少检测的过程中的检查次数，从而提高效率，因此需要最终构建出来的 BVH 达到以下目标：
    • 平衡树。
    • 所有包围盒都是紧凑的。
    • 具有最小的冗余（即在树的每一层，对象分布在一个以上的包围盒中）。

层级构建

  • 构建层级的方案有：
    • 自底向上
    • 自顶向下
    • 插入式

自底向上

  • 自底向上的构建流程为：
    • 对每个对象创建其包围盒。
    • 将一定数量的包围盒组合起来，创建一个新的包围盒。
    • 递归对新的包围盒和原始包围盒进行分组，重复上一步。
    • 当层级只有一个包围盒时，完成构建。
  • 为了得到高质量的 BVH 结构，通常使用层次聚类算法（Agglomerative Clustering），主要步骤为：
    • 分别计算每个包围盒与其他所有包围盒的距离。
    • 比较所有的距离，找出其中最小距离的两个包围盒。
    • 将最小距离的包围盒组成一个新的包围盒，重复上面的步骤。
  • 上述实现方式为 O(N^3)，该算法同样有 O(N^2) 的实现，但核心思路是一致的。

自顶向下

  • 自顶向下的构建流程为：
    • 对整体对象创建包围盒。
    • 根据启发式方法，递归分离对象和创建包围盒。
    • 当所有包围盒在当前层级只包含小于 n 个对象时，完成构建。
  • 划分子节点，通常根据包围盒最长的边来划分，对于 AABB ，找到包围盒的距离最长一对平面，经过包围盒的中心且平行于这对平面进行划分。尽管这个方法看起来非常简单，但该方法已经被证明，它是高效的，并且能生产平衡树，仅仅一秒钟可以完成包含数千个多边形对象的完整层次设置，同时允许将对象动态添加到场景中。

插入式

  • 插入式的构建流程为：
    • 为新插入的叶子节点，找到最好的兄弟节点。
    • 创建新的父节点。
    • 沿着树往回重新调整包围盒。
表面积启发式（Surface Area Heuristic，SAH）
  • 表面积启发式是一个有力的指标，用于构建 BVH ，核心思想是，光线击中物体的概率与物体的表面成比例，也就是说，当包围盒越紧凑，其表面积越小，光线相交的概率就越小，检测过程就越不容易出现假相交。因此 BVH 的构建过程中，当插入一个新的节点时，需要选择一个节点，使得增加的新的包围盒表面积是最小的，即整棵树的代价是最小的。
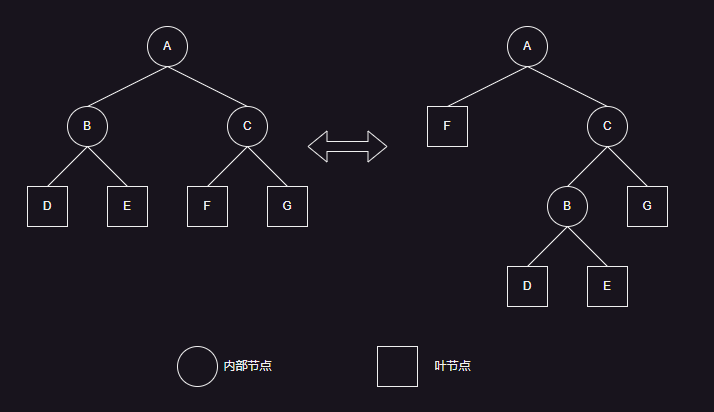
  • 对于相同的叶节点，构成的 BVH 树的根节点也是一样的，但是内部节点可以有不同的组合。 BVH_2.png
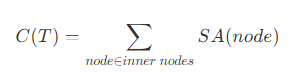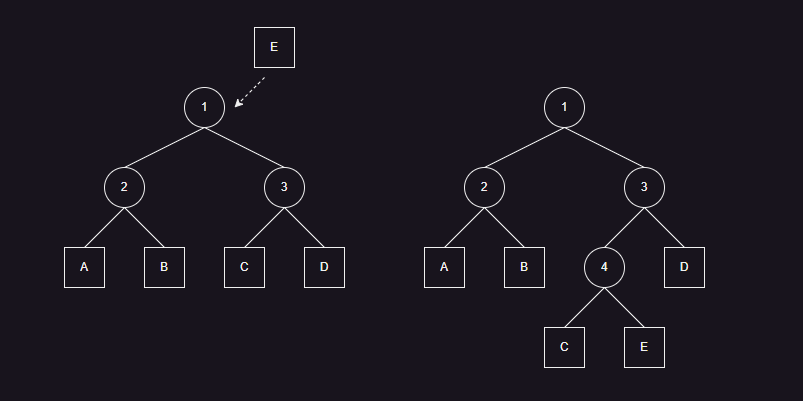
  • 如上图所示，尽管根节点和叶节点相同，但是两棵树的代价是不一样的，也就是说，相同叶节点组成的树，其差别主要由内部节点决定，和叶节点的代价无关，因此树的代价 C(T) 可以定义为 Math_BVH_1.png 其中，SA(node) 代表内部节点 node 的代价，以 AABB 为例，即为 AABB 的表面积。 BVH_3.png
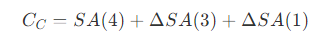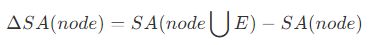
  • 如上图所示，当插入一个节点 E 时，需要找到插入到各个位置中最小的代价。而插入节点后的新树，增加的代价为每一层的内部节点表面积的增量和。假设节点 E 插入到节点 4，则增加的代价为 Math_BVH_2.png 其中，△SA(node) 即内部节点表面积的增量，为原节点和新节点组成的新的包围盒，与原节点包围盒相比的表面积增量。 Math_BVH_3.png
  • 然而，对于具有 n 个叶节点的树，节点数量为 2n - 1 。如果要插入一个新节点，就要计算 2n - 1 个节点的增加代价，从中找出代价最小的节点进行插入。显然，计算所有节点的插入方式成本较高，因此引入一种更快的全局搜索方式，分支边界算法。
分支边界算法（Branch and Bound Algorithm）
  • 插入到某个节点产生的代价，分为两部分：
    • 直接代价：对找到的兄弟节点创建父节点，产生新的内部节点的表面积，即 SA(4 ∪ E) 。
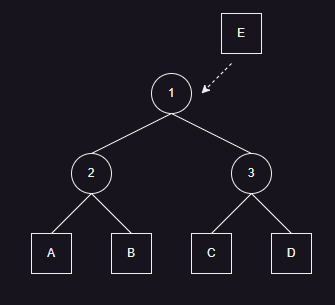
    • 继承代价：由于调整各个祖先节点的包围盒而增加的表面积，即 △SA(3) ＋ △SA(1) 。 BVH_4.png
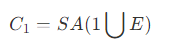
  • 如上图所示，插入节点 E ，假如插入位置为节点 1 ，则产生的代价为 Math_BVH_4.png
  • 此时需要递归向下检查子节点 2 和节点 3 ，假如插入位置为节点 2 ，则
    • 当节点 E 的包围盒在节点 2 的包围盒内时，新的内部节点的包围盒即为节点 2 的包围盒。
    • 当节点 2 的包围盒在节点 E 的包围盒内时，新的内部节点的包围盒即为节点 E 的包围盒。
    • 当节点 2 的包围盒与节点 E 的包围盒相交时，新的内部节点的包围盒即为节点 E 和节点 2组合的包围盒。
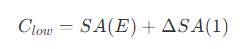
  • 因此可以看出，节点 E 的表面积即为新内部节点的最小表面积，即插入的直接代价下限为 SA(E) ，因此子节点代价的下限值为 Math_BVH_5.png
  • 而对于子节点的子节点，直接代价的下限同样是 SA(E) ，而继承代价则会增加子节点包围盒修改增加的表面积，因此子节点代价的下限值即为下层节点的代价下限值。
  • 如果子节点代价的下限值，小于当前最小代价，则记录当前最小代价，并将子节点加入检查队列，继续向下检查。
  • 然而，如果当前最小代价，小于子节点代价的下限值，那么子节点则不需要再继续检查，从而可以减少多余的检查。
移动物体策略
  • 对于移动物体，有几种处理方式
    • 修改祖先包围盒。
    • 重建子树。
      • 代价很高，就像垃圾回收一样。
    • 移除并重新插入。
      • 代价同样很高，但是是分散的。
  • 其中，修改祖先包围盒会导致树的质量边低。重建子树的代价很高，就像垃圾回收一样。移除并重新插入的代价同样很高，但是是分散的，因此通常选择这种方式。
  • 由于物体并不经常每帧都移动较大的距离，因此可以采用扩大的 AABB ，只有当物体贴紧的 AABB 超出扩大的 AABB 时，才更新叶节点。生成扩大的 AABB 方式有很多种，可以根据实际情况自行选择。
树旋转
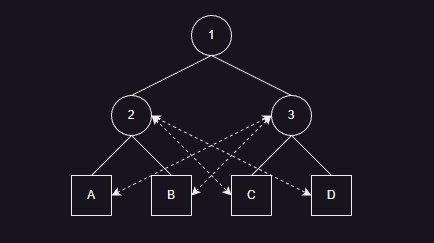
  • 树旋转用于 AVL 树以保持它们的平衡，也可以用于 BVH 以减少表面积并减少排序输入引入的不平衡问题。 BVH_5.png
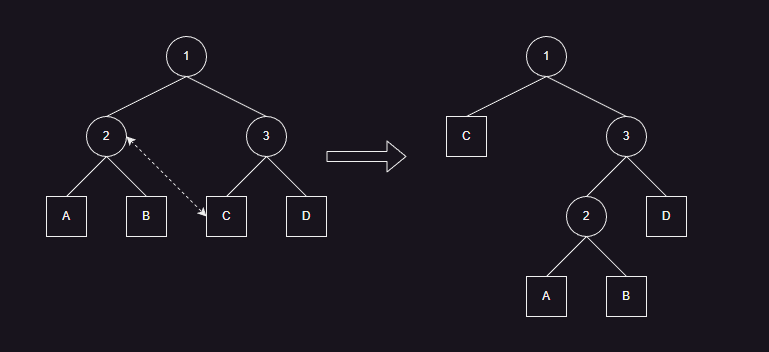
  • 树旋转主要是与其父节点的兄弟节点交换，交换完成后，不会对上层和下层节点产生影响。 BVH_6.png
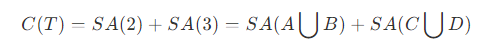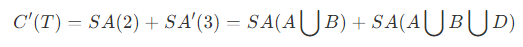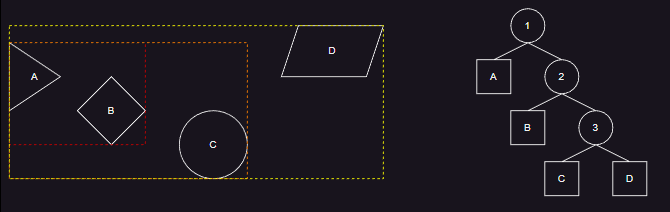
  • 如图所示，节点 2 和节点 E 交换后，上层节点 1 以及下层节点 A 、B 、C 、D 都不会发生变化。旋转前，树的代价为 Math_BVH_6.png 旋转后，树的代价为 Math_BVH_7.png 当旋转后的代价比原来小时，则可以改善树的结构。 BVH_7.png
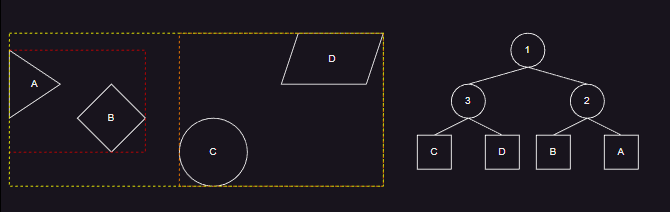
  • 如上图对象 A 、B 、C 、D 是从左到右排序好的，当逐一插入时，就会出现链表的结构，失去了 BVH 加速的作用。 BVH_8.png
  • 当插入节点 D 后，对插入位置 3 的父节点的兄弟节点，进行树旋转检查，发现代价减小，从而调整了树的结构，保持了 BVH 的树平衡性。

应用

  • BVH 通过是用体积近似、几何特征简单的包围盒，来近似描述复杂的几何对象，并通过构造树状层次结构，逐层接近真实的几何对象，从而减少了中间大量的复杂计算，通常用于光线追踪、视锥裁减等，在三维场景的渲染中，是非常常用的结构。

光线追踪

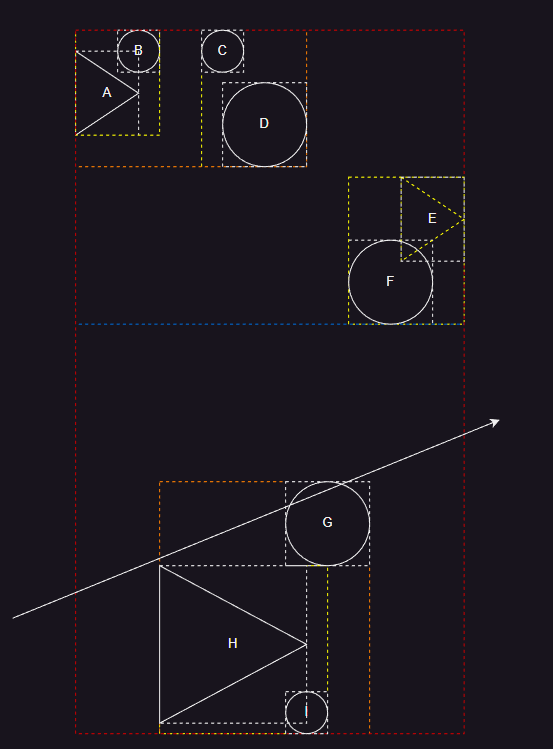
  • 对于场景中的对象，如果要求光线是否与物体相交，则需要对场景中的对象逐一遍历，当场景的对象比较复杂，并且数量较多时，显然效率低下。 BVH_9.png
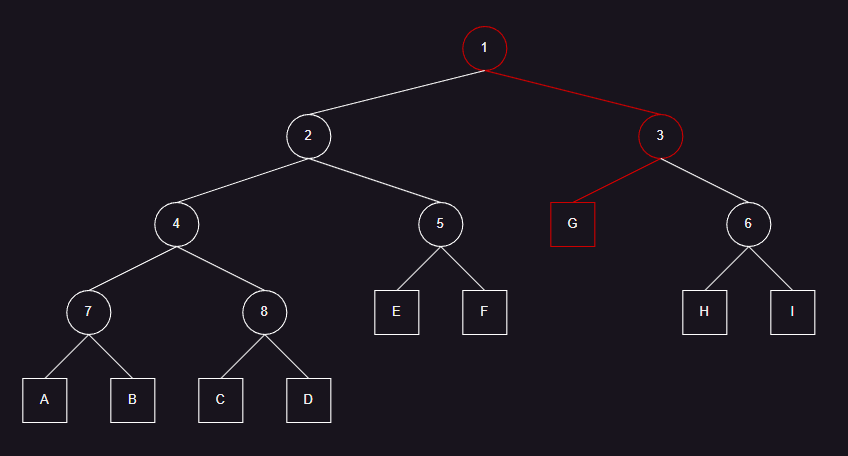
  • 通过构建 BVH ，从每个物体开始，生成 AABB 包围盒，并逐层构建，最终组成一棵树。 BVH_10.png
  • 此时，求光线与物体是否相交，如上图所示，步骤为：
    • 检查光线与包围盒 1 是否相交。
    • 光线与包围盒 1 相交，检查包围盒 2 、包围盒 3 是否与光线相交。
    • 光线与包围盒 2 不相交，与包围盒 3 相交，检查包围盒 G 、包围盒 6 是否与光线相交。
    • 光线与包围盒 G 相交，与包围盒 6 相交，检查物体 G 是否与光线相交。
    • 光线与物体 G 相交。
  • 整个过程，进行了 4 次光线与 AABB 包围盒求交，和 1 次光线与几何物体求交。不采用 BVH 结构时，则需要进行 9 次光线与几何物体求交。因此 BVH 通常能得到较好的加速效果。

视锥裁剪

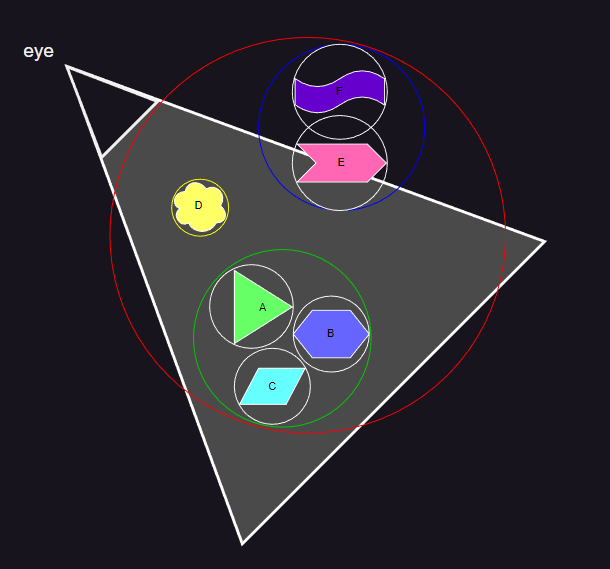
  • 相比光线和物体求交，视锥裁剪需要检查哪些物体在视锥体范围内，即需要对几何体和几何体求交，复杂度会更高。同样，如果需要逐一检查，计算量会非常大。 BVH_11.png
  • 如上图所示，视锥体灰色部分为可见范围，构建包围盒后，检查步骤为：
    • 检查视锥体和红色圆是否相交。
    • 视锥体和红色圆相交，分别检查绿色圆、黄色圆、蓝色圆与视锥体是否相交。
    • 绿色圆、黄色圆与视锥体相交，且在视锥体内部，则 A 、B 、C 、D 都在视锥体内部，蓝色圆与视锥体相交，检查 E 、F 是否与视锥体相交。
    • E 与视锥体相交，F 在视锥体外。
  • 可以看到，当包围盒在视锥体内部时，后续的子节点则不需要再进行计算。包围盒在视锥体外部时，也不再需要计算视锥体和真实物体的复杂几何求交。只有包围盒部分在视锥体内时，才需要对物体的真实范围进行求交计算。同样，可以看到 BVH 能得到很好的表现。

参考

CATALOG