标量量化(Scalar Quantization)是数字信号处理中一个基本而重要的概念,它在数据压缩和信号表示方面发挥着关键作用。
简介
- 游戏开发过程中,数据读取和存储必不可少的环节,通常会要求读取的速度要快。然而,对于数据量较大的情况,还会对数据大小进行考量。尤其是在移动设备上,数据文件大小不仅影响安装包的大小,同时还会影响内存的占用大小。因此,开发者通常会对数据进行一定程度的调整,增加量化的过程,将多个数据合并成一个,读取时再对其进行解码,从而实现对数据的压缩。
- 将一组连续的实数映射到一组整数,这个过程称为量化。通过一组间隔将数据进行划分,并为每个间隔分配一个整数值来进行量化。而当需要解码时,将每个整数映射回表示间隔的标量值。
整数量化
- 整型数据在内存中的表示为:

- 对整数进行量化往往比较简单,通常会以二进制或十进制格式进行处理。例如:
- 有个大小为 1024 x 1024 的地图,每个格子有 2 种加成效果,每种加成效果有不同的数值。
- 1-攻击加成 :0 ~ 99
- 2-防御加成 :0 ~ 99
- 3-速度加成 :0 ~ 99
- 4-生命加成 :0 ~ 99
- 为了存储整个地图的每种加成数据,需要一个二维数组,即:
uint[][] buff1 = new uint[1024][1024];
uint[][] buff2 = new uint[1024][1024];
uint[][] buff3 = new uint[1024][1024];
uint[][] buff4 = new uint[1024][1024];
for(int y = 0; y < 1024; y++)
{
for(int x = 0; x < 1024; x++)
{
buff1[x][y] = 90;
buff2[x][y] = 80;
buff3[x][y] = 70;
buff4[x][y] = 60;
}
}
- 可以看到,整个地图的加成数据,使用的 uint 大小为 1024 * 1024 * 4 * 4 / 1024 / 1024 = 16 MB 。为了对数据进行压缩,可以进行量化,量化方式可以以十进制或者二进制方式进行。
十进制
- 以十进制量化,相对比较直观,由于加成值为 0 ~ 99 ,可以使用每 2 位作为保存,即
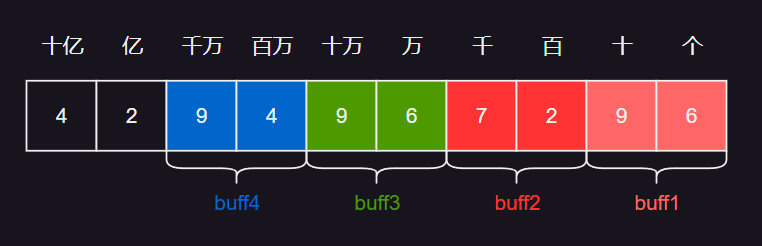
uint[][] buff = new uint[1024][1024];
for(int y = 0; y < 1024; y++)
{
for(int x = 0; x < 1024; x++)
{
buff[x][y] = buff1[x][y] * 100 ^ 0 + buff2[x][y] * 100 ^ 1 + buff3[x][y] * 100 ^ 2 + buff4[x][y] * 100 ^ 3
}
}
- 十进制的每两位用于保存一个 buff 加成数据,读取的时候再根据 buff 所在的位进行读取,例如,buff2 使用百位和千位记录,则读取方式为:
int x = 100;
int y = 100;
uint buff2_100_100 = buff[100][100] % 10000 / 100;
二进制
- 二进制量化,和十进制量化类似,也是按位进行划分,使用每 8 位保存一个数据,即

uint[][] buff = new uint[1024][1024];
for(int y = 0; y < 1024; y++)
{
for(int x = 0; x < 1024; x++)
{
buff[x][y] = buff1[x][y] | (buff2[x][y] << 8) | (buff3[x][y] << 16) | (buff4[x][y] << 24)
}
}
- 二进制的每八位用于保存一个 buff 加成数据,范围为 0 ~ 127,读取方式为:
int x = 100;
int y = 100;
uint buff2_100_100 = buff[100][100] & (127 << 8);
浮点数量化
内存表示
- 浮点型数据的在内存中的表示为:


- 相比与整型,浮点型将值分为指数部分和有效数字部分。
- 指数有正负,采用 The Biased exponent(有偏指数),根据 IEEE754 规定,2 ^ (e - 1) - 1 对应的的值为 0 ,其中 e 为指数的位数。大于这个值的为正数(即小数点左移),小于这个值的为负数(即小数点右移)。
- 对于单精度浮点数,2 ^ (8 - 1) - 1 = 127 为 0 。
- 对于双精度浮点数,2 ^ (11 - 1) - 1 = 1023 为 0 。
- 有效数字(significand)部分,IEEE754 规定,在二进制数中,将小数点前面的值固定为 1,因此可以省略不存,只存小数点后的数,而可以多存 1 位,这种形式的浮点数为规范化浮点数。例如:
- 十进制数 : 0.625
- 二进制数 : 0.101
- 十进制小数部分 * 2,大于 1 则当前位为 1 ,否则为 0 。继续取小数部分计算,直到小数部分为 0 。
- 转为十进制时,即每一位使用 2 ^ n 表示后进行累加,其中小数点后的 n 为负数。
- 内存中 : 0 0111 1110 0100 0000 0000 0000 0000 000
- 正数,符号位为 0。
- 小数点右移 1 位,小数点前为 1 ,指数部分为 127 - 1 = 126 ,即 0111 1110 。
- 有效数字部分,即小数点移动后,小数点后的数,即 0100 0000 0000 0000 0000 000 。
- 当数字较小时,小数部分的后面几位对整体的影响较大,随着数字的逐渐增大,影响会越来越小,有效数字中代表小数部分的位数也会越来越小,这种情况下的精度误差通常也符合实际使用需求,也能被接受。
误差
- 根据浮点数的二进制转化规则,可以发现,一个简单的十进制数,在内存中不一定能准确表示,如:
- 十进制数 : 0.1
- 二进制数 : 0.0001 1001 1001 1001 1001 1001 1001 1001 …
- 内存中 : 0 0111 1011 1001 1001 1001 1001 1001 101 (即 0.1000 0000 1490 1161 19)
- 可以看到,0.1 在二进制中的表示,是一个无限循环的数,而内存中的位数是有限的,所以超出的位数只能舍去。这也是浮点数计算中总会出现误差的根本原因。
- 假设小数部分的存储方式和整数部分一样,n 也为非负数,小数点后有限位数为 3 ,则对应二进制位数需要为 10 ,其中最后一位为 0 ,则:
- 十进制数 : 0.1
- 二进制数 : 0.0001 1001 00
- 内存中 : 0 0111 1011 0000 0000 0000 0000 0000 000
- 可以发现,在这种方式下,大部分小数都能够没有误差地表示,因为使用了乘法替代了除法,从而使得有限位数的小数部分得以连续表示,某种程度上来说,更加便于开发者理解和使用。
- 然而,随着数字的增大,当有效数字部分仅剩最后一位代表小数部分时,则有:
- 内存中 : 0 1001 0101 0000 0000 0000 0000 0000 000
- 二进制范围 :1000 0000 0000 0000 0000 000.0000 0000 00 ~ 1000 0000 0000 0000 0000 000.0111 1111 11
- 十进制范围 : 4194304.0 ~ 4194304.511
- 内存中 : 0 1001 0101 0000 0000 0000 0000 0000 001
- 二进制范围 :1000 0000 0000 0000 0000 000.0111 1111 11 ~ 1000 0000 0000 0000 0000 000.1111 1001 11
- 十进制范围 : 4194304.512 ~ 4194304.999
- 此时,内存中连续的两个值,代表了不同范围的区间,所以这种方式可能会导致其他更糟糕的误差情况出现。然而,如果使用浮点数的方式,则
- 内存中 : 0 1001 0101 0000 0000 0000 0000 0000 000
- 二进制范围 :1000 0000 0000 0000 0000 000.0000 0000 … ~ 1000 0000 0000 0000 0000 000.0111 1111 …
- 十进制范围 : 4194304.0 ~ 4194304.499…
- 内存中 : 0 1001 0101 0000 0000 0000 0000 0000 001
- 二进制范围 :1000 0000 0000 0000 0000 000.1000 0000 … ~ 1000 0000 0000 0000 0000 000.1111 1111 …
- 十进制范围 : 4194304.5 ~ 4194304.999…
- 因此,对于单精度浮点数来说,有效数字最大能表示 2 ^ (23 + 1) - 1 = 16777215 ,即只能保证 7 位有效数字,双精度浮点数最大能 2 ^ (52 + 1) - 1 = 9007199254740991 ,即能保证 15 位有效数字。
量化方式
- 浮点数量化的编码方式有:
- T :截断,即把输入值乘以缩放因子,截断结果的小数部分,得到整数值。
- R :四舍五入,即把输入值乘以缩放因子,对结果四舍五入,得到整数值。
- 解码方式有:
- L :左重建,即把编码后的整数值,除以缩放因子,得到浮点数值。
- C :中心重建,即把编码后的整数值,加上 0.5 后,再除以缩放因子,得到浮点数值。
TL
const int NSTEPS = 64;
int encoded = (int)(input * NSTEPS);
if (encoded > NSTEPS - 1)
{
encoded = NSTEPS - 1;
}
const float STEP_SIZE = (1.0f / NSTEPS);
float decoded = encoded * STEP_SIZE;
- 其中,NSTEPS 为缩放因子,input 为 [0 , 1] 区间的输入值,encoded 为编码后的值,decoded 为解码后的值。
- 示例数据如下:
| 输入值(input) |
编码值(encoded) |
解码值(decoded) |
偏差值 |
| 0.0 |
0 |
0.0 |
0.0 |
| 0.1 |
6 |
0.09375 |
-0.00625 |
| 0.2 |
12 |
0.1875 |
-0.0125 |
| 0.3 |
19 |
0.296875 |
-0.003125 |
| 0.4 |
25 |
0.390625 |
-0.009375 |
| 0.5 |
32 |
0.5 |
0 |
| 0.6 |
38 |
0.59375 |
-0.00625 |
| 0.7 |
44 |
0.6875 |
-0.0125 |
| 0.8 |
51 |
0.796875 |
-0.003125 |
| 0.9 |
57 |
0.890625 |
-0.009375 |
| 1.0 |
63 |
0.984375 |
-0.015625 |
- 从表中数据可以看到,对输入值执行 TL 过程的最终结果是将它们分流到原始值的左侧。然而,这种向左偏移在大多数应用场景中都是不好的,主要有两个原因:
- 结果通常会向 0 偏移,代表这个过程会偏向于能量损失。
- 最终浪费了存储空间(或带宽)。
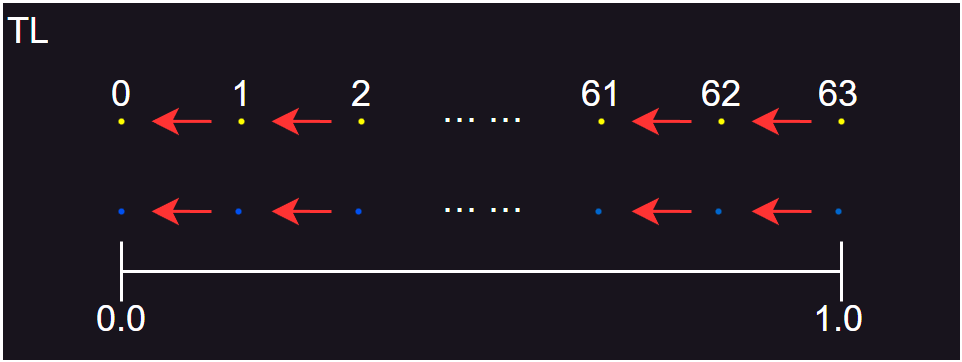
- TL 的量化图示如上图所示,其中白色点代表量化编码的整数结果值,蓝色点代表量化解码后的浮点数结果值,红色箭头表示两个相邻结果值之间的所有数的编码或解码映射方向。
TC
const int NSTEPS = 64;
int encoded = (int)(input * NSTEPS);
if (encoded > NSTEPS - 1)
{
encoded = NSTEPS - 1;
}
const float STEP_SIZE = (1.0f / NSTEPS);
float decoded = (encoded + 0.5f) * STEP_SIZE;
- 其中,NSTEPS 为缩放因子,input 为 [0 , 1] 区间的输入值,encoded 为编码后的值,decoded 为解码后的值。
- 示例数据如下:
| 输入值(input) |
编码值(encoded) |
解码值(decoded) |
偏差值 |
| 0.0 |
0 |
0.0078125 |
0.0078125 |
| 0.1 |
6 |
0.1015625 |
0.0015625 |
| 0.2 |
12 |
0.1953125 |
-0.0046875 |
| 0.3 |
19 |
0.3046875 |
0.0046875 |
| 0.4 |
25 |
0.3984375 |
-0.0015625 |
| 0.5 |
32 |
0.5078125 |
0.0078125 |
| 0.6 |
38 |
0.6015625 |
0.0015625 |
| 0.7 |
44 |
0.6953125 |
-0.0046875 |
| 0.8 |
51 |
0.8046875 |
0.0046875 |
| 0.9 |
57 |
0.8984375 |
-0.0015625 |
| 1.0 |
63 |
0.9921875 |
-0.0078125 |
- 可以看到,TC 会增大一部分输入值,也会减小一部分输入值,但如果对很多随机值进行编码,这些编码值解码后的平均值,会趋于输入值的平均值,即总能量基本不变。
- 然而,TC 有一个明显的问题,可能会比 TC 更糟糕,即无法表示 0 。也就是说,当输入值为 0 时,会得到一个很小的正数。如果用于表示速度,当对静止的对象的数据进行保存和加载时,静止的对象就变成在慢慢移动,会造成错误的结果。
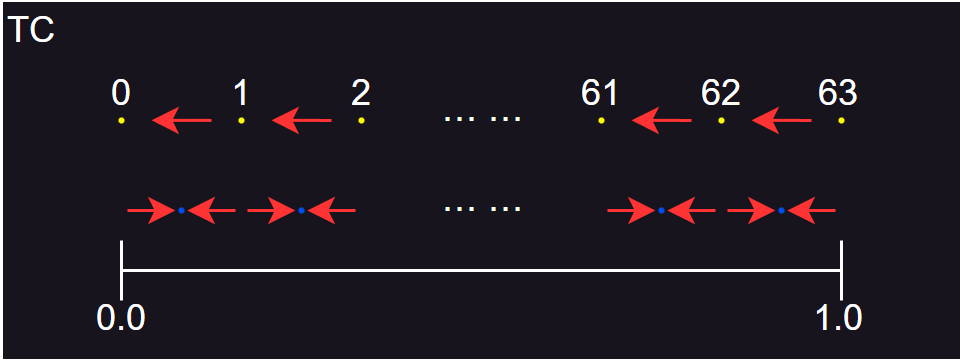
- TC 的量化图示如上图所示。
RL
const int NSTEPS = 64;
int encoded = (int)(input * (NSTEPS - 1) + 0.5f);
if (encoded > NSTEPS - 1)
{
encoded = NSTEPS - 1;
}
const float STEP_SIZE = (1.0f / (NSTEPS - 1));
float decoded = encoded * STEP_SIZE;
- 其中,NSTEPS - 1 为缩放因子,input 为 [0 , 1] 区间的输入值,encoded 为编码后的值,decoded 为解码后的值。
- 示例数据如下:
| 输入值(input) |
编码值(encoded) |
解码值(decoded) |
偏差值 |
| 0.0 |
0 |
0.0 |
0.0 |
| 0.1 |
6 |
0.09524 |
-0.00476 |
| 0.2 |
13 |
0.20635 |
0.00635 |
| 0.3 |
19 |
0.30159 |
0.00159 |
| 0.4 |
25 |
0.39683 |
-0.00317 |
| 0.5 |
32 |
0.50794 |
0.00794 |
| 0.6 |
38 |
0.60317 |
0.00317 |
| 0.7 |
44 |
0.69841 |
-0.00159 |
| 0.8 |
51 |
0.80952 |
0.00952 |
| 0.9 |
57 |
0.90476 |
0.00476 |
| 1.0 |
63 |
1.0 |
0.0 |
- RL 具有和 TC 一样的输出结果,但对应的输入值不一样。RL 可以表示 0 ,通过将缩放因子设置为 NSTEPS - 1 ,还可以表示 1 。
- 如果缩放因子仍为 NSTEPS ,接近 1 的值将得到比输入范围中的其他数字更向下映射,因此会引入比更多的错误,并且会出现能量减小的轻微趋势。
- 然而,为了达到与 TC 相同的误差目标,即整数代表的间隔相同,则 NSTEPS 需要加 1 ,使得带宽增大。如果 NSTEPS 很大,此时加 1 带来的额外代价很小,但如果 NSTEPS 很小,带宽增量就会比较明显,此时需要在 RL 和 TC 之间做选择。当不想考虑太多情况时,RL 是默认最安全、最稳定的方法。
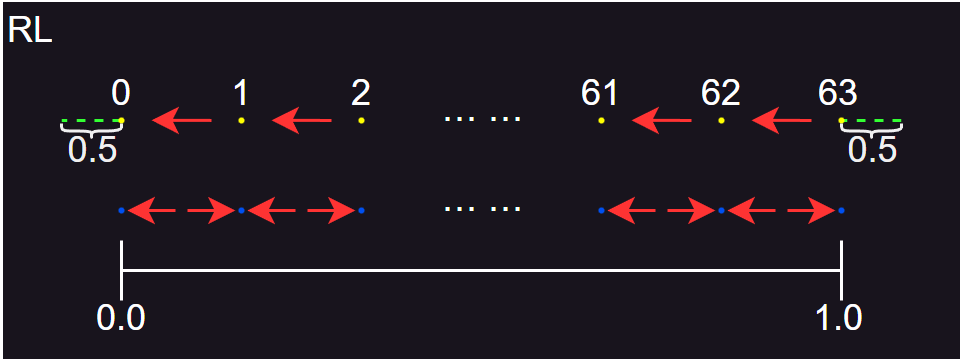
- RL 的量化图示如上图所示,其中虚线部分即为额外需要的 1 个区间范围。
RC
const int NSTEPS = 64;
int encoded = (int)(input * (NSTEPS - 1) + 0.5f);
if (encoded > NSTEPS - 1)
{
encoded = NSTEPS - 1;
}
const float STEP_SIZE = (1.0f / (NSTEPS - 1));
float decoded = (encoded + 0.5f) * STEP_SIZE;
- 其中,NSTEPS - 1 为缩放因子,input 为 [0 , 1] 区间的输入值,encoded 为编码后的值,decoded 为解码后的值。
- 示例数据如下:
| 输入值(input) |
编码值(encoded) |
解码值(decoded) |
偏差值 |
| 0.0 |
0 |
0.00794 |
0.00794 |
| 0.1 |
6 |
0.10317 |
0.00317 |
| 0.2 |
13 |
0.21429 |
0.01429 |
| 0.3 |
19 |
0.30952 |
0.00952 |
| 0.4 |
25 |
0.40476 |
0.00476 |
| 0.5 |
32 |
0.51587 |
0.01587 |
| 0.6 |
38 |
0.61111 |
0.01111 |
| 0.7 |
44 |
0.70635 |
0.00635 |
| 0.8 |
51 |
0.81746 |
0.01746 |
| 0.9 |
57 |
0.91270 |
0.01270 |
| 1.0 |
63 |
1.00794 |
0.00794 |
- 和 TL 类似,最终的结果都比输入值大,然而,这样的结果会比 TL 更加糟糕,因为会出现能量增加。能量损失能保证系统存在上限,而能量增加则往往会出现系统爆炸,所以通常不会考虑使用这种方式。
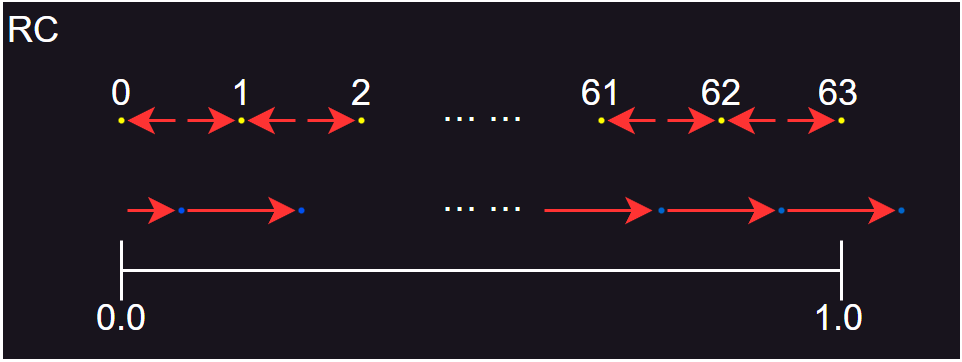
- RC 的量化图示如上图所示。
浮点数组合
- 整数量化中,通过减小整数的取值范围,可以将几个整数组合成一个整数值进行存储,使用时再根据每个数据使用的位进行解析。同样,浮点数也可以采用这种方式进行数据压缩。
- 对于两个浮点数,最容易考虑的方式,就是使用十进制的方式进行,即将浮点数放大,保留整数部分,将两个整数部分进行整合。然而,浮点数的有效数字位数只有 23 + 1 位,即每个浮点数编码后只能使用 12 位保留有效数字,当小数点后最多保留 3 位,对于 [0, 4] 区间内的值则能够进行表示。实现代码如下:
float a = 0.123f;
float b = 0.456f;
float c = 0.123 * 1000000 + 0.456 * 1000;
float a = Mathf.Floor(c / 1000) / 1000;
float b = Mathf.Floor(c % 1000) / 1000;
- 如果想要表示更大的范围,则需要使用二进制方式进行处理。前面提到,0.1 在内存中的表示为 0 0111 1011 1001 1001 1001 1001 1001 101 ,则
| 基础值 |
放大值 |
内存表示 |
| 0.1 |
2 ^ 0 |
0 0111 1011 1001 1001 1001 1001 1001 101 |
| 0.1 |
2 ^ 1 |
0 0111 1100 1001 1001 1001 1001 1001 101 |
| 0.1 |
2 ^ 10 |
0 1000 0101 1001 1001 1001 1001 1001 101 |
| 0.1 |
2 ^ 20 |
0 1000 1111 1001 1001 1001 1001 1001 101 |
- 可以看到,浮点数乘上 2 的次幂时,就是指数部分发生了变化,有效数字部分保持不变,因此在二进制下的处理方式为:
- 对输入值乘上 2 的次幂,进行放大,调整小数点的位置。
- 对浮点数进行取整,将小数点后的有效数字清 0 。
- 将一个浮点数乘上 2 ^ 12 ,进行移位操作,再与另一个浮点数相加,得到最终结果。
- 编码和解码的示例代码如下:
private float Encode(float x, float y)
{
double x0 = (int)(x * 512);
double y0 = (int)(y * 512);
return (float)((x0 * 4096) + y0);
}
private (float, float) Decode(float v)
{
float x = Mathf.Floor(v / 4096);
float y = v - 4096 * x;
float scale = 0.001953125f; // 1.0f / 512
return (x * scale, y * scale);
}
- 以 0.1 为例,编码过程如下:
- 进行放大后,在内存中为 0 1000 0100 1001 1001 1001 1001 1001 101 ,此时指数部分为 132 ,即小数点需要右移 132 - 127 = 5 位。
- 进行取整后,在内存中为 0 1000 0100 1001 1000 1000 0000 0000 000 ,此时有效数字部分为 1 1001 1000 1000 0000 0000 000 (首位 1 为浮点数省略表示的)。
- 进行移位后,在内存中为 0 1001 0000 1001 1000 1000 0000 0000 000 。
- 对两个浮点数进行相加,即对有效数字部分进行相加:
- 1 | 1001 1000 1000 0000 0000 000 | 0 0000 0000 000
- 0 | 0000 0000 0001 1001 1000 100 | 0 0000 0000 000
- 1 | 1001 1000 1001 1001 1000 100 | 0 0000 0000 000
- 最终结果为 0 1001 0000 1001 1000 1001 1001 1000 100 。
- 解码过程如下:
- 将编码值进行移位,得到 0 1000 0100 1001 1000 1001 1001 1000 100 ,此时指数部分为 132 ,即小数点需要右移 132 - 127 = 5 位。
- 向下取整,得到放大后的第一个浮点数,为 0 1000 0100 1001 1000 1000 0000 0000 000 。
- 计算另一个放大后的浮点数,指数部分为 1001 0000 ,即 144 ,同样使用有效数字部分进行相减:
- 1 | 1001 1000 1001 1001 1000 100
- 1 | 1001 1000 1000 0000 0000 000
- 0 | 0000 0000 0001 1001 1000 100
- 有效数字首位设置为 1 ,则指数部分为 144 - 12 = 132 ,因此另一个浮点数为 0 1000 0100 1001 1000 1000 0000 0000 000 。
- 将两个浮点数进行缩小,得到最终值,为 0 0111 1011 1001 1000 1000 0000 0000 000 ,即 0.0997314453125 。
- 从上面的过程可以看到,两个浮点数分别使用 12 个有效数字位。假设输入的浮点数,二进制下整数部分占 3 位,小数部分占 21 位,则按照编码过程放大 512 (2 ^ 9),则整数部分占 12 位,小数部分占 12 位,整数部分刚好能完全保留,第 13 ~ 24 位则全部置为 0 。而如果输入的浮点数整数部分占 4 位,则第 13 位不为 0 ,进行有效数字部分相加时,就会出现第一个浮点数的第 13 位的值加到第二个浮点数的第 1 位上,出现进位时,还会影响第一个浮点数的第 12 位,即两个浮点数的数据都受到影响,尤其是第二个浮点数,如:
- 1 | 1001 1000 1001 0000 0000 000 | 0 0000 0000 000
- 0 | 0000 0000 0001 1001 1000 100 | 1 0000 0000 000
- 1 | 1001 1000 1010 1001 1000 100 | 1 0000 0000 000
- 此时,两个有效数字为 1 1001 1000 101 和 0 1001 1000 100 ,可以看到第二个有效数字已经出现了很大的偏差,无法解码出正确的结果。
- 因此,编码过程的放大值,需要根据浮点数的大小进行调整。假设浮点数的整数部分最大值为 2 ^ n ,则放大值最大为 2 ^ (12 - n) ,其中 n <= 12 。需要注意,随着放大值减小,小数部分舍弃的有效值位数越多,则最终解码得到的值偏差会越来越大,需要根据具体使用环境选择合适的 n 值。
- 使用 RL 方式进行调整,则代码实现为:
private float Encode(float x, float y)
{
double x0 = (int)(x * 511);
double y0 = (int)(y * 511);
return (float)((x0 * 4096) + y0);
}
private (float, float) Decode(float v)
{
float x = Mathf.Floor(v / 4096);
float y = v - 4096 * x;
float scale = 1.0f / 511;
return (x * scale, y * scale);
}
参考








