Navmesh 的寻路依赖于导航网格的生成,本文将基于 Recast Navigation 源码进行分析。
简介
一、初始化生成配置
- 导航网格的生成配置结构
rcConfig如下:
// Recast/Include/Recast.h
...
struct rcConfig
{
/// The width of the field along the x-axis. [Limit: >= 0] [Units: vx]
int width;
/// The height of the field along the z-axis. [Limit: >= 0] [Units: vx]
int height;
/// The width/height size of tile's on the xz-plane. [Limit: >= 0] [Units: vx]
int tileSize;
/// The size of the non-navigable border around the heightfield. [Limit: >=0] [Units: vx]
int borderSize;
/// The xz-plane cell size to use for fields. [Limit: > 0] [Units: wu]
float cs;
/// The y-axis cell size to use for fields. [Limit: > 0] [Units: wu]
float ch;
/// The minimum bounds of the field's AABB. [(x, y, z)] [Units: wu]
float bmin[3];
/// The maximum bounds of the field's AABB. [(x, y, z)] [Units: wu]
float bmax[3];
/// The maximum slope that is considered walkable. [Limits: 0 <= value < 90] [Units: Degrees]
float walkableSlopeAngle;
/// Minimum floor to 'ceiling' height that will still allow the floor area to
/// be considered walkable. [Limit: >= 3] [Units: vx]
int walkableHeight;
/// Maximum ledge height that is considered to still be traversable. [Limit: >=0] [Units: vx]
int walkableClimb;
/// The distance to erode/shrink the walkable area of the heightfield away from
/// obstructions. [Limit: >=0] [Units: vx]
int walkableRadius;
/// The maximum allowed length for contour edges along the border of the mesh. [Limit: >=0] [Units: vx]
int maxEdgeLen;
/// The maximum distance a simplified contour's border edges should deviate
/// the original raw contour. [Limit: >=0] [Units: vx]
float maxSimplificationError;
/// The minimum number of cells allowed to form isolated island areas. [Limit: >=0] [Units: vx]
int minRegionArea;
/// Any regions with a span count smaller than this value will, if possible,
/// be merged with larger regions. [Limit: >=0] [Units: vx]
int mergeRegionArea;
/// The maximum number of vertices allowed for polygons generated during the
/// contour to polygon conversion process. [Limit: >= 3]
int maxVertsPerPoly;
/// Sets the sampling distance to use when generating the detail mesh.
/// (For height detail only.) [Limits: 0 or >= 0.9] [Units: wu]
float detailSampleDist;
/// The maximum distance the detail mesh surface should deviate from heightfield
/// data. (For height detail only.) [Limit: >=0] [Units: wu]
float detailSampleMaxError;
};
...
rcConfig参数的含义如下:width- 场在 x 轴上的宽度,由网格包围盒的宽度换算成单元格表示。
height- 场在 z 轴上的高度,由网格包围盒的高度换算成单元格表示。
tileSize- xz 平面上的瓦片大小。
borderSize- 高度场不可导航边界的大小。
cs- 场在 xz 平面上的单元格大小。
ch- 场在 y 轴上的单元格大小。
bmin[3]- 场的 AABB 包围盒的最小边界。
bmax[3]- 场的 AABB 包围盒的最大边界。
walkableSlopeAngle- 可行走的最大斜坡角度(0° ~ 90°)。
walkableHeight- 行走时地面到天花板的最小格子距离(>= 3)。
walkableClimb- 可跨越的最大格子高度。
walkableRadius- 在生成可行走区域时,需要从障碍物边缘向内收缩(侵蚀)的格子距离。
maxEdgeLen- 轮廓边缘在网格边界上的最大长度。
maxSimplificationError- 简化后的轮廓边缘和原轮廓之间需要偏离的最大距离。
minRegionArea- 形成孤岛区域的最小单元格数量。
mergeRegionArea- 区域包含的单元格数量少于该值时,尝试将此区域合并到更大的相邻区域。
maxVertsPerPoly- 单个多边形的最大顶点数(>= 3)。
detailSampleDist- 生成细节网格(高度细节)的采样间距(0 或 >= 0.9)。
detailSampleMaxError- 细节网格(高度细节)表面与原始高度场数据的最大允许偏差。
二、光栅化输入的多边形汤
- 输入的原始 3D 模型数据,通常是一组无序的三角形(或其他多边形),没有明确的拓扑结构或层级关系,这些多边形可能重叠、重复或不封闭,统称为多边形汤,光栅化过程需要对这一组三角形做处理。
创建高度场
- 高度场的结构如下:
// 高度场
struct rcHeightfield
{
...
int width; /// 高度场的宽度(沿 x 轴的单元格数量)
int height; /// 高度场的宽度(沿 z 轴的单元格数量)
float bmin[3]; /// 高度场在世界空间中的最小边界。 [(x, y, z)]
float bmax[3]; /// 高度场在世界空间中的最大边界。 [(x, y, z)]
float cs; /// 每个单元格的大小(在 xz 平面上)
float ch; /// 每个单元格的高度(沿 y 轴的最小增量)
rcSpan** spans; /// 高度场的跨度列表,列表包括所有单元格,每个单元格为一个跨度链表
rcSpanPool* pools; /// 跨度链表对象池
rcSpan* freelist; /// 跨度链表对象池的可用跨度对象列表
...
};
struct rcSpan
{
unsigned int smin : RC_SPAN_HEIGHT_BITS; /// 跨度的最小值,smin < smax
unsigned int smax : RC_SPAN_HEIGHT_BITS; /// 跨度的最大值,smax <= RC_SPAN_MAX_HEIGHT
unsigned int area : 6; /// 跨度所属区域 id
rcSpan* next; /// 下一个更高的跨度
};
- 通过
rcCreateHeightfield方法创建并初始化高度场,其实现如下:
// Recast/Source/Recast.cpp
...
bool rcCreateHeightfield(rcContext* context, rcHeightfield& heightfield, int sizeX, int sizeZ,
const float* minBounds, const float* maxBounds,
float cellSize, float cellHeight)
{
rcIgnoreUnused(context);
heightfield.width = sizeX;
heightfield.height = sizeZ;
rcVcopy(heightfield.bmin, minBounds);
rcVcopy(heightfield.bmax, maxBounds);
heightfield.cs = cellSize;
heightfield.ch = cellHeight;
heightfield.spans = (rcSpan**)rcAlloc(sizeof(rcSpan*) * heightfield.width * heightfield.height, RC_ALLOC_PERM);
if (!heightfield.spans)
{
return false;
}
memset(heightfield.spans, 0, sizeof(rcSpan*) * heightfield.width * heightfield.height);
return true;
}
...
- 高度场的初始化,即将
rcConfig的数据设置到高度场上。其中,spans为高度场的跨度数组,每个元素指向一个span链表,代表一个单元格cell上的所有跨度,数组长度为width * height。
标记可行走三角面
- 通过
rcMarkWalkableTriangles方法,将坡度小于walkableSlopeAngle的三角面标记为可行走区域,其实现如下:
// Recast/Source/Recast.cpp
...
void rcMarkWalkableTriangles(rcContext* context, const float walkableSlopeAngle,
const float* verts, const int numVerts,
const int* tris, const int numTris,
unsigned char* triAreaIDs)
{
rcIgnoreUnused(context);
rcIgnoreUnused(numVerts);
const float walkableThr = cosf(walkableSlopeAngle / 180.0f * RC_PI);
float norm[3];
for (int i = 0; i < numTris; ++i)
{
const int* tri = &tris[i * 3];
calcTriNormal(&verts[tri[0] * 3], &verts[tri[1] * 3], &verts[tri[2] * 3], norm);
// Check if the face is walkable.
if (norm[1] > walkableThr)
{
triAreaIDs[i] = RC_WALKABLE_AREA;
}
}
}
...
- 其中,
calcTriNormal方法用于计算三角面的归一化法线。三角面和法线的示意图如下: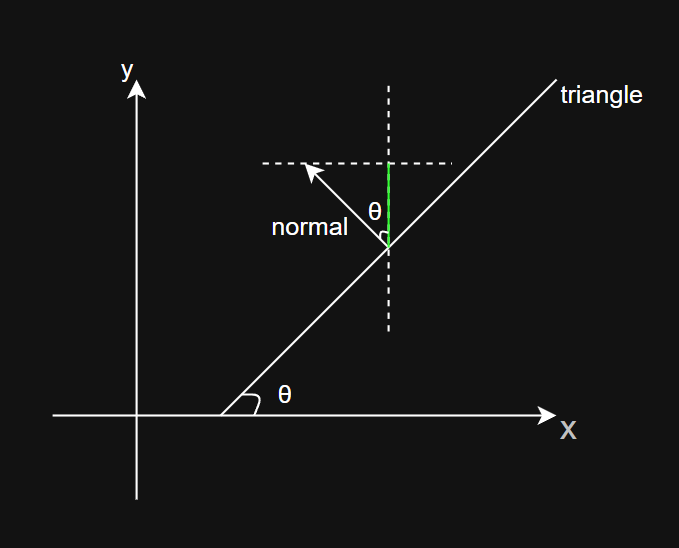
- 三角面和 xz 平面的夹角即为坡度 θ,而法线和 y 轴的夹角也为 θ。由于法线为归一化,则法线在 y 轴上的投影即为
cosθ。随着坡度 θ 增大,cosθ逐渐减小,当坡度 θ 小于walkableSlopeAngle时,该三角面则为可行走区域,将三角面的areaID设置为RC_WALKABLE_AREA。 - 光栅化前先对坡度较大的三角面进行过滤,比起光栅化后再对每一个
cell进行坡度判断,可以减少较多的计算量。
光栅化三角面
- 光栅化三角面的过程,主要是对每个三角面,通过
rasterizeTri方法进行处理,其实现如下:
// Recast/Source/RecastRasterization.cpp
static bool rasterizeTri(const float* v0, const float* v1, const float* v2,
const unsigned char areaID, rcHeightfield& heightfield,
const float* heightfieldBBMin, const float* heightfieldBBMax,
const float cellSize, const float inverseCellSize, const float inverseCellHeight,
const int flagMergeThreshold)
{
// Calculate the bounding box of the triangle.
float triBBMin[3];
rcVcopy(triBBMin, v0);
rcVmin(triBBMin, v1);
rcVmin(triBBMin, v2);
float triBBMax[3];
rcVcopy(triBBMax, v0);
rcVmax(triBBMax, v1);
rcVmax(triBBMax, v2);
// If the triangle does not touch the bounding box of the heightfield, skip the triangle.
if (!overlapBounds(triBBMin, triBBMax, heightfieldBBMin, heightfieldBBMax))
{
return true;
}
const int w = heightfield.width;
const int h = heightfield.height;
const float by = heightfieldBBMax[1] - heightfieldBBMin[1];
// Calculate the footprint of the triangle on the grid's z-axis
int z0 = (int)((triBBMin[2] - heightfieldBBMin[2]) * inverseCellSize);
int z1 = (int)((triBBMax[2] - heightfieldBBMin[2]) * inverseCellSize);
// use -1 rather than 0 to cut the polygon properly at the start of the tile
z0 = rcClamp(z0, -1, h - 1);
z1 = rcClamp(z1, 0, h - 1);
// Clip the triangle into all grid cells it touches.
float buf[7 * 3 * 4];
float* in = buf;
float* inRow = buf + 7 * 3;
float* p1 = inRow + 7 * 3;
float* p2 = p1 + 7 * 3;
rcVcopy(&in[0], v0);
rcVcopy(&in[1 * 3], v1);
rcVcopy(&in[2 * 3], v2);
int nvRow;
int nvIn = 3;
for (int z = z0; z <= z1; ++z)
{
// Clip polygon to row. Store the remaining polygon as well
const float cellZ = heightfieldBBMin[2] + (float)z * cellSize;
dividePoly(in, nvIn, inRow, &nvRow, p1, &nvIn, cellZ + cellSize, RC_AXIS_Z);
rcSwap(in, p1);
if (nvRow < 3)
{
continue;
}
if (z < 0)
{
continue;
}
// find X-axis bounds of the row
float minX = inRow[0];
float maxX = inRow[0];
for (int vert = 1; vert < nvRow; ++vert)
{
if (minX > inRow[vert * 3])
{
minX = inRow[vert * 3];
}
if (maxX < inRow[vert * 3])
{
maxX = inRow[vert * 3];
}
}
int x0 = (int)((minX - heightfieldBBMin[0]) * inverseCellSize);
int x1 = (int)((maxX - heightfieldBBMin[0]) * inverseCellSize);
if (x1 < 0 || x0 >= w)
{
continue;
}
x0 = rcClamp(x0, -1, w - 1);
x1 = rcClamp(x1, 0, w - 1);
int nv;
int nv2 = nvRow;
for (int x = x0; x <= x1; ++x)
{
// Clip polygon to column. store the remaining polygon as well
const float cx = heightfieldBBMin[0] + (float)x * cellSize;
dividePoly(inRow, nv2, p1, &nv, p2, &nv2, cx + cellSize, RC_AXIS_X);
rcSwap(inRow, p2);
if (nv < 3)
{
continue;
}
if (x < 0)
{
continue;
}
// Calculate min and max of the span.
float spanMin = p1[1];
float spanMax = p1[1];
for (int vert = 1; vert < nv; ++vert)
{
spanMin = rcMin(spanMin, p1[vert * 3 + 1]);
spanMax = rcMax(spanMax, p1[vert * 3 + 1]);
}
spanMin -= heightfieldBBMin[1];
spanMax -= heightfieldBBMin[1];
// Skip the span if it's completely outside the heightfield bounding box
if (spanMax < 0.0f)
{
continue;
}
if (spanMin > by)
{
continue;
}
// Clamp the span to the heightfield bounding box.
if (spanMin < 0.0f)
{
spanMin = 0;
}
if (spanMax > by)
{
spanMax = by;
}
// Snap the span to the heightfield height grid.
unsigned short spanMinCellIndex = (unsigned short)rcClamp((int)floorf(spanMin * inverseCellHeight), 0, RC_SPAN_MAX_HEIGHT);
unsigned short spanMaxCellIndex = (unsigned short)rcClamp((int)ceilf(spanMax * inverseCellHeight), (int)spanMinCellIndex + 1, RC_SPAN_MAX_HEIGHT);
if (!addSpan(heightfield, x, z, spanMinCellIndex, spanMaxCellIndex, areaID, flagMergeThreshold))
{
return false;
}
}
}
return true;
}
...
- 光栅化过程就是将三角面沿着 z 轴和 x 轴进行切分,再计算 y 高度,从而得到多个长方体,主要步骤如下:
- 计算三角面包围盒的最大最小值,检查包围盒是否和高度场的包围盒有交集,无交集则不需要处理。
- 将三角面包围盒的 z 坐标最大最小值,以高度场包围盒 z 坐标最小值为基准,转化为
cell的 z' 表示。 - 将 z' 最小值限制为 [-1, heightfield.height - 1] ,最大值限制为 [0, heightfield.height - 1] 。
- 遍历 z' 坐标最小值到最大值区间,通过
dividePoly方法,将三角面按cell的 z' 切分成多个多边形。 - 对每个切分后的多边形,计算包围盒的 x 坐标最大最小值,,以高度场包围盒 x 坐标最小值为基准,转化为
cell的 x' 表示。 - 将 x' 最小值限制为 [-1, heightfield.width - 1] , 最大值限制为 [0, heightfield.width - 1] 。
- 遍历 x' 坐标最小值到最大值区间,通过
dividePoly方法,将多边形按cell的 x' 坐标再切分成多个子多边形。 - 对每个子多边形,计算顶点的 y 坐标最大最小值,以高度场包围盒 y 坐标最小值为基准。
- 将顶点 y 坐标最大最小值,转换成
cell的索引 ymax' 、ymin' 表示,最小值为 [0,RC_SPAN_MAX_HEIGHT] ,最大值为 [最小值 + 1,RC_SPAN_MAX_HEIGHT] 。 - 调用
addSpan方法,将当前 x' 、z' 对应的cell的 ymax' 、ymin' 索引区间,加入到高度场中。
- 分割多边形方法
dividePoly的实现如下:
// Recast/Source/RecastRasterization.cpp
static void dividePoly(const float* inVerts, int inVertsCount,
float* outVerts1, int* outVerts1Count,
float* outVerts2, int* outVerts2Count,
float axisOffset, rcAxis axis)
{
rcAssert(inVertsCount <= 12);
// How far positive or negative away from the separating axis is each vertex.
float inVertAxisDelta[12];
for (int inVert = 0; inVert < inVertsCount; ++inVert)
{
inVertAxisDelta[inVert] = axisOffset - inVerts[inVert * 3 + axis];
}
int poly1Vert = 0;
int poly2Vert = 0;
for (int inVertA = 0, inVertB = inVertsCount - 1; inVertA < inVertsCount; inVertB = inVertA, ++inVertA)
{
// If the two vertices are on the same side of the separating axis
bool sameSide = (inVertAxisDelta[inVertA] >= 0) == (inVertAxisDelta[inVertB] >= 0);
if (!sameSide)
{
float s = inVertAxisDelta[inVertB] / (inVertAxisDelta[inVertB] - inVertAxisDelta[inVertA]);
outVerts1[poly1Vert * 3 + 0] = inVerts[inVertB * 3 + 0] + (inVerts[inVertA * 3 + 0] - inVerts[inVertB * 3 + 0]) * s;
outVerts1[poly1Vert * 3 + 1] = inVerts[inVertB * 3 + 1] + (inVerts[inVertA * 3 + 1] - inVerts[inVertB * 3 + 1]) * s;
outVerts1[poly1Vert * 3 + 2] = inVerts[inVertB * 3 + 2] + (inVerts[inVertA * 3 + 2] - inVerts[inVertB * 3 + 2]) * s;
rcVcopy(&outVerts2[poly2Vert * 3], &outVerts1[poly1Vert * 3]);
poly1Vert++;
poly2Vert++;
// add the inVertA point to the right polygon. Do NOT add points that are on the dividing line
// since these were already added above
if (inVertAxisDelta[inVertA] > 0)
{
rcVcopy(&outVerts1[poly1Vert * 3], &inVerts[inVertA * 3]);
poly1Vert++;
}
else if (inVertAxisDelta[inVertA] < 0)
{
rcVcopy(&outVerts2[poly2Vert * 3], &inVerts[inVertA * 3]);
poly2Vert++;
}
}
else
{
// add the inVertA point to the right polygon. Addition is done even for points on the dividing line
if (inVertAxisDelta[inVertA] >= 0)
{
rcVcopy(&outVerts1[poly1Vert * 3], &inVerts[inVertA * 3]);
poly1Vert++;
if (inVertAxisDelta[inVertA] != 0)
{
continue;
}
}
rcVcopy(&outVerts2[poly2Vert * 3], &inVerts[inVertA * 3]);
poly2Vert++;
}
}
*outVerts1Count = poly1Vert;
*outVerts2Count = poly2Vert;
}
...
- 分割多边形的主要步骤为:
- 沿指定轴
axis方向,计算分割面和每个顶点的的指定轴坐标差值,用于确定顶点是否在分割面以内。 - 遍历每一个顶点,根据当前顶点 A 和上一个顶点 B所处位置进行处理。
- 如果 A 、B 处在分割面两侧:
- 计算 B 点到分割面的距离占 AB 到分割面距离和的比例。
- 根据比例,通过 A 、B 的坐标插值得到 AB 和分割面的交点 C 坐标。
- 将 C 点加入到分割面内顶点列表
outVerts1和分割面外顶点列表outVerts2中。 - 根据 A 点和分割面的位置关系,将 A 点加入到对应顶点列表中。
- 如果 A 、B 处在分割面内侧,将 A 点加入到分割面内顶点列表
outVerts1。 - 如果 A 、B 处在分割面外侧,将 A 点加入到分割面外顶点列表
outVerts2。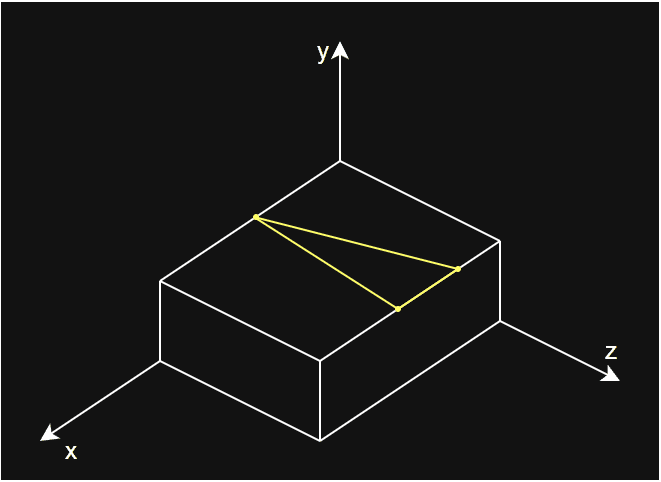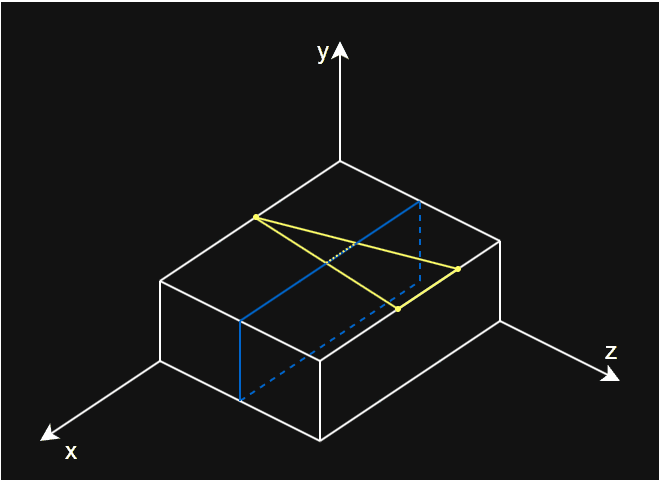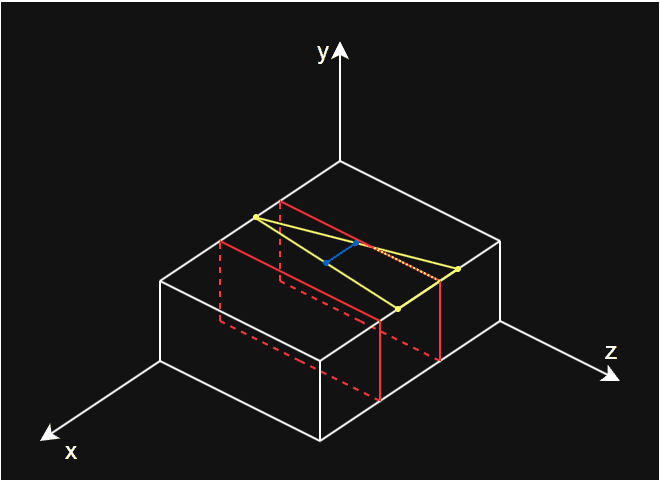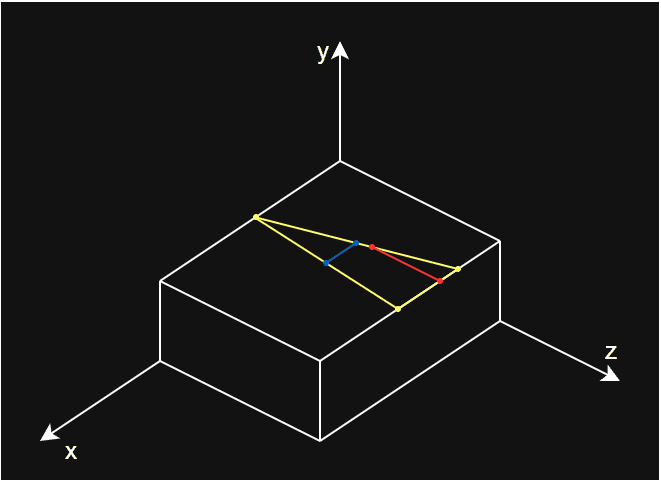
- 如果 A 、B 处在分割面两侧:
- 沿指定轴
- 高度场添加
span信息addSpan方法的实现如下:
// Recast/Source/RecastRasterization.cpp
...
static bool addSpan(rcHeightfield& heightfield,
const int x, const int z,
const unsigned short min, const unsigned short max,
const unsigned char areaID, const int flagMergeThreshold)
{
// Create the new span.
rcSpan* newSpan = allocSpan(heightfield);
if (newSpan == NULL)
{
return false;
}
newSpan->smin = min;
newSpan->smax = max;
newSpan->area = areaID;
newSpan->next = NULL;
const int columnIndex = x + z * heightfield.width;
rcSpan* previousSpan = NULL;
rcSpan* currentSpan = heightfield.spans[columnIndex];
// Insert the new span, possibly merging it with existing spans.
while (currentSpan != NULL)
{
if (currentSpan->smin > newSpan->smax)
{
// Current span is completely after the new span, break.
break;
}
if (currentSpan->smax < newSpan->smin)
{
// Current span is completely before the new span. Keep going.
previousSpan = currentSpan;
currentSpan = currentSpan->next;
}
else
{
// The new span overlaps with an existing span. Merge them.
if (currentSpan->smin < newSpan->smin)
{
newSpan->smin = currentSpan->smin;
}
if (currentSpan->smax > newSpan->smax)
{
newSpan->smax = currentSpan->smax;
}
// Merge flags.
if (rcAbs((int)newSpan->smax - (int)currentSpan->smax) <= flagMergeThreshold)
{
// Higher area ID numbers indicate higher resolution priority.
newSpan->area = rcMax(newSpan->area, currentSpan->area);
}
// Remove the current span since it's now merged with newSpan.
// Keep going because there might be other overlapping spans that also need to be merged.
rcSpan* next = currentSpan->next;
freeSpan(heightfield, currentSpan);
if (previousSpan)
{
previousSpan->next = next;
}
else
{
heightfield.spans[columnIndex] = next;
}
currentSpan = next;
}
}
// Insert new span after prev
if (previousSpan != NULL)
{
newSpan->next = previousSpan->next;
previousSpan->next = newSpan;
}
else
{
// This span should go before the others in the list
newSpan->next = heightfield.spans[columnIndex];
heightfield.spans[columnIndex] = newSpan;
}
return true;
}
...
span为一个跨度区间,包含 ymax' 、ymin'。在高度场中,span信息通过链表存储,记录了每一个cell的所有span区间,区间按坐标从小到大顺序存储。插入新区间时,同样需要保持从小到大的顺序,找到插入位置。如果新区间和原有区间有相交,则会将两个区间进行合并。
三、过滤可行走表面
- 在三角面上行走,需要满足几个主要情况:
- 三角面的坡度较平缓,过于陡峭的坡度无法行走。
- 相邻三角面高度差较低,支持对象跨越。
- 相邻三角面的天花板和地面之间的最小距离足够大,支持对象通过。
- 坡度的过滤在光栅化过程已经完成,此阶段不需要再处理。另外两个条件,通过三个过滤方式来处理。
处理低悬挂障碍物
- 通过
rcFilterLowHangingWalkableObstacles方法,进行低悬挂障碍物的处理,其实现如下:
// Recast/Source/RecastFilter.cpp
...
void rcFilterLowHangingWalkableObstacles(rcContext* context, const int walkableClimb, rcHeightfield& heightfield)
{
rcAssert(context);
rcScopedTimer timer(context, RC_TIMER_FILTER_LOW_OBSTACLES);
const int xSize = heightfield.width;
const int zSize = heightfield.height;
for (int z = 0; z < zSize; ++z)
{
for (int x = 0; x < xSize; ++x)
{
rcSpan* previousSpan = NULL;
bool previousWasWalkable = false;
unsigned char previousAreaID = RC_NULL_AREA;
// For each span in the column...
for (rcSpan* span = heightfield.spans[x + z * xSize]; span != NULL; previousSpan = span, span = span->next)
{
const bool walkable = span->area != RC_NULL_AREA;
// If current span is not walkable, but there is walkable span just below it and the height difference
// is small enough for the agent to walk over, mark the current span as walkable too.
if (!walkable && previousWasWalkable && (int)span->smax - (int)previousSpan->smax <= walkableClimb)
{
span->area = previousAreaID;
}
// Copy the original walkable value regardless of whether we changed it.
// This prevents multiple consecutive non-walkable spans from being erroneously marked as walkable.
previousWasWalkable = walkable;
previousAreaID = span->area;
}
}
}
}
...
- 检查 xz 平面的每个
cell的span列表,span列表是从小到大排序的,当前span不可行走时,如果上一个span可行走,且当前span的地面span->max和上一个span的地面previousSpan->max的差不超过可跨域距离walkableClimb,则将当前span->area标记为可行走区域。 - 加入此检查,可以避免角色因低障碍物(如:门槛、小台阶等)而受到阻挡无法行走,以及对于一些悬挂的障碍(如:桥梁、屋檐)等,可以支持角色跨越通过。
处理边缘跨度
- 处理边缘
span的方法rcFilterLedgeSpans如下:
// Recast/Source/RecastFilter.cpp
...
void rcFilterLedgeSpans(rcContext* context, const int walkableHeight, const int walkableClimb, rcHeightfield& heightfield)
{
rcAssert(context);
rcScopedTimer timer(context, RC_TIMER_FILTER_BORDER);
const int xSize = heightfield.width;
const int zSize = heightfield.height;
// Mark spans that are adjacent to a ledge as unwalkable..
for (int z = 0; z < zSize; ++z)
{
for (int x = 0; x < xSize; ++x)
{
for (rcSpan* span = heightfield.spans[x + z * xSize]; span; span = span->next)
{
// Skip non-walkable spans.
if (span->area == RC_NULL_AREA)
{
continue;
}
const int floor = (int)(span->smax);
const int ceiling = span->next ? (int)(span->next->smin) : MAX_HEIGHTFIELD_HEIGHT;
// The difference between this walkable area and the lowest neighbor walkable area.
// This is the difference between the current span and all neighbor spans that have
// enough space for an agent to move between, but not accounting at all for surface slope.
int lowestNeighborFloorDifference = MAX_HEIGHTFIELD_HEIGHT;
// Min and max height of accessible neighbours.
int lowestTraversableNeighborFloor = span->smax;
int highestTraversableNeighborFloor = span->smax;
for (int direction = 0; direction < 4; ++direction)
{
const int neighborX = x + rcGetDirOffsetX(direction);
const int neighborZ = z + rcGetDirOffsetY(direction);
// Skip neighbours which are out of bounds.
if (neighborX < 0 || neighborZ < 0 || neighborX >= xSize || neighborZ >= zSize)
{
lowestNeighborFloorDifference = -walkableClimb - 1;
break;
}
const rcSpan* neighborSpan = heightfield.spans[neighborX + neighborZ * xSize];
// The most we can step down to the neighbor is the walkableClimb distance.
// Start with the area under the neighbor span
int neighborCeiling = neighborSpan ? (int)neighborSpan->smin : MAX_HEIGHTFIELD_HEIGHT;
// Skip neighbour if the gap between the spans is too small.
if (rcMin(ceiling, neighborCeiling) - floor >= walkableHeight)
{
lowestNeighborFloorDifference = (-walkableClimb - 1);
break;
}
// For each span in the neighboring column...
for (; neighborSpan != NULL; neighborSpan = neighborSpan->next)
{
const int neighborFloor = (int)neighborSpan->smax;
neighborCeiling = neighborSpan->next ? (int)neighborSpan->next->smin : MAX_HEIGHTFIELD_HEIGHT;
// Only consider neighboring areas that have enough overlap to be potentially traversable.
if (rcMin(ceiling, neighborCeiling) - rcMax(floor, neighborFloor) < walkableHeight)
{
// No space to traverse between them.
continue;
}
const int neighborFloorDifference = neighborFloor - floor;
lowestNeighborFloorDifference = rcMin(lowestNeighborFloorDifference, neighborFloorDifference);
// Find min/max accessible neighbor height.
// Only consider neighbors that are at most walkableClimb away.
if (rcAbs(neighborFloorDifference) <= walkableClimb)
{
// There is space to move to the neighbor cell and the slope isn't too much.
lowestTraversableNeighborFloor = rcMin(lowestTraversableNeighborFloor, neighborFloor);
highestTraversableNeighborFloor = rcMax(highestTraversableNeighborFloor, neighborFloor);
}
else if (neighborFloorDifference < -walkableClimb)
{
// We already know this will be considered a ledge span so we can early-out
break;
}
}
}
// The current span is close to a ledge if the magnitude of the drop to any neighbour span is greater than the walkableClimb distance.
// That is, there is a gap that is large enough to let an agent move between them, but the drop (surface slope) is too large to allow it.
// (If this is the case, then biggestNeighborStepDown will be negative, so compare against the negative walkableClimb as a means of checking
// the magnitude of the delta)
if (lowestNeighborFloorDifference < -walkableClimb)
{
span->area = RC_NULL_AREA;
}
// If the difference between all neighbor floors is too large, this is a steep slope, so mark the span as an unwalkable ledge.
else if (highestTraversableNeighborFloor - lowestTraversableNeighborFloor > walkableClimb)
{
span->area = RC_NULL_AREA;
}
}
}
}
}
...
- 和低障碍处理类似,需要对 xz 平面上,每一个
cell的span列表heightfield.spans中的每一个span进行处理,处理流程大致如下:- 下一个跨度的天花板
span->next->smin和任一邻居跨度列表中的首个跨度天花板neightborSpan->smin,二者中的较小值,和当前跨度的地面span->smax的差值,不小于walkableHeight时,表示当前跨度和某个邻居存在较大的高度差,尽管可能只有一个方向存在危险,处于安全考虑,将当前跨度标记为不可行走,避免因局部地形问题卡住。 - 检查当前跨度和邻居跨度列表的每个跨度,当两者交集不小于
walkableHeight且地面高度差不大于walkableClimb时,认为此邻居跨度为可行走跨度,从所有可行走邻居跨度中,找出最大和最小的地面高度。 - 如果最大最小地面高度差超过
walkableClimb,则认为当前跨度为一个陡坡,将其span->area标记为不可行走。
- 下一个跨度的天花板
- 处理边缘
span采用保守策略,对于高度差较大的span,都选择标记为不可行走,减少特殊地形带来的角色移动表现问题的出现。
处理低高度跨度
- 低高度
span处理,主要是为了确保对象有足够空间可以在表面站立,才能够正常行走,通过rcFilterWalkableLowHeightSpans方法实现,代码如下:
// Recast/Source/RecastFilter.cpp
...
void rcFilterWalkableLowHeightSpans(rcContext* context, const int walkableHeight, rcHeightfield& heightfield)
{
rcAssert(context);
rcScopedTimer timer(context, RC_TIMER_FILTER_WALKABLE);
const int xSize = heightfield.width;
const int zSize = heightfield.height;
// Remove walkable flag from spans which do not have enough
// space above them for the agent to stand there.
for (int z = 0; z < zSize; ++z)
{
for (int x = 0; x < xSize; ++x)
{
for (rcSpan* span = heightfield.spans[x + z*xSize]; span; span = span->next)
{
const int floor = (int)(span->smax);
const int ceiling = span->next ? (int)(span->next->smin) : MAX_HEIGHTFIELD_HEIGHT;
if (ceiling - floor < walkableHeight)
{
span->area = RC_NULL_AREA;
}
}
}
}
}
- 低高度
span处理相对比较简单,就是对每一个span做检查,如果当前span的天花板(即下一个的最小值span->next->smin)和地面(span->smax)的高度差小于walkableHeight,即当前span不支持站立,则标记span->area为不可行走。
四、将可行走表面划分为地区
建立紧密高度场
- 经过上一步处理后,得到了一个高度场,但其中的
span使用链表存储,数据比较离散,不利于后续处理过程频繁访问,因此需要转换成更加紧凑的形式,即紧密高度场,其结构如下:
// 紧密高度场
struct rcCompactHeightfield
{
...
int width; /// 同 rcHeightfield::width
int height; /// 同 rcHeightfield::height
int spanCount; /// rcHeightfield 中的跨度总数
int walkableHeight; /// 同 rcConfig::walkableHeight
int walkableClimb; /// 同 rcConfig::walkableClimb
int borderSize; /// 同 rcConfig::borderSize
unsigned short maxDistance; /// 高度场中两个跨度的最大距离
unsigned short maxRegions; /// 高度场中的最大地区id
float bmin[3]; /// 同 rcHeightfield
float bmax[3]; /// 同 rcHeightfield
float cs; /// 同 rcHeightfield
float ch; /// 同 rcHeightfield
rcCompactCell* cells; /// 单元格数组,数量为 width * height
rcCompactSpan* spans; /// 跨度数组,数量为 spanCount
unsigned short* dist; /// 跨度和边界的距离数组,数量为 spanCount
unsigned char* areas; /// 区域id数组,数量为 spanCount
...
};
struct rcCompactCell
{
unsigned int index : 24; /// 当前单元格的首个跨度在的索引 id
unsigned int count : 8; /// 当前单元格的跨度数量
};
struct rcCompactSpan
{
unsigned short y; /// 当前跨度的地面高度,即 smax
unsigned short reg; /// 当前跨度所属的地区 id
unsigned int con : 24; /// 连通的邻居数据
unsigned int h : 8; /// 下一跨度的天花板到当前跨度的地面高度差,即 next->smin - smax
};
- 建立紧密高度场的方法
rcBuildCompactHeightfield如下:
// Recast/Source/Recast.cpp
...
bool rcBuildCompactHeightfield(rcContext* context, const int walkableHeight, const int walkableClimb,
const rcHeightfield& heightfield, rcCompactHeightfield& compactHeightfield)
{
...
const int MAX_HEIGHT = 0xffff;
// Fill in cells and spans.
int currentCellIndex = 0;
const int numColumns = xSize * zSize;
for (int columnIndex = 0; columnIndex < numColumns; ++columnIndex)
{
const rcSpan* span = heightfield.spans[columnIndex];
// If there are no spans at this cell, just leave the data to index=0, count=0.
if (span == NULL)
{
continue;
}
rcCompactCell& cell = compactHeightfield.cells[columnIndex];
cell.index = currentCellIndex;
cell.count = 0;
for (; span != NULL; span = span->next)
{
if (span->area != RC_NULL_AREA)
{
const int bot = (int)span->smax;
const int top = span->next ? (int)span->next->smin : MAX_HEIGHT;
compactHeightfield.spans[currentCellIndex].y = (unsigned short)rcClamp(bot, 0, 0xffff);
compactHeightfield.spans[currentCellIndex].h = (unsigned char)rcClamp(top - bot, 0, 0xff);
compactHeightfield.areas[currentCellIndex] = span->area;
currentCellIndex++;
cell.count++;
}
}
}
// Find neighbour connections.
const int MAX_LAYERS = RC_NOT_CONNECTED - 1;
int maxLayerIndex = 0;
const int zStride = xSize; // for readability
for (int z = 0; z < zSize; ++z)
{
for (int x = 0; x < xSize; ++x)
{
const rcCompactCell& cell = compactHeightfield.cells[x + z * zStride];
for (int i = (int)cell.index, ni = (int)(cell.index + cell.count); i < ni; ++i)
{
rcCompactSpan& span = compactHeightfield.spans[i];
for (int dir = 0; dir < 4; ++dir)
{
rcSetCon(span, dir, RC_NOT_CONNECTED);
const int neighborX = x + rcGetDirOffsetX(dir);
const int neighborZ = z + rcGetDirOffsetY(dir);
// First check that the neighbour cell is in bounds.
if (neighborX < 0 || neighborZ < 0 || neighborX >= xSize || neighborZ >= zSize)
{
continue;
}
// Iterate over all neighbour spans and check if any of the is
// accessible from current cell.
const rcCompactCell& neighborCell = compactHeightfield.cells[neighborX + neighborZ * zStride];
for (int k = (int)neighborCell.index, nk = (int)(neighborCell.index + neighborCell.count); k < nk; ++k)
{
const rcCompactSpan& neighborSpan = compactHeightfield.spans[k];
const int bot = rcMax(span.y, neighborSpan.y);
const int top = rcMin(span.y + span.h, neighborSpan.y + neighborSpan.h);
// Check that the gap between the spans is walkable,
// and that the climb height between the gaps is not too high.
if ((top - bot) >= walkableHeight && rcAbs((int)neighborSpan.y - (int)span.y) <= walkableClimb)
{
// Mark direction as walkable.
const int layerIndex = k - (int)neighborCell.index;
if (layerIndex < 0 || layerIndex > MAX_LAYERS)
{
maxLayerIndex = rcMax(maxLayerIndex, layerIndex);
continue;
}
rcSetCon(span, dir, layerIndex);
break;
}
}
}
}
}
}
if (maxLayerIndex > MAX_LAYERS)
{
context->log(RC_LOG_ERROR, "rcBuildCompactHeightfield: Heightfield has too many layers %d (max: %d)",
maxLayerIndex, MAX_LAYERS);
}
return true;
}
...
- 建立过程,每个
cell记录了其中首个span的索引及span的数量。所有cell的span都存入到compactHeightfield.spans中,其中y为当前span的地面高度span->smax,h为下一span的天花板到当前span地面的高度差span->next->smin - span->smax。 - 除了设置基础信息外,还需要计算每个
span的连通信息。每个span会和邻居cell的spans列表进行计算,当前span和邻居连通,需要满足以下条件:- 当前
span和邻居中的任意spans[index],两者的天花板高度y + h最小值和地面高度y最大值之差,不小于walkableHeight,即存在一个邻居span可以从当前span通行。 - 当前
span和邻居中的任意spans[index],两者的地面高度y之差,不大于walkableClimb,即存在一个邻居span可以从当前span跨过。
- 当前
- 设置连通的方法
rcSetCon的实现如下:
// Recast/Include/Recast.h
...
inline void rcSetCon(rcCompactSpan& span, int direction, int neighborIndex)
{
const unsigned int shift = (unsigned int)direction * 6;
const unsigned int con = span.con;
span.con = (con & ~(0x3f << shift)) | (((unsigned int)neighborIndex & 0x3f) << shift);
}
...
- 方向为左上右下,分别对应 0 ~ 3 ,每个方向使用一个 6 位的值,代表在邻居
cell中的第几个span,每个cell最多能有 62 个span。某个方向设置了连通后,则不再检查该方向后续的span,即取首个可连通的span。
收缩可行走区域
- 为了防止移动过程由于太靠近障碍边缘而出现问题,需要将可行走区域沿着障碍边缘进行收缩。收缩过程由
rcErodeWalkableArea方法实现,主要分为三个步骤:- 计算整个区域的边缘
span,其和边缘的距离distanceToBoundary[spanIndex]设置为 0。 - 计算每个非边缘
span和边缘的距离。 - 将距离小于阈值(
walkableRadius * 2)的compactHeightfield.areas[spanIndex]设置为不可通行。
- 计算整个区域的边缘
- 计算区域边缘的实现如下:
// Recast/Source/RecastArea.cpp
...
bool rcErodeWalkableArea(rcContext* context, const int erosionRadius, rcCompactHeightfield& compactHeightfield)
{
rcAssert(context != NULL);
const int xSize = compactHeightfield.width;
const int zSize = compactHeightfield.height;
const int& zStride = xSize; // For readability
rcScopedTimer timer(context, RC_TIMER_ERODE_AREA);
unsigned char* distanceToBoundary = (unsigned char*)rcAlloc(sizeof(unsigned char) * compactHeightfield.spanCount,
RC_ALLOC_TEMP);
if (!distanceToBoundary)
{
context->log(RC_LOG_ERROR, "erodeWalkableArea: Out of memory 'dist' (%d).", compactHeightfield.spanCount);
return false;
}
memset(distanceToBoundary, 0xff, sizeof(unsigned char) * compactHeightfield.spanCount);
// Mark boundary cells.
for (int z = 0; z < zSize; ++z)
{
for (int x = 0; x < xSize; ++x)
{
const rcCompactCell& cell = compactHeightfield.cells[x + z * zStride];
for (int spanIndex = (int)cell.index, maxSpanIndex = (int)(cell.index + cell.count); spanIndex < maxSpanIndex; ++spanIndex)
{
if (compactHeightfield.areas[spanIndex] == RC_NULL_AREA)
{
distanceToBoundary[spanIndex] = 0;
continue;
}
const rcCompactSpan& span = compactHeightfield.spans[spanIndex];
// Check that there is a non-null adjacent span in each of the 4 cardinal directions.
int neighborCount = 0;
for (int direction = 0; direction < 4; ++direction)
{
const int neighborConnection = rcGetCon(span, direction);
if (neighborConnection == RC_NOT_CONNECTED)
{
break;
}
const int neighborX = x + rcGetDirOffsetX(direction);
const int neighborZ = z + rcGetDirOffsetY(direction);
const int neighborSpanIndex = (int)compactHeightfield.cells[neighborX + neighborZ * zStride].index + neighborConnection;
if (compactHeightfield.areas[neighborSpanIndex] == RC_NULL_AREA)
{
break;
}
neighborCount++;
}
// At least one missing neighbour, so this is a boundary cell.
if (neighborCount != 4)
{
distanceToBoundary[spanIndex] = 0;
}
}
}
}
...
}
...
- 首先建立了
distanceToBoundary用于记录每个span和边缘的距离。其中不可行走的span(area为RC_NULL_AREA)即为边缘,将其distanceToBoundary[spanIndex]设为 0。检查四个邻居方向,如果有一个方向不可行走,则将该span也视为边缘,设置其距离为 0。 - 得到所有边缘数据后,就需要计算每个
span和边缘的距离,计算过程如下:
// Recast/Source/RecastArea.cpp
...
bool rcErodeWalkableArea(rcContext* context, const int erosionRadius, rcCompactHeightfield& compactHeightfield)
{
...
unsigned char newDistance;
// Pass 1
for (int z = 0; z < zSize; ++z)
{
for (int x = 0; x < xSize; ++x)
{
const rcCompactCell& cell = compactHeightfield.cells[x + z * zStride];
const int maxSpanIndex = (int)(cell.index + cell.count);
for (int spanIndex = (int)cell.index; spanIndex < maxSpanIndex; ++spanIndex)
{
const rcCompactSpan& span = compactHeightfield.spans[spanIndex];
if (rcGetCon(span, 0) != RC_NOT_CONNECTED)
{
// (-1,0)
const int aX = x + rcGetDirOffsetX(0);
const int aY = z + rcGetDirOffsetY(0);
const int aIndex = (int)compactHeightfield.cells[aX + aY * xSize].index + rcGetCon(span, 0);
const rcCompactSpan& aSpan = compactHeightfield.spans[aIndex];
newDistance = (unsigned char)rcMin((int)distanceToBoundary[aIndex] + 2, 255);
if (newDistance < distanceToBoundary[spanIndex])
{
distanceToBoundary[spanIndex] = newDistance;
}
// (-1,-1)
if (rcGetCon(aSpan, 3) != RC_NOT_CONNECTED)
{
const int bX = aX + rcGetDirOffsetX(3);
const int bY = aY + rcGetDirOffsetY(3);
const int bIndex = (int)compactHeightfield.cells[bX + bY * xSize].index + rcGetCon(aSpan, 3);
newDistance = (unsigned char)rcMin((int)distanceToBoundary[bIndex] + 3, 255);
if (newDistance < distanceToBoundary[spanIndex])
{
distanceToBoundary[spanIndex] = newDistance;
}
}
}
if (rcGetCon(span, 3) != RC_NOT_CONNECTED)
{
// (0,-1)
const int aX = x + rcGetDirOffsetX(3);
const int aY = z + rcGetDirOffsetY(3);
const int aIndex = (int)compactHeightfield.cells[aX + aY * xSize].index + rcGetCon(span, 3);
const rcCompactSpan& aSpan = compactHeightfield.spans[aIndex];
newDistance = (unsigned char)rcMin((int)distanceToBoundary[aIndex] + 2, 255);
if (newDistance < distanceToBoundary[spanIndex])
{
distanceToBoundary[spanIndex] = newDistance;
}
// (1,-1)
if (rcGetCon(aSpan, 2) != RC_NOT_CONNECTED)
{
const int bX = aX + rcGetDirOffsetX(2);
const int bY = aY + rcGetDirOffsetY(2);
const int bIndex = (int)compactHeightfield.cells[bX + bY * xSize].index + rcGetCon(aSpan, 2);
newDistance = (unsigned char)rcMin((int)distanceToBoundary[bIndex] + 3, 255);
if (newDistance < distanceToBoundary[spanIndex])
{
distanceToBoundary[spanIndex] = newDistance;
}
}
}
}
}
}
// Pass 2
for (int z = zSize - 1; z >= 0; --z)
{
for (int x = xSize - 1; x >= 0; --x)
{
const rcCompactCell& cell = compactHeightfield.cells[x + z * zStride];
const int maxSpanIndex = (int)(cell.index + cell.count);
for (int spanIndex = (int)cell.index; spanIndex < maxSpanIndex; ++spanIndex)
{
const rcCompactSpan& span = compactHeightfield.spans[spanIndex];
if (rcGetCon(span, 2) != RC_NOT_CONNECTED)
{
// (1,0)
const int aX = x + rcGetDirOffsetX(2);
const int aY = z + rcGetDirOffsetY(2);
const int aIndex = (int)compactHeightfield.cells[aX + aY * xSize].index + rcGetCon(span, 2);
const rcCompactSpan& aSpan = compactHeightfield.spans[aIndex];
newDistance = (unsigned char)rcMin((int)distanceToBoundary[aIndex] + 2, 255);
if (newDistance < distanceToBoundary[spanIndex])
{
distanceToBoundary[spanIndex] = newDistance;
}
// (1,1)
if (rcGetCon(aSpan, 1) != RC_NOT_CONNECTED)
{
const int bX = aX + rcGetDirOffsetX(1);
const int bY = aY + rcGetDirOffsetY(1);
const int bIndex = (int)compactHeightfield.cells[bX + bY * xSize].index + rcGetCon(aSpan, 1);
newDistance = (unsigned char)rcMin((int)distanceToBoundary[bIndex] + 3, 255);
if (newDistance < distanceToBoundary[spanIndex])
{
distanceToBoundary[spanIndex] = newDistance;
}
}
}
if (rcGetCon(span, 1) != RC_NOT_CONNECTED)
{
// (0,1)
const int aX = x + rcGetDirOffsetX(1);
const int aY = z + rcGetDirOffsetY(1);
const int aIndex = (int)compactHeightfield.cells[aX + aY * xSize].index + rcGetCon(span, 1);
const rcCompactSpan& aSpan = compactHeightfield.spans[aIndex];
newDistance = (unsigned char)rcMin((int)distanceToBoundary[aIndex] + 2, 255);
if (newDistance < distanceToBoundary[spanIndex])
{
distanceToBoundary[spanIndex] = newDistance;
}
// (-1,1)
if (rcGetCon(aSpan, 0) != RC_NOT_CONNECTED)
{
const int bX = aX + rcGetDirOffsetX(0);
const int bY = aY + rcGetDirOffsetY(0);
const int bIndex = (int)compactHeightfield.cells[bX + bY * xSize].index + rcGetCon(aSpan, 0);
newDistance = (unsigned char)rcMin((int)distanceToBoundary[bIndex] + 3, 255);
if (newDistance < distanceToBoundary[spanIndex])
{
distanceToBoundary[spanIndex] = newDistance;
}
}
}
}
}
}
...
}
...
- 计算
span到边缘的最小距离,最简单的做法就是计算其到每个边缘的距离,再从中取出最小值,显然效率非常低。这里使用了 8SSEDT 光栅扫描算法 来优化计算,做了两次扫描,这里按坐标原点在左下角计算,具体流程为:- 从下到上扫描,获取左、左下、下、右下邻居
span的距离,分别加上其到当前span的距离,取其中最小值作为当前span的距离。 - 从上到下扫描,获取右、右上、上、左上邻居
span的距离,分别加上其到当前span的距离,取其中最小值作为当前span的距离。
- 从下到上扫描,获取左、左下、下、右下邻居
- 其中,水平竖直方向的邻居和当前
span的距离设置为 2,对角线邻居和当前span的距离设置为 3,对角线邻居和水平竖直邻居的距离比为 1.5,接近 1.414,通过近似的结果来避免过程计算中出现频繁开根号的情况。扫描完成后,即可得到整个区域的距离场。 - 确定每个
span的距离后,即可通过比较距离和阈值的大小,来确定是否可通行,实现如下:
// Recast/Source/RecastArea.cpp
...
bool rcErodeWalkableArea(rcContext* context, const int erosionRadius, rcCompactHeightfield& compactHeightfield)
{
...
const unsigned char minBoundaryDistance = (unsigned char)(erosionRadius * 2);
for (int spanIndex = 0; spanIndex < compactHeightfield.spanCount; ++spanIndex)
{
if (distanceToBoundary[spanIndex] < minBoundaryDistance)
{
compactHeightfield.areas[spanIndex] = RC_NULL_AREA;
}
}
rcFree(distanceToBoundary);
return true;
}
...
- 为了尽可能远离边缘,使用两倍的
walkableRadius作为阈值划分,小于这个值的,该span的area都要标记为不可通行。
标记凸多边形区域
- 地图编辑过程,可能会预先对一些区域进行标记,如:不可通行、特殊区域(水池、草地等),此时则需要通过
rcMarkConvexPolyArea方法将这些区域更新到area中,其实现如下:
// Recast/Source/RecastArea.cpp
...
void rcMarkConvexPolyArea(rcContext* context, const float* verts, const int numVerts,
const float minY, const float maxY, unsigned char areaId,
rcCompactHeightfield& compactHeightfield)
{
rcAssert(context);
rcScopedTimer timer(context, RC_TIMER_MARK_CONVEXPOLY_AREA);
const int xSize = compactHeightfield.width;
const int zSize = compactHeightfield.height;
const int zStride = xSize; // For readability
// Compute the bounding box of the polygon
float bmin[3];
float bmax[3];
rcVcopy(bmin, verts);
rcVcopy(bmax, verts);
for (int i = 1; i < numVerts; ++i)
{
rcVmin(bmin, &verts[i * 3]);
rcVmax(bmax, &verts[i * 3]);
}
bmin[1] = minY;
bmax[1] = maxY;
// Compute the grid footprint of the polygon
int minx = (int)((bmin[0] - compactHeightfield.bmin[0]) / compactHeightfield.cs);
int miny = (int)((bmin[1] - compactHeightfield.bmin[1]) / compactHeightfield.ch);
int minz = (int)((bmin[2] - compactHeightfield.bmin[2]) / compactHeightfield.cs);
int maxx = (int)((bmax[0] - compactHeightfield.bmin[0]) / compactHeightfield.cs);
int maxy = (int)((bmax[1] - compactHeightfield.bmin[1]) / compactHeightfield.ch);
int maxz = (int)((bmax[2] - compactHeightfield.bmin[2]) / compactHeightfield.cs);
// Early-out if the polygon lies entirely outside the grid.
if (maxx < 0) { return; }
if (minx >= xSize) { return; }
if (maxz < 0) { return; }
if (minz >= zSize) { return; }
// Clamp the polygon footprint to the grid
if (minx < 0) { minx = 0; }
if (maxx >= xSize) { maxx = xSize - 1; }
if (minz < 0) { minz = 0; }
if (maxz >= zSize) { maxz = zSize - 1; }
// TODO: Optimize.
for (int z = minz; z <= maxz; ++z)
{
for (int x = minx; x <= maxx; ++x)
{
const rcCompactCell& cell = compactHeightfield.cells[x + z * zStride];
const int maxSpanIndex = (int)(cell.index + cell.count);
for (int spanIndex = (int)cell.index; spanIndex < maxSpanIndex; ++spanIndex)
{
rcCompactSpan& span = compactHeightfield.spans[spanIndex];
// Skip if span is removed.
if (compactHeightfield.areas[spanIndex] == RC_NULL_AREA)
{
continue;
}
// Skip if y extents don't overlap.
if ((int)span.y < miny || (int)span.y > maxy)
{
continue;
}
const float point[] = {
compactHeightfield.bmin[0] + ((float)x + 0.5f) * compactHeightfield.cs,
0,
compactHeightfield.bmin[2] + ((float)z + 0.5f) * compactHeightfield.cs
};
if (pointInPoly(numVerts, verts, point))
{
compactHeightfield.areas[spanIndex] = areaId;
}
}
}
}
}
...
- 根据多边形的顶点,计算出多边形的包围盒信息,找到紧密高度场中对应的
cell,遍历其中的span,找到可通行且和包围盒相交的span,计算其中心点在 xz 平面上的点。如果该点在多边形的投影面内,则表示该span属于当前的多边形,将其area设置为多边形的areaId。
建立地区
- 建立地区有几种算法:
- 分水岭划分(SAMPLE_PARTITION_WATERSHED)
- 单调划分(SAMPLE_PARTITION_MONOTONE)
- 分层划分(SAMPLE_PARTITION_LAYERS)
分水岭划分
- 分水岭划分算法,需要通过
rcBuildDistanceField先建立紧密高度场对应的高度场,包括两个步骤:calculateDistanceField计算高度场。boxBlur进行模糊处理。
calculateDistanceField的实现如下:
// Recast/Source/RecastRegion.cpp
...
static void calculateDistanceField(rcCompactHeightfield& chf, unsigned short* src, unsigned short& maxDist)
{
const int w = chf.width;
const int h = chf.height;
// Init distance and points.
for (int i = 0; i < chf.spanCount; ++i)
src[i] = 0xffff;
// Mark boundary cells.
for (int y = 0; y < h; ++y)
{
for (int x = 0; x < w; ++x)
{
const rcCompactCell& c = chf.cells[x+y*w];
for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i)
{
const rcCompactSpan& s = chf.spans[i];
const unsigned char area = chf.areas[i];
int nc = 0;
for (int dir = 0; dir < 4; ++dir)
{
if (rcGetCon(s, dir) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(dir);
const int ay = y + rcGetDirOffsetY(dir);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, dir);
if (area == chf.areas[ai])
nc++;
}
}
if (nc != 4)
src[i] = 0;
}
}
}
// Pass 1
for (int y = 0; y < h; ++y)
{
for (int x = 0; x < w; ++x)
{
const rcCompactCell& c = chf.cells[x+y*w];
for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i)
{
const rcCompactSpan& s = chf.spans[i];
if (rcGetCon(s, 0) != RC_NOT_CONNECTED)
{
// (-1,0)
const int ax = x + rcGetDirOffsetX(0);
const int ay = y + rcGetDirOffsetY(0);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, 0);
const rcCompactSpan& as = chf.spans[ai];
if (src[ai]+2 < src[i])
src[i] = src[ai]+2;
// (-1,-1)
if (rcGetCon(as, 3) != RC_NOT_CONNECTED)
{
const int aax = ax + rcGetDirOffsetX(3);
const int aay = ay + rcGetDirOffsetY(3);
const int aai = (int)chf.cells[aax+aay*w].index + rcGetCon(as, 3);
if (src[aai]+3 < src[i])
src[i] = src[aai]+3;
}
}
if (rcGetCon(s, 3) != RC_NOT_CONNECTED)
{
// (0,-1)
const int ax = x + rcGetDirOffsetX(3);
const int ay = y + rcGetDirOffsetY(3);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, 3);
const rcCompactSpan& as = chf.spans[ai];
if (src[ai]+2 < src[i])
src[i] = src[ai]+2;
// (1,-1)
if (rcGetCon(as, 2) != RC_NOT_CONNECTED)
{
const int aax = ax + rcGetDirOffsetX(2);
const int aay = ay + rcGetDirOffsetY(2);
const int aai = (int)chf.cells[aax+aay*w].index + rcGetCon(as, 2);
if (src[aai]+3 < src[i])
src[i] = src[aai]+3;
}
}
}
}
}
// Pass 2
for (int y = h-1; y >= 0; --y)
{
for (int x = w-1; x >= 0; --x)
{
const rcCompactCell& c = chf.cells[x+y*w];
for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i)
{
const rcCompactSpan& s = chf.spans[i];
if (rcGetCon(s, 2) != RC_NOT_CONNECTED)
{
// (1,0)
const int ax = x + rcGetDirOffsetX(2);
const int ay = y + rcGetDirOffsetY(2);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, 2);
const rcCompactSpan& as = chf.spans[ai];
if (src[ai]+2 < src[i])
src[i] = src[ai]+2;
// (1,1)
if (rcGetCon(as, 1) != RC_NOT_CONNECTED)
{
const int aax = ax + rcGetDirOffsetX(1);
const int aay = ay + rcGetDirOffsetY(1);
const int aai = (int)chf.cells[aax+aay*w].index + rcGetCon(as, 1);
if (src[aai]+3 < src[i])
src[i] = src[aai]+3;
}
}
if (rcGetCon(s, 1) != RC_NOT_CONNECTED)
{
// (0,1)
const int ax = x + rcGetDirOffsetX(1);
const int ay = y + rcGetDirOffsetY(1);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, 1);
const rcCompactSpan& as = chf.spans[ai];
if (src[ai]+2 < src[i])
src[i] = src[ai]+2;
// (-1,1)
if (rcGetCon(as, 0) != RC_NOT_CONNECTED)
{
const int aax = ax + rcGetDirOffsetX(0);
const int aay = ay + rcGetDirOffsetY(0);
const int aai = (int)chf.cells[aax+aay*w].index + rcGetCon(as, 0);
if (src[aai]+3 < src[i])
src[i] = src[aai]+3;
}
}
}
}
}
maxDist = 0;
for (int i = 0; i < chf.spanCount; ++i)
maxDist = rcMax(src[i], maxDist);
}
...
- 建立高度场的过程和
rcErodeWalkableArea的计算过程基本一致,rcErodeWalkableArea是将四个邻居中存在不可行走的span作为边缘,而calculateDistanceField则是再加上条件,如果四个邻居中存在和当前span的area不相同的,则认为是区域的边缘。得到边缘信息后,同样通过光栅扫描方式来计算距离,最终得到一个距离场。 boxBlur的实现如下:
// Recast/Source/RecastRegion.cpp
...
static unsigned short* boxBlur(rcCompactHeightfield& chf, int thr,
unsigned short* src, unsigned short* dst)
{
const int w = chf.width;
const int h = chf.height;
thr *= 2;
for (int y = 0; y < h; ++y)
{
for (int x = 0; x < w; ++x)
{
const rcCompactCell& c = chf.cells[x+y*w];
for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i)
{
const rcCompactSpan& s = chf.spans[i];
const unsigned short cd = src[i];
if (cd <= thr)
{
dst[i] = cd;
continue;
}
int d = (int)cd;
for (int dir = 0; dir < 4; ++dir)
{
if (rcGetCon(s, dir) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(dir);
const int ay = y + rcGetDirOffsetY(dir);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, dir);
d += (int)src[ai];
const rcCompactSpan& as = chf.spans[ai];
const int dir2 = (dir+1) & 0x3;
if (rcGetCon(as, dir2) != RC_NOT_CONNECTED)
{
const int ax2 = ax + rcGetDirOffsetX(dir2);
const int ay2 = ay + rcGetDirOffsetY(dir2);
const int ai2 = (int)chf.cells[ax2+ay2*w].index + rcGetCon(as, dir2);
d += (int)src[ai2];
}
else
{
d += cd;
}
}
else
{
d += cd*2;
}
}
dst[i] = (unsigned short)((d+5)/9);
}
}
}
return dst;
}
...
- 如果
span的距离不超过阈值thr(这里设置为 2),则不进行模糊计算,保持距离不变。如果超过,则需要以自身为中心,和周围八个邻居的距离进行平均,得到新的距离。其中,对于每个不可行走的邻居,使用中心的距离代替。 - 建立距离场后,就需要通过
rcBuildRegions划分地区,其实现如下:
// Recast/Source/RecastRegion.cpp
...
bool rcBuildRegions(rcContext* ctx, rcCompactHeightfield& chf,
const int borderSize, const int minRegionArea, const int mergeRegionArea)
{
rcAssert(ctx);
rcScopedTimer timer(ctx, RC_TIMER_BUILD_REGIONS);
const int w = chf.width;
const int h = chf.height;
rcScopedDelete<unsigned short> buf((unsigned short*)rcAlloc(sizeof(unsigned short)*chf.spanCount*2, RC_ALLOC_TEMP));
if (!buf)
{
ctx->log(RC_LOG_ERROR, "rcBuildRegions: Out of memory 'tmp' (%d).", chf.spanCount*4);
return false;
}
ctx->startTimer(RC_TIMER_BUILD_REGIONS_WATERSHED);
const int LOG_NB_STACKS = 3;
const int NB_STACKS = 1 << LOG_NB_STACKS;
rcTempVector<LevelStackEntry> lvlStacks[NB_STACKS];
for (int i=0; i<NB_STACKS; ++i)
lvlStacks[i].reserve(256);
rcTempVector<LevelStackEntry> stack;
stack.reserve(256);
unsigned short* srcReg = buf;
unsigned short* srcDist = buf+chf.spanCount;
memset(srcReg, 0, sizeof(unsigned short)*chf.spanCount);
memset(srcDist, 0, sizeof(unsigned short)*chf.spanCount);
unsigned short regionId = 1;
unsigned short level = (chf.maxDistance+1) & ~1;
// TODO: Figure better formula, expandIters defines how much the
// watershed "overflows" and simplifies the regions. Tying it to
// agent radius was usually good indication how greedy it could be.
// const int expandIters = 4 + walkableRadius * 2;
const int expandIters = 8;
if (borderSize > 0)
{
// Make sure border will not overflow.
const int bw = rcMin(w, borderSize);
const int bh = rcMin(h, borderSize);
// Paint regions
paintRectRegion(0, bw, 0, h, regionId|RC_BORDER_REG, chf, srcReg); regionId++;
paintRectRegion(w-bw, w, 0, h, regionId|RC_BORDER_REG, chf, srcReg); regionId++;
paintRectRegion(0, w, 0, bh, regionId|RC_BORDER_REG, chf, srcReg); regionId++;
paintRectRegion(0, w, h-bh, h, regionId|RC_BORDER_REG, chf, srcReg); regionId++;
}
chf.borderSize = borderSize;
int sId = -1;
while (level > 0)
{
level = level >= 2 ? level-2 : 0;
sId = (sId+1) & (NB_STACKS-1);
// ctx->startTimer(RC_TIMER_DIVIDE_TO_LEVELS);
if (sId == 0)
sortCellsByLevel(level, chf, srcReg, NB_STACKS, lvlStacks, 1);
else
appendStacks(lvlStacks[sId-1], lvlStacks[sId], srcReg); // copy left overs from last level
// ctx->stopTimer(RC_TIMER_DIVIDE_TO_LEVELS);
{
rcScopedTimer timerExpand(ctx, RC_TIMER_BUILD_REGIONS_EXPAND);
// Expand current regions until no empty connected cells found.
expandRegions(expandIters, level, chf, srcReg, srcDist, lvlStacks[sId], false);
}
{
rcScopedTimer timerFloor(ctx, RC_TIMER_BUILD_REGIONS_FLOOD);
// Mark new regions with IDs.
for (int j = 0; j<lvlStacks[sId].size(); j++)
{
LevelStackEntry current = lvlStacks[sId][j];
int x = current.x;
int y = current.y;
int i = current.index;
if (i >= 0 && srcReg[i] == 0)
{
if (floodRegion(x, y, i, level, regionId, chf, srcReg, srcDist, stack))
{
if (regionId == 0xFFFF)
{
ctx->log(RC_LOG_ERROR, "rcBuildRegions: Region ID overflow");
return false;
}
regionId++;
}
}
}
}
}
// Expand current regions until no empty connected cells found.
expandRegions(expandIters*8, 0, chf, srcReg, srcDist, stack, true);
ctx->stopTimer(RC_TIMER_BUILD_REGIONS_WATERSHED);
{
rcScopedTimer timerFilter(ctx, RC_TIMER_BUILD_REGIONS_FILTER);
// Merge regions and filter out small regions.
rcTempVector<int> overlaps;
chf.maxRegions = regionId;
if (!mergeAndFilterRegions(ctx, minRegionArea, mergeRegionArea, chf.maxRegions, chf, srcReg, overlaps))
return false;
// If overlapping regions were found during merging, split those regions.
if (overlaps.size() > 0)
{
ctx->log(RC_LOG_ERROR, "rcBuildRegions: %d overlapping regions.", overlaps.size());
}
}
// Write the result out.
for (int i = 0; i < chf.spanCount; ++i)
chf.spans[i].reg = srcReg[i];
return true;
}
...
rcBuildRegions的步骤如下:- 首先,根据边界尺寸
borderSize,通过paintRectRegion方法,将边界范围的region进行设置,并设置紧密高度场chf.borderSize为borderSize。 - 接着,设置
level为距离最大值向上取偶数,根据level的大小,从大到小,每次处理两级,处理流程如下:- 收集本次处理的所有
span到lvlStacks数组中。- 首次执行时,通过
sortCellsByLevel方法,检查所有span,将可行走且未设置region的,根据距离进行分段,放入lvlStacks[sId],sId越小,距离越远。第 0 段距离最小为level - 2向下取偶数,第 1 段为第 0 段的一半,以此类推,如:level为 7 ,则sId为 0,span距离不小于(7 - 2) / 2 * 2 / 2 ^ 0 = 4。sId为 1,span距离不小于(7 - 2) / 2 * 2 / 2 ^ 1 = 2。sId为 2,span距离不小于(7 - 2) / 2 * 2 / 2 ^ 2 = 1。
- 非首次执行,则通过
appendStacks方法,将上一次lvlStacks[sId-1]没有分配到region的,加入到lvlStacks[sId]中。
- 首次执行时,通过
- 通过
expandRegions方法,沿边界将当前region进行扩展。 - 遍历当前
lvlStacks[sId],通过floodRegion方法,填充span及其扩展的span的region,成功填充则regionId + 1。
- 收集本次处理的所有
- 调用
expandRegions方法,扩展所有未分配region的span。 - 调用
mergeAndFilterRegions方法,合并region,过滤掉region数量太小的span。 - 最后,将
srcReg记录的最终region信息,应用到紧密高度场中的每一个span,完成划分。
- 首先,根据边界尺寸
expandRegions的实现如下:
// Recast/Source/RecastRegion.cpp
...
static void expandRegions(int maxIter, unsigned short level,
rcCompactHeightfield& chf,
unsigned short* srcReg, unsigned short* srcDist,
rcTempVector<LevelStackEntry>& stack,
bool fillStack)
{
const int w = chf.width;
const int h = chf.height;
if (fillStack)
{
// Find cells revealed by the raised level.
stack.clear();
for (int y = 0; y < h; ++y)
{
for (int x = 0; x < w; ++x)
{
const rcCompactCell& c = chf.cells[x+y*w];
for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i)
{
if (chf.dist[i] >= level && srcReg[i] == 0 && chf.areas[i] != RC_NULL_AREA)
{
stack.push_back(LevelStackEntry(x, y, i));
}
}
}
}
}
else // use cells in the input stack
{
// mark all cells which already have a region
for (int j=0; j<stack.size(); j++)
{
int i = stack[j].index;
if (srcReg[i] != 0)
stack[j].index = -1;
}
}
rcTempVector<DirtyEntry> dirtyEntries;
int iter = 0;
while (stack.size() > 0)
{
int failed = 0;
dirtyEntries.clear();
for (int j = 0; j < stack.size(); j++)
{
int x = stack[j].x;
int y = stack[j].y;
int i = stack[j].index;
if (i < 0)
{
failed++;
continue;
}
unsigned short r = srcReg[i];
unsigned short d2 = 0xffff;
const unsigned char area = chf.areas[i];
const rcCompactSpan& s = chf.spans[i];
for (int dir = 0; dir < 4; ++dir)
{
if (rcGetCon(s, dir) == RC_NOT_CONNECTED) continue;
const int ax = x + rcGetDirOffsetX(dir);
const int ay = y + rcGetDirOffsetY(dir);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, dir);
if (chf.areas[ai] != area) continue;
if (srcReg[ai] > 0 && (srcReg[ai] & RC_BORDER_REG) == 0)
{
if ((int)srcDist[ai]+2 < (int)d2)
{
r = srcReg[ai];
d2 = srcDist[ai]+2;
}
}
}
if (r)
{
stack[j].index = -1; // mark as used
dirtyEntries.push_back(DirtyEntry(i, r, d2));
}
else
{
failed++;
}
}
// Copy entries that differ between src and dst to keep them in sync.
for (int i = 0; i < dirtyEntries.size(); i++) {
int idx = dirtyEntries[i].index;
srcReg[idx] = dirtyEntries[i].region;
srcDist[idx] = dirtyEntries[i].distance2;
}
if (failed == stack.size())
break;
if (level > 0)
{
++iter;
if (iter >= maxIter)
break;
}
}
}
...
expandRegions有两种处理模式:- 当
fillStack为true时,会清空stack,将所有不小于level、未分配region且可行走的span加入到stack中。 - 当
fillStack为false时,则使用已经收集好的stack,将其中已分配region的index设置为-1作为标记。
- 当
- 根据传入的
maxIter,决定进行循环迭代的次数,每次循环的处理流程为:- 遍历
stack中的span。- 如果
index为-1,则不再处理。 - 检查四个邻居中,可行走,已分配
region且不为边界(即不在borderSize范围)的span,找到其中距离最小的,将index、region、距离加入到dirtyEntries中,设置为stack[j].index = -1,即标记已处理。
- 如果
- 遍历
dirtyEntries,将其中的index对应的region和距离设置到srcReg和srcDist中。 - 进入下一次循环,直到
stack中没有未处理的span或者迭代次数达到上限。
- 遍历
floodRegion的实现如下:
// Recast/Source/RecastRegion.cpp
...
static bool floodRegion(int x, int y, int i,
unsigned short level, unsigned short r,
rcCompactHeightfield& chf,
unsigned short* srcReg, unsigned short* srcDist,
rcTempVector<LevelStackEntry>& stack)
{
const int w = chf.width;
const unsigned char area = chf.areas[i];
// Flood fill mark region.
stack.clear();
stack.push_back(LevelStackEntry(x, y, i));
srcReg[i] = r;
srcDist[i] = 0;
unsigned short lev = level >= 2 ? level-2 : 0;
int count = 0;
while (stack.size() > 0)
{
LevelStackEntry& back = stack.back();
int cx = back.x;
int cy = back.y;
int ci = back.index;
stack.pop_back();
const rcCompactSpan& cs = chf.spans[ci];
// Check if any of the neighbours already have a valid region set.
unsigned short ar = 0;
for (int dir = 0; dir < 4; ++dir)
{
// 8 connected
if (rcGetCon(cs, dir) != RC_NOT_CONNECTED)
{
const int ax = cx + rcGetDirOffsetX(dir);
const int ay = cy + rcGetDirOffsetY(dir);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(cs, dir);
if (chf.areas[ai] != area)
continue;
unsigned short nr = srcReg[ai];
if (nr & RC_BORDER_REG) // Do not take borders into account.
continue;
if (nr != 0 && nr != r)
{
ar = nr;
break;
}
const rcCompactSpan& as = chf.spans[ai];
const int dir2 = (dir+1) & 0x3;
if (rcGetCon(as, dir2) != RC_NOT_CONNECTED)
{
const int ax2 = ax + rcGetDirOffsetX(dir2);
const int ay2 = ay + rcGetDirOffsetY(dir2);
const int ai2 = (int)chf.cells[ax2+ay2*w].index + rcGetCon(as, dir2);
if (chf.areas[ai2] != area)
continue;
unsigned short nr2 = srcReg[ai2];
if (nr2 != 0 && nr2 != r)
{
ar = nr2;
break;
}
}
}
}
if (ar != 0)
{
srcReg[ci] = 0;
continue;
}
count++;
// Expand neighbours.
for (int dir = 0; dir < 4; ++dir)
{
if (rcGetCon(cs, dir) != RC_NOT_CONNECTED)
{
const int ax = cx + rcGetDirOffsetX(dir);
const int ay = cy + rcGetDirOffsetY(dir);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(cs, dir);
if (chf.areas[ai] != area)
continue;
if (chf.dist[ai] >= lev && srcReg[ai] == 0)
{
srcReg[ai] = r;
srcDist[ai] = 0;
stack.push_back(LevelStackEntry(ax, ay, ai));
}
}
}
}
return count > 0;
}
...
floodRegion每次从lvlStacks[sId]取一个index,处理其对应的span,放入stack中进行循环处理,流程如下:- 从
stack中取出一个span。 - 检查
span的八个邻居,如果没有分配过region或者region和传入的regionId相同,则将当前span的region设置为传入的regionId,距离设置为 0 。 - 如果当前
span设置了region,则将四个邻居中,可行走且大于level - 2,同时还未分配region的span,设置其region为regionId,距离设置为 0。 - 将处理的邻居
span放入stack中,循环处理stack,实现传播,直到stack处理完毕。
- 从
mergeAndFilterRegions使用了新的结构rcRegion来进行处理,其实现如下:
// Recast/Source/RecastRegion.cpp
...
struct rcRegion
{
...
int spanCount; // 当前地区的所有跨度的数量
unsigned short id; // 当前地区的 id
unsigned char areaType; // 当前地区的区域类型
bool remap; // 是否需要重新映射地区 id
bool visited; // 是否访问处理过
bool overlap; // 是否重叠,即在同一个单元格上存在多个相同地区的跨度
bool connectsToBorder; // 是否连接到 borderSize 范围内的边缘
unsigned short ymin, ymax;
rcTempVector<int> connections; // 地区的轮廓的地区 id 连接
rcTempVector<int> floors; // 和当前地区存在重叠(即处在同一个单元格)的所有其他地区 id
};
...
static bool mergeAndFilterRegions(rcContext* ctx, int minRegionArea, int mergeRegionSize,
unsigned short& maxRegionId,
rcCompactHeightfield& chf,
unsigned short* srcReg, rcTempVector<int>& overlaps)
{
const int w = chf.width;
const int h = chf.height;
const int nreg = maxRegionId+1;
rcTempVector<rcRegion> regions;
if (!regions.reserve(nreg)) {
ctx->log(RC_LOG_ERROR, "mergeAndFilterRegions: Out of memory 'regions' (%d).", nreg);
return false;
}
// Construct regions
for (int i = 0; i < nreg; ++i)
regions.push_back(rcRegion((unsigned short) i));
// Find edge of a region and find connections around the contour.
for (int y = 0; y < h; ++y)
{
for (int x = 0; x < w; ++x)
{
const rcCompactCell& c = chf.cells[x+y*w];
for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i)
{
unsigned short r = srcReg[i];
if (r == 0 || r >= nreg)
continue;
rcRegion& reg = regions[r];
reg.spanCount++;
// Update floors.
for (int j = (int)c.index; j < ni; ++j)
{
if (i == j) continue;
unsigned short floorId = srcReg[j];
if (floorId == 0 || floorId >= nreg)
continue;
if (floorId == r)
reg.overlap = true;
addUniqueFloorRegion(reg, floorId);
}
// Have found contour
if (reg.connections.size() > 0)
continue;
reg.areaType = chf.areas[i];
// Check if this cell is next to a border.
int ndir = -1;
for (int dir = 0; dir < 4; ++dir)
{
if (isSolidEdge(chf, srcReg, x, y, i, dir))
{
ndir = dir;
break;
}
}
if (ndir != -1)
{
// The cell is at border.
// Walk around the contour to find all the neighbours.
walkContour(x, y, i, ndir, chf, srcReg, reg.connections);
}
}
}
}
// Remove too small regions.
rcTempVector<int> stack(32);
rcTempVector<int> trace(32);
for (int i = 0; i < nreg; ++i)
{
rcRegion& reg = regions[i];
if (reg.id == 0 || (reg.id & RC_BORDER_REG))
continue;
if (reg.spanCount == 0)
continue;
if (reg.visited)
continue;
// Count the total size of all the connected regions.
// Also keep track of the regions connects to a tile border.
bool connectsToBorder = false;
int spanCount = 0;
stack.clear();
trace.clear();
reg.visited = true;
stack.push_back(i);
while (stack.size())
{
// Pop
int ri = stack.back(); stack.pop_back();
rcRegion& creg = regions[ri];
spanCount += creg.spanCount;
trace.push_back(ri);
for (int j = 0; j < creg.connections.size(); ++j)
{
if (creg.connections[j] & RC_BORDER_REG)
{
connectsToBorder = true;
continue;
}
rcRegion& neireg = regions[creg.connections[j]];
if (neireg.visited)
continue;
if (neireg.id == 0 || (neireg.id & RC_BORDER_REG))
continue;
// Visit
stack.push_back(neireg.id);
neireg.visited = true;
}
}
// If the accumulated regions size is too small, remove it.
// Do not remove areas which connect to tile borders
// as their size cannot be estimated correctly and removing them
// can potentially remove necessary areas.
if (spanCount < minRegionArea && !connectsToBorder)
{
// Kill all visited regions.
for (int j = 0; j < trace.size(); ++j)
{
regions[trace[j]].spanCount = 0;
regions[trace[j]].id = 0;
}
}
}
// Merge too small regions to neighbour regions.
int mergeCount = 0 ;
do
{
mergeCount = 0;
for (int i = 0; i < nreg; ++i)
{
rcRegion& reg = regions[i];
if (reg.id == 0 || (reg.id & RC_BORDER_REG))
continue;
if (reg.overlap)
continue;
if (reg.spanCount == 0)
continue;
// Check to see if the region should be merged.
if (reg.spanCount > mergeRegionSize && isRegionConnectedToBorder(reg))
continue;
// Small region with more than 1 connection.
// Or region which is not connected to a border at all.
// Find smallest neighbour region that connects to this one.
int smallest = 0xfffffff;
unsigned short mergeId = reg.id;
for (int j = 0; j < reg.connections.size(); ++j)
{
if (reg.connections[j] & RC_BORDER_REG) continue;
rcRegion& mreg = regions[reg.connections[j]];
if (mreg.id == 0 || (mreg.id & RC_BORDER_REG) || mreg.overlap) continue;
if (mreg.spanCount < smallest &&
canMergeWithRegion(reg, mreg) &&
canMergeWithRegion(mreg, reg))
{
smallest = mreg.spanCount;
mergeId = mreg.id;
}
}
// Found new id.
if (mergeId != reg.id)
{
unsigned short oldId = reg.id;
rcRegion& target = regions[mergeId];
// Merge neighbours.
if (mergeRegions(target, reg))
{
// Fixup regions pointing to current region.
for (int j = 0; j < nreg; ++j)
{
if (regions[j].id == 0 || (regions[j].id & RC_BORDER_REG)) continue;
// If another region was already merged into current region
// change the nid of the previous region too.
if (regions[j].id == oldId)
regions[j].id = mergeId;
// Replace the current region with the new one if the
// current regions is neighbour.
replaceNeighbour(regions[j], oldId, mergeId);
}
mergeCount++;
}
}
}
}
while (mergeCount > 0);
// Compress region Ids.
for (int i = 0; i < nreg; ++i)
{
regions[i].remap = false;
if (regions[i].id == 0) continue; // Skip nil regions.
if (regions[i].id & RC_BORDER_REG) continue; // Skip external regions.
regions[i].remap = true;
}
unsigned short regIdGen = 0;
for (int i = 0; i < nreg; ++i)
{
if (!regions[i].remap)
continue;
unsigned short oldId = regions[i].id;
unsigned short newId = ++regIdGen;
for (int j = i; j < nreg; ++j)
{
if (regions[j].id == oldId)
{
regions[j].id = newId;
regions[j].remap = false;
}
}
}
maxRegionId = regIdGen;
// Remap regions.
for (int i = 0; i < chf.spanCount; ++i)
{
if ((srcReg[i] & RC_BORDER_REG) == 0)
srcReg[i] = regions[srcReg[i]].id;
}
// Return regions that we found to be overlapping.
for (int i = 0; i < nreg; ++i)
if (regions[i].overlap)
overlaps.push_back(regions[i].id);
return true;
}
...
mergeAndFilterRegions主要分为几个步骤:- 寻找
region的轮廓及其连接信息。- 为每一个
regionId创建一个rcRegion,遍历所有cell上的所有span进行处理,包括:- 将同一
regionId的span数量统计到reg.spanCount中。 - 检查当前
cell上是否有其他span的regionId和当前regionId相同,如果有则设置reg.overlap为true,即有重叠。 - 将当前
cell上所有span的regionId,加入到reg.floors中。 - 设置当前
reg.areaType。 - 通过
isSolidEdge方法,检查四个邻居,如果有一个邻居的regionId是否为其他region或者不可行走,则当前span是当前region的边界。 - 如果当前
span是边界,则通过walkContour方法找到当前region的轮廓,并计算轮廓的region连接信息。
- 将同一
- 为每一个
- 移除过小的
region。- 遍历所有的
region,对每个region进行检查,主要流程:- 设置
spanCount总数量为 0。 - 将当前
regionId加入到stack中,迭代处理。- 从
stack中取出creg,将当前creg.spanCount数量加到spanCount。 - 遍历
creg.connections,对其中每一个neireg进行检查。- 如果
neireg为borderSize的范围,则设置connectsToBorder为true,代表连接到边界。 - 如果
neireg已经访问过,则不再处理。 - 将
neireg标记为已经访问过,并将neireg的regionId加入到stack中。
- 如果
- 继续进行
stack的迭代处理,直到stack处理完成。
- 从
- 设置
- 如果
spanCount小于minRegionArea,并且connectsToBorder为false,则代表当前regionId及其所有connections的regionId组成的整体区域太小,并且没有连接到边界,则将其移除,即当前regionId以及connections的spanCount和regionId都设置为 0。但如果连接到边界,因为无法准确估计其大小,可能导致移除必要的区域,所以会保留。 - 如果移除了
region,后续的region在计算时会直接跳过。计算总数量时,已经移除的region原本的数量也不会计入。
- 遍历所有的
- 合并小的
region到邻居region中。- 遍历所有的
region,对每个region进行检查,主要流程:- 如果
region被移除(reg.spanCount为 0)或者region有重叠(reg.overlap为true),则不处理。 - 从
connections中,通过依次将两个region设置为源region,调用两次canMergeWithRegion方法,找到两者相互都能合并的region。 - 从所有能合并的
region中取spanCount最小的作为目标region,通过mergeRegions方法进行合并。 - 合并成功后,将当前
region、connections、floors中的regionId都更换目标的regionId。
- 如果
- 所有
region处理完成后,如果有成功合并过,则再重复执行一次处理,直到不再有可以合并的region。
- 遍历所有的
- 重新映射
regionId。- 遍历所有的
region,从 1 开始设置剩余的region,将regionId映射为新的区间。
- 遍历所有的
- 应用新的
regionId。- 遍历
srcReg,使用新的regionId进行替换。
- 遍历
- 记录所有重叠的
regionId。- 使用新的
regionId,记录所有有重叠的region。
- 使用新的
- 寻找
walkContour方法的实现如下:
// Recast/Source/RecastRegion.cpp
...
static void walkContour(int x, int y, int i, int dir,
rcCompactHeightfield& chf,
const unsigned short* srcReg,
rcTempVector<int>& cont)
{
int startDir = dir;
int starti = i;
const rcCompactSpan& ss = chf.spans[i];
unsigned short curReg = 0;
if (rcGetCon(ss, dir) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(dir);
const int ay = y + rcGetDirOffsetY(dir);
const int ai = (int)chf.cells[ax+ay*chf.width].index + rcGetCon(ss, dir);
curReg = srcReg[ai];
}
cont.push_back(curReg);
int iter = 0;
while (++iter < 40000)
{
const rcCompactSpan& s = chf.spans[i];
if (isSolidEdge(chf, srcReg, x, y, i, dir))
{
// Choose the edge corner
unsigned short r = 0;
if (rcGetCon(s, dir) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(dir);
const int ay = y + rcGetDirOffsetY(dir);
const int ai = (int)chf.cells[ax+ay*chf.width].index + rcGetCon(s, dir);
r = srcReg[ai];
}
if (r != curReg)
{
curReg = r;
cont.push_back(curReg);
}
dir = (dir+1) & 0x3; // Rotate CW
}
else
{
int ni = -1;
const int nx = x + rcGetDirOffsetX(dir);
const int ny = y + rcGetDirOffsetY(dir);
if (rcGetCon(s, dir) != RC_NOT_CONNECTED)
{
const rcCompactCell& nc = chf.cells[nx+ny*chf.width];
ni = (int)nc.index + rcGetCon(s, dir);
}
if (ni == -1)
{
// Should not happen.
return;
}
x = nx;
y = ny;
i = ni;
dir = (dir+3) & 0x3; // Rotate CCW
}
if (starti == i && startDir == dir)
{
break;
}
}
// Remove adjacent duplicates.
if (cont.size() > 1)
{
for (int j = 0; j < cont.size(); )
{
int nj = (j+1) % cont.size();
if (cont[j] == cont[nj])
{
for (int k = j; k < cont.size()-1; ++k)
cont[k] = cont[k+1];
cont.pop_back();
}
else
++j;
}
}
}
...
walkContour从边界span出发寻找轮廓和连接region,其主要步骤为:- 计算边界
span目标方向邻居的regionId,加入cont中。 - 按照左上右下的方向顺序,从当前
span和方向开始,检查对应的邻居是否为当前region的边界。- 如果是边界,则方向变更为下一个方向,再进行检查。此时如果邻居的
regionId和上一次记录的不同,则将邻居regionId加入cont中。 - 如果不是边界,则将当前
span改为邻居span,方向改为上一个方向,再进行检查。 - 如果当前
span和方向,和起始的相同,则说明回到了起点,轮廓寻找完成,此时所有经过的span组成了整个边界。
- 如果是边界,则方向变更为下一个方向,再进行检查。此时如果邻居的
- 遍历
cont,移除相邻重复的regionId,包括首尾,最终得到一个region的连接regionId列表,即为reg.connections。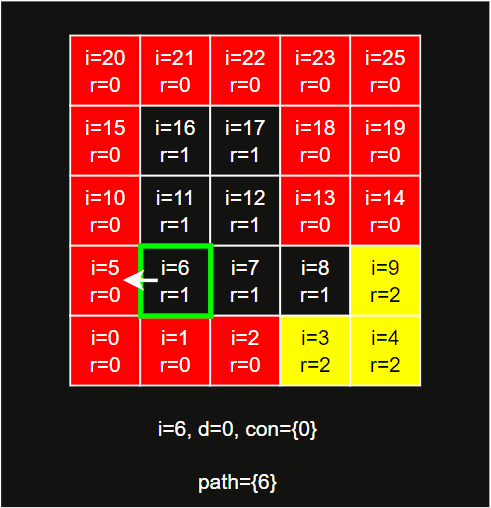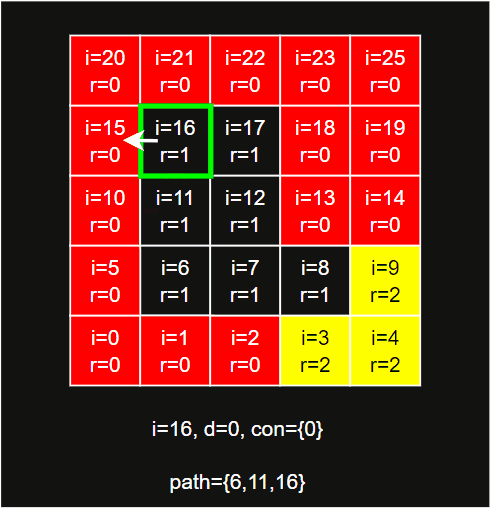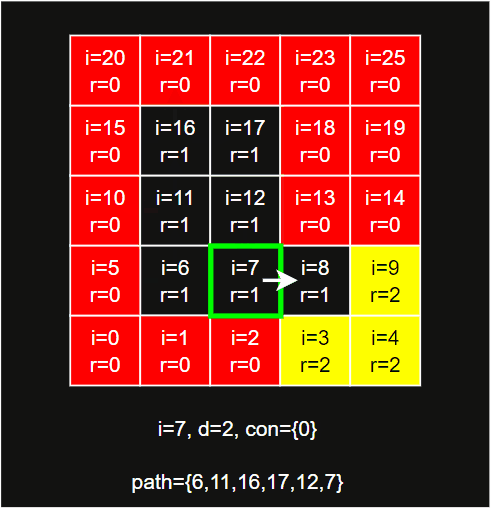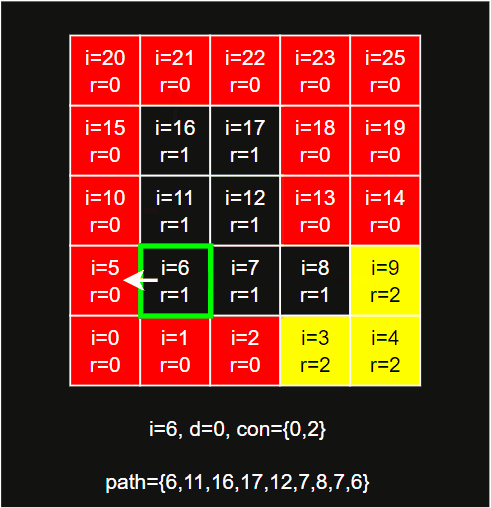
- 计算边界
canMergeWithRegion的实现如下:
// Recast/Source/RecastRegion.cpp
...
static bool canMergeWithRegion(const rcRegion& rega, const rcRegion& regb)
{
if (rega.areaType != regb.areaType)
return false;
int n = 0;
for (int i = 0; i < rega.connections.size(); ++i)
{
if (rega.connections[i] == regb.id)
n++;
}
if (n > 1)
return false;
for (int i = 0; i < rega.floors.size(); ++i)
{
if (rega.floors[i] == regb.id)
return false;
}
return true;
}
...
canMergeWithRegion主要过滤不能合并的情况,包括:- 源
region和目标region的area不同。 - 源
region的connections出现超过一次目标region的regionId,即目标region和源region交界处可能还有其他region。 - 源
region的floors中存在目标region的regionId,即目标region和源region具有出现在同一cell的情况。
- 源
mergeRegions的实现如下:
// Recast/Source/RecastRegion.cpp
...
static bool mergeRegions(rcRegion& rega, rcRegion& regb)
{
unsigned short aid = rega.id;
unsigned short bid = regb.id;
// Duplicate current neighbourhood.
rcTempVector<int> acon;
acon.resize(rega.connections.size());
for (int i = 0; i < rega.connections.size(); ++i)
acon[i] = rega.connections[i];
rcTempVector<int>& bcon = regb.connections;
// Find insertion point on A.
int insa = -1;
for (int i = 0; i < acon.size(); ++i)
{
if (acon[i] == bid)
{
insa = i;
break;
}
}
if (insa == -1)
return false;
// Find insertion point on B.
int insb = -1;
for (int i = 0; i < bcon.size(); ++i)
{
if (bcon[i] == aid)
{
insb = i;
break;
}
}
if (insb == -1)
return false;
// Merge neighbours.
rega.connections.clear();
for (int i = 0, ni = static_cast<int>(acon.size()); i < ni-1; ++i)
{
rega.connections.push_back(acon[(insa+1+i) % ni]);
}
for (int i = 0, ni = static_cast<int>(bcon.size()); i < ni-1; ++i)
{
rega.connections.push_back(bcon[(insb+1+i) % ni]);
}
removeAdjacentNeighbours(rega);
for (int j = 0; j < regb.floors.size(); ++j)
addUniqueFloorRegion(rega, regb.floors[j]);
rega.spanCount += regb.spanCount;
regb.spanCount = 0;
regb.connections.resize(0);
return true;
}
...
mergeRegions合并的主要过程为:- 找出目标
regionId在源region的connections中的索引insa。 - 找出源
regionId在目标region的connections中的索引insb。 - 清空源
region的connections,从insa + 1的位置将源connections重新加入,insa位置不加入,因为和目标region将要合并,所以原来边界中的目标regionId,需要插入目标region的边界连接。 - 从
insb + 1的位置将目标connections加入源connections,同理insb位置不加入。 - 调用
removeAdjacentNeighbours方法,移除源connections中相邻重复的regionId。 - 调用
addUniqueFloorRegion方法,将目标floors加入到源floors中。 - 将目标
spanCount加到源spanCount上,并清空目标region的spanCount和connections,完成合并过程。
- 找出目标
- 以 2D 为例,分水岭划分的全过程如下图:

单调划分
- 单调划分通过
rcBuildRegionsMonotone方法进行,其实现如下:
// Recast/Source/RecastRegion.cpp
...
static const unsigned short RC_NULL_NEI = 0xffff;
struct rcSweepSpan
{
unsigned short rid; // 行索引 id
unsigned short id; // 地区 id
unsigned short ns; // 该地区 id 采样的跨度个数
unsigned short nei; // 邻居的地区 id,通常指下方的 id
};
...
bool rcBuildRegionsMonotone(rcContext* ctx, rcCompactHeightfield& chf,
const int borderSize, const int minRegionArea, const int mergeRegionArea)
{
rcAssert(ctx);
rcScopedTimer timer(ctx, RC_TIMER_BUILD_REGIONS);
const int w = chf.width;
const int h = chf.height;
unsigned short id = 1;
rcScopedDelete<unsigned short> srcReg((unsigned short*)rcAlloc(sizeof(unsigned short)*chf.spanCount, RC_ALLOC_TEMP));
if (!srcReg)
{
ctx->log(RC_LOG_ERROR, "rcBuildRegionsMonotone: Out of memory 'src' (%d).", chf.spanCount);
return false;
}
memset(srcReg,0,sizeof(unsigned short)*chf.spanCount);
const int nsweeps = rcMax(chf.width,chf.height);
rcScopedDelete<rcSweepSpan> sweeps((rcSweepSpan*)rcAlloc(sizeof(rcSweepSpan)*nsweeps, RC_ALLOC_TEMP));
if (!sweeps)
{
ctx->log(RC_LOG_ERROR, "rcBuildRegionsMonotone: Out of memory 'sweeps' (%d).", nsweeps);
return false;
}
// Mark border regions.
if (borderSize > 0)
{
// Make sure border will not overflow.
const int bw = rcMin(w, borderSize);
const int bh = rcMin(h, borderSize);
// Paint regions
paintRectRegion(0, bw, 0, h, id|RC_BORDER_REG, chf, srcReg); id++;
paintRectRegion(w-bw, w, 0, h, id|RC_BORDER_REG, chf, srcReg); id++;
paintRectRegion(0, w, 0, bh, id|RC_BORDER_REG, chf, srcReg); id++;
paintRectRegion(0, w, h-bh, h, id|RC_BORDER_REG, chf, srcReg); id++;
}
chf.borderSize = borderSize;
rcTempVector<int> prev(256);
// Sweep one line at a time.
for (int y = borderSize; y < h-borderSize; ++y)
{
// Collect spans from this row.
prev.resize(id+1);
memset(&prev[0],0,sizeof(int)*id);
unsigned short rid = 1;
for (int x = borderSize; x < w-borderSize; ++x)
{
const rcCompactCell& c = chf.cells[x+y*w];
for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i)
{
const rcCompactSpan& s = chf.spans[i];
if (chf.areas[i] == RC_NULL_AREA) continue;
// -x
unsigned short previd = 0;
if (rcGetCon(s, 0) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(0);
const int ay = y + rcGetDirOffsetY(0);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, 0);
if ((srcReg[ai] & RC_BORDER_REG) == 0 && chf.areas[i] == chf.areas[ai])
previd = srcReg[ai];
}
if (!previd)
{
previd = rid++;
sweeps[previd].rid = previd;
sweeps[previd].ns = 0;
sweeps[previd].nei = 0;
}
// -y
if (rcGetCon(s,3) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(3);
const int ay = y + rcGetDirOffsetY(3);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, 3);
if (srcReg[ai] && (srcReg[ai] & RC_BORDER_REG) == 0 && chf.areas[i] == chf.areas[ai])
{
unsigned short nr = srcReg[ai];
if (!sweeps[previd].nei || sweeps[previd].nei == nr)
{
sweeps[previd].nei = nr;
sweeps[previd].ns++;
prev[nr]++;
}
else
{
sweeps[previd].nei = RC_NULL_NEI;
}
}
}
srcReg[i] = previd;
}
}
// Create unique ID.
for (int i = 1; i < rid; ++i)
{
if (sweeps[i].nei != RC_NULL_NEI && sweeps[i].nei != 0 &&
prev[sweeps[i].nei] == (int)sweeps[i].ns)
{
sweeps[i].id = sweeps[i].nei;
}
else
{
sweeps[i].id = id++;
}
}
// Remap IDs
for (int x = borderSize; x < w-borderSize; ++x)
{
const rcCompactCell& c = chf.cells[x+y*w];
for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i)
{
if (srcReg[i] > 0 && srcReg[i] < rid)
srcReg[i] = sweeps[srcReg[i]].id;
}
}
}
{
rcScopedTimer timerFilter(ctx, RC_TIMER_BUILD_REGIONS_FILTER);
// Merge regions and filter out small regions.
rcTempVector<int> overlaps;
chf.maxRegions = id;
if (!mergeAndFilterRegions(ctx, minRegionArea, mergeRegionArea, chf.maxRegions, chf, srcReg, overlaps))
return false;
// Monotone partitioning does not generate overlapping regions.
}
// Store the result out.
for (int i = 0; i < chf.spanCount; ++i)
chf.spans[i].reg = srcReg[i];
return true;
}
...
rcBuildRegionsMonotone使用了rcSweepSpan结构来记录处理过程的关系,主要流程为:- 通过
paintRectRegion方法,将borderSize范围内的span的region进行标识(id|RC_BORDER_REG),并设置紧密高度场chf.borderSize为borderSize。 - 遍历非
borderSize范围的cell,对其中的每个可行走的span进行处理。- 遍历每一行时,将记录当前行
span被连接的次数prev重置为 0,将rid重置为 1, - 如果当前
span及其左邻居都可行走,且不在borderSize范围,则设置previd为左邻居的regionId。 - 如果
previd为 0,则将其设置为当前未分配给region的rid,并将rid + 1,同时把previd记录到sweeps[pervid]中。 - 如果当前
span及其下邻居都可行走,且不在borderSize范围,且下邻居已分配regionId,则需要设置sweeps[previd].nei。- 如果
sweeps[previd].nei未设置,或者和下邻居的regionId相同,则将sweeps[previd].nei设置为下邻居的regionId。sweeps[previd].ns自增,即记录previd连接到nr的次数。prev[nr]自增,即记录nr被连接的次数。
- 如果
sweeps[previd].nei已设置,并且和下邻居的regionId不同,则将sweeps[previd].nei设置为RC_NULL_NEI,表示有多个邻居。
- 如果
- 将
previd设置为srcReg[i],即作为当前span的regionId。 - 设置完每一行
span的regionId后,遍历所有regionId。- 如果
sweeps[regionId].nei不为 0 且不为RC_NULL_NEI,并且nei的连接和被连接数量相同,则将sweeps[regionId].id设置为下一行的regionId,认为是相同的region。 - 如果
sweeps[regionId].nei为 0 或RC_NULL_NEI,或nei的连接和被连接数量不相同,则将sweeps[regionId].id设置为id,即当前未使用的regionId,认为是不同的region,并将id自增。
- 如果
- 将每一行
sweeps记录的regionId,更新到srcReg中。
- 遍历每一行时,将记录当前行
- 通过
mergeAndFilterRegions,进行region的合并和过滤。 - 将
srcReg记录的最终region信息,应用到紧密高度场中的每一个span,完成划分。
- 通过
- 以 2D 为例,单调划分的全过程如下图:
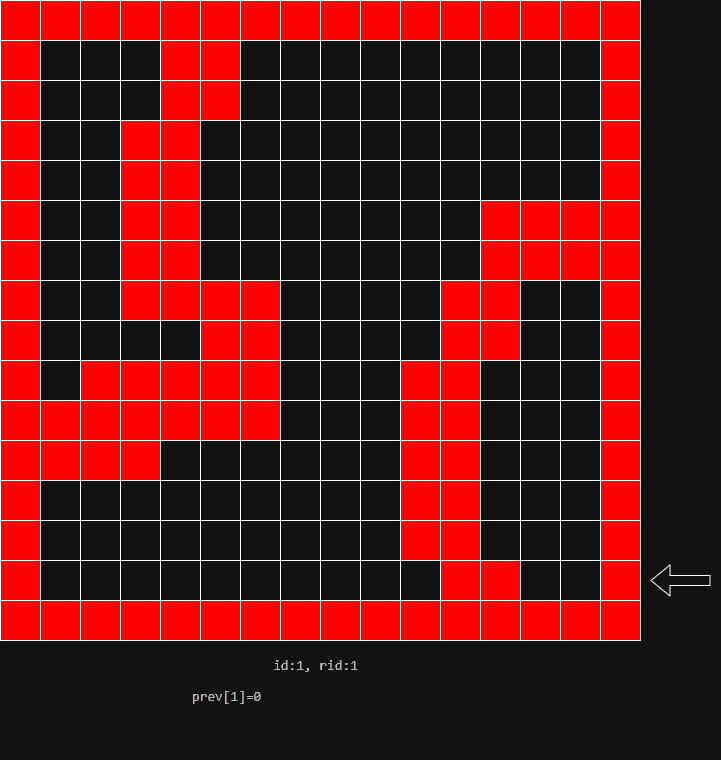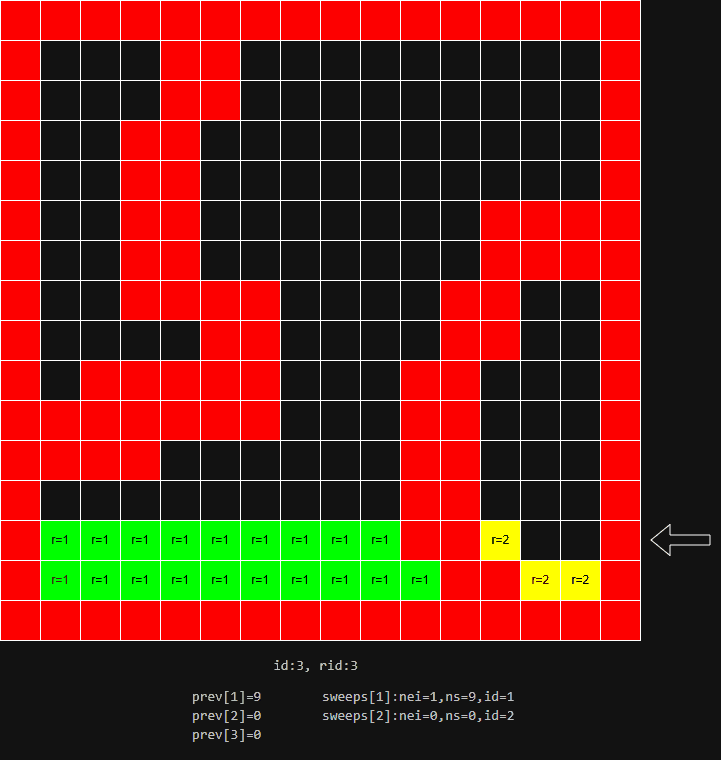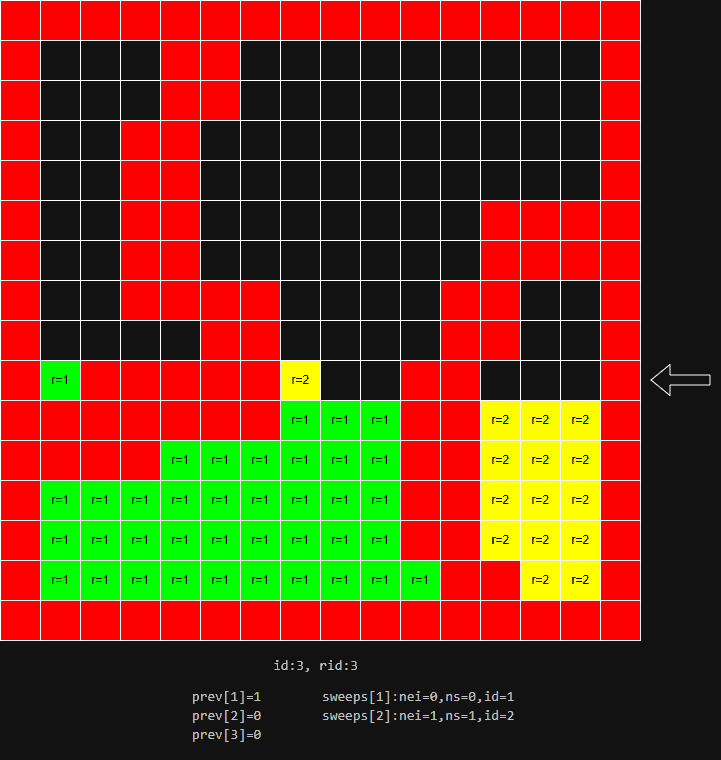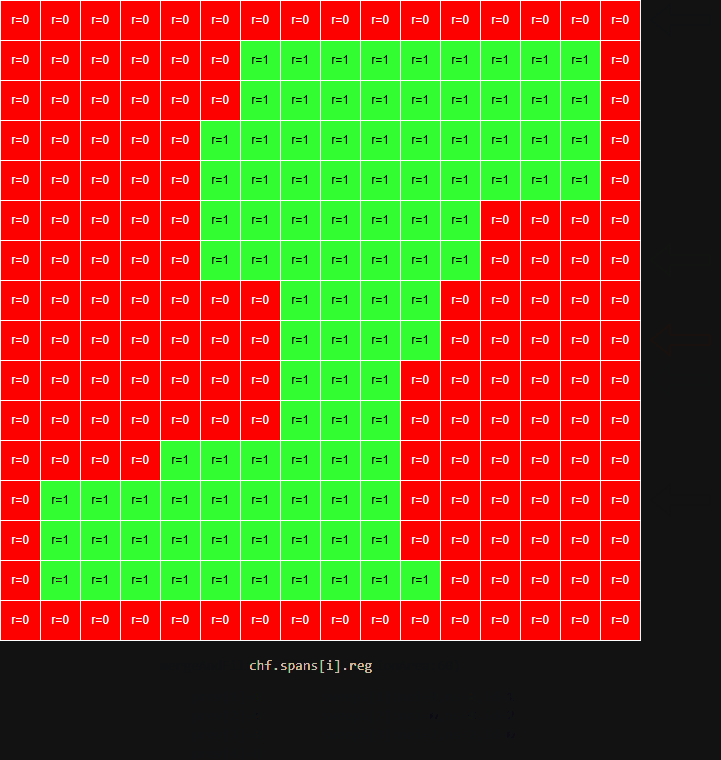
分层划分
- 分层划分通过
rcBuildRegionsLayer方法进行,其实现和单调划分基本一致,唯一不同的,就是单调划分使用mergeAndFilterRegions方法进行合并和过滤,而分层划分使用mergeAndFilterLayerRegions方法,其实现如下:
// Recast/Source/RecastRegion.cpp
...
static bool mergeAndFilterLayerRegions(rcContext* ctx, int minRegionArea,
unsigned short& maxRegionId,
rcCompactHeightfield& chf,
unsigned short* srcReg)
{
const int w = chf.width;
const int h = chf.height;
const int nreg = maxRegionId+1;
rcTempVector<rcRegion> regions;
// Construct regions
if (!regions.reserve(nreg)) {
ctx->log(RC_LOG_ERROR, "mergeAndFilterLayerRegions: Out of memory 'regions' (%d).", nreg);
return false;
}
for (int i = 0; i < nreg; ++i)
regions.push_back(rcRegion((unsigned short) i));
// Find region neighbours and overlapping regions.
rcTempVector<int> lregs(32);
for (int y = 0; y < h; ++y)
{
for (int x = 0; x < w; ++x)
{
const rcCompactCell& c = chf.cells[x+y*w];
lregs.clear();
for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i)
{
const rcCompactSpan& s = chf.spans[i];
const unsigned char area = chf.areas[i];
const unsigned short ri = srcReg[i];
if (ri == 0 || ri >= nreg) continue;
rcRegion& reg = regions[ri];
reg.spanCount++;
reg.areaType = area;
reg.ymin = rcMin(reg.ymin, s.y);
reg.ymax = rcMax(reg.ymax, s.y);
// Collect all region layers.
lregs.push_back(ri);
// Update neighbours
for (int dir = 0; dir < 4; ++dir)
{
if (rcGetCon(s, dir) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(dir);
const int ay = y + rcGetDirOffsetY(dir);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, dir);
const unsigned short rai = srcReg[ai];
if (rai > 0 && rai < nreg && rai != ri)
addUniqueConnection(reg, rai);
if (rai & RC_BORDER_REG)
reg.connectsToBorder = true;
}
}
}
// Update overlapping regions.
for (int i = 0; i < lregs.size()-1; ++i)
{
for (int j = i+1; j < lregs.size(); ++j)
{
if (lregs[i] != lregs[j])
{
rcRegion& ri = regions[lregs[i]];
rcRegion& rj = regions[lregs[j]];
addUniqueFloorRegion(ri, lregs[j]);
addUniqueFloorRegion(rj, lregs[i]);
}
}
}
}
}
// Create 2D layers from regions.
unsigned short layerId = 1;
for (int i = 0; i < nreg; ++i)
regions[i].id = 0;
// Merge montone regions to create non-overlapping areas.
rcTempVector<int> stack(32);
for (int i = 1; i < nreg; ++i)
{
rcRegion& root = regions[i];
// Skip already visited.
if (root.id != 0)
continue;
// Start search.
root.id = layerId;
stack.clear();
stack.push_back(i);
while (stack.size() > 0)
{
// Pop front
rcRegion& reg = regions[stack[0]];
for (int j = 0; j < stack.size()-1; ++j)
stack[j] = stack[j+1];
stack.resize(stack.size()-1);
const int ncons = (int)reg.connections.size();
for (int j = 0; j < ncons; ++j)
{
const int nei = reg.connections[j];
rcRegion& regn = regions[nei];
// Skip already visited.
if (regn.id != 0)
continue;
// Skip if different area type, do not connect regions with different area type.
if (reg.areaType != regn.areaType)
continue;
// Skip if the neighbour is overlapping root region.
bool overlap = false;
for (int k = 0; k < root.floors.size(); k++)
{
if (root.floors[k] == nei)
{
overlap = true;
break;
}
}
if (overlap)
continue;
// Deepen
stack.push_back(nei);
// Mark layer id
regn.id = layerId;
// Merge current layers to root.
for (int k = 0; k < regn.floors.size(); ++k)
addUniqueFloorRegion(root, regn.floors[k]);
root.ymin = rcMin(root.ymin, regn.ymin);
root.ymax = rcMax(root.ymax, regn.ymax);
root.spanCount += regn.spanCount;
regn.spanCount = 0;
root.connectsToBorder = root.connectsToBorder || regn.connectsToBorder;
}
}
layerId++;
}
// Remove small regions
for (int i = 0; i < nreg; ++i)
{
if (regions[i].spanCount > 0 && regions[i].spanCount < minRegionArea && !regions[i].connectsToBorder)
{
unsigned short reg = regions[i].id;
for (int j = 0; j < nreg; ++j)
if (regions[j].id == reg)
regions[j].id = 0;
}
}
// Compress region Ids.
for (int i = 0; i < nreg; ++i)
{
regions[i].remap = false;
if (regions[i].id == 0) continue; // Skip nil regions.
if (regions[i].id & RC_BORDER_REG) continue; // Skip external regions.
regions[i].remap = true;
}
unsigned short regIdGen = 0;
for (int i = 0; i < nreg; ++i)
{
if (!regions[i].remap)
continue;
unsigned short oldId = regions[i].id;
unsigned short newId = ++regIdGen;
for (int j = i; j < nreg; ++j)
{
if (regions[j].id == oldId)
{
regions[j].id = newId;
regions[j].remap = false;
}
}
}
maxRegionId = regIdGen;
// Remap regions.
for (int i = 0; i < chf.spanCount; ++i)
{
if ((srcReg[i] & RC_BORDER_REG) == 0)
srcReg[i] = regions[srcReg[i]].id;
}
return true;
}
...
mergeAndFilterLayerRegions的主要流程为:- 设置
region的基本信息。- 为每一个
regionId创建一个rcRegion,遍历所有cell上的所有span进行处理,包括:- 将同一
regionId的span数量统计到reg.spanCount中。 - 设置当前
reg.areaType。 - 设置当前
reg.ymin和reg.ymax为cell上所有span中的最小最大span.y。 - 检查四个方向的邻居,通过
addUniqueConnection方法将邻居的regionId加入到reg.connections中。如果邻居为borderSize范围的边界,则设置reg.connectsToBorder为true。 - 检查当前
cell上所有连续且regionId不同的span,通过addUniqueFloorRegion方法,分别将regionId加入到彼此的floors列表中。
- 将同一
- 为每一个
- 合并没有重叠的
region。- 初始化
layerId为 1 。 - 将所有
region的id初始化为 0 。 - 遍历每一个
region进行处理。- 如果当前
regionId不为 0 ,则表示该regionId已经处理过,则不再处理。 - 设置当前
region的regionId为layerId。 - 清空
stack,将当前region加入到stack中,进行迭代处理。- 从
stack中取出一个reg,从connections中找到所有未处理过的可行走的邻居regionId,如果当前region的floors中不包含邻居regionId,则代表该regionId没有和当前region重叠,则将邻居region合并到当前region。- 将邻居
regionId加入到stack中。 - 将邻居
region的id设置为layerId,即标记为已处理。 - 将邻居的
floors添加到当前region中。 - 将邻居和当前
region中最小的ymin和最大的ymax设置到当前region中。 - 将邻居的
spanCount加入到当前region,清空邻居的spanCount。 - 如果邻居或当前
region连接到borderSize范围的边界,则设置当前region的connectsToBorder为true。
- 将邻居
- 如果出现重叠,则继续
stack的迭代处理。
- 从
- 处理完一个
regionId,则layerId自增,继续下一个regionId。
- 如果当前
- 初始化
- 移除过小的
region。- 从 1 开始遍历所有的
region,如果spanCount大于 0 且小于minRegionArea,且没有连接到borderSize范围的边界,则此regionId需要被移除。由于上一步中合并后,同一个regionId会处于多个region中,但其中只有一个spanCount大于 0 ,所以需要将所有id为此regionId的region,设置其id为 0。
- 从 1 开始遍历所有的
- 重新映射
regionId。- 遍历所有的
region,从 1 开始设置剩余的region,将regionId映射为新的区间。
- 遍历所有的
- 应用新的
regionId。- 遍历
srcReg,使用新的regionId进行替换。
- 遍历
- 设置
- 以 2D 为例,分层划分的全过程如下图:
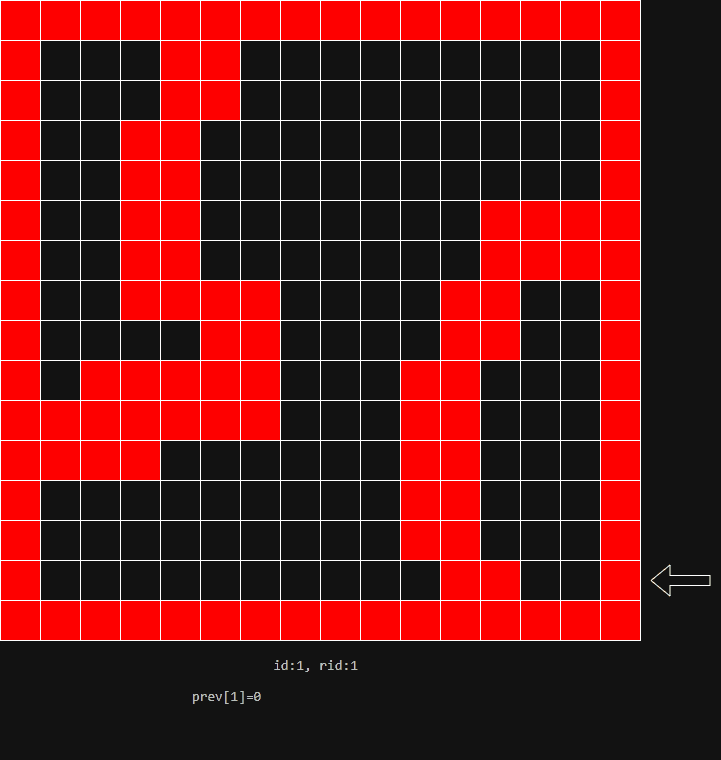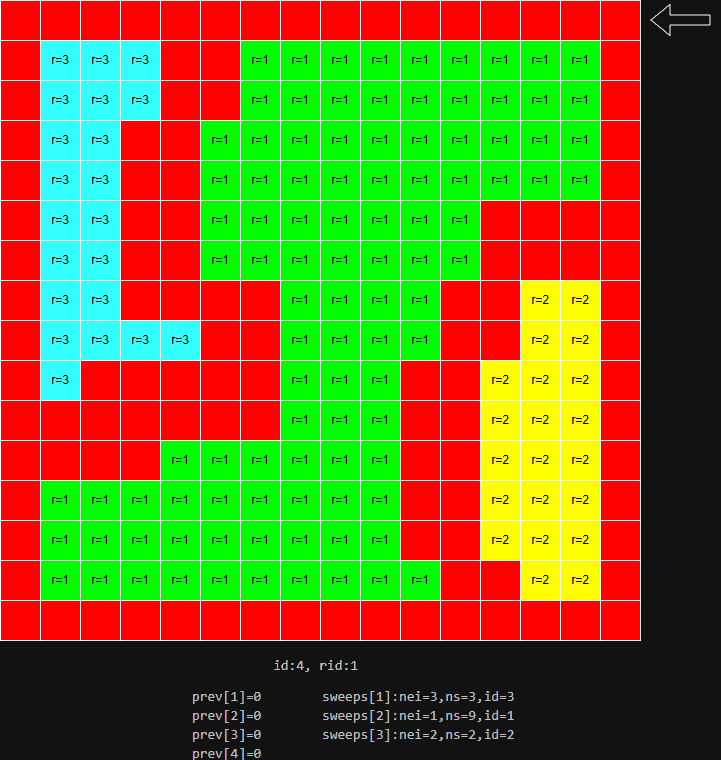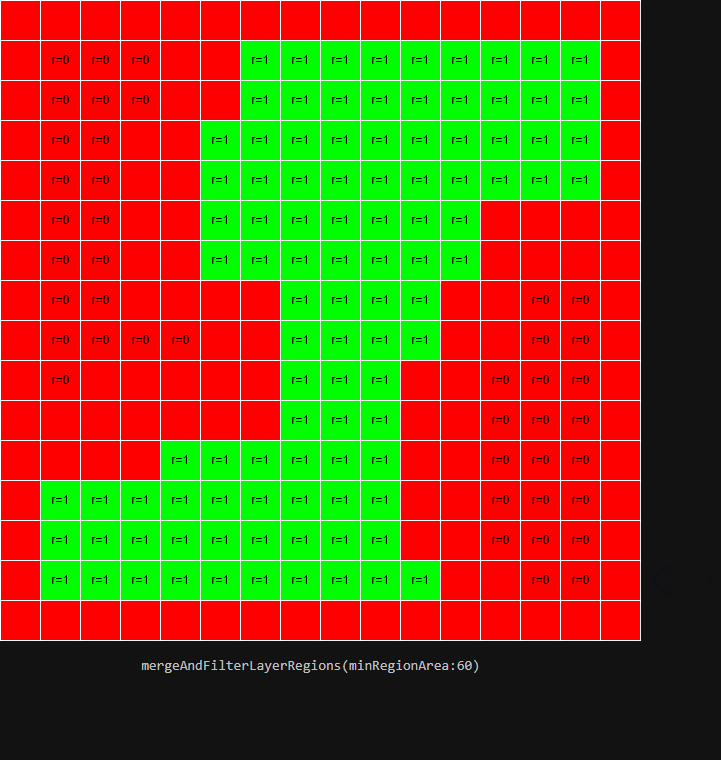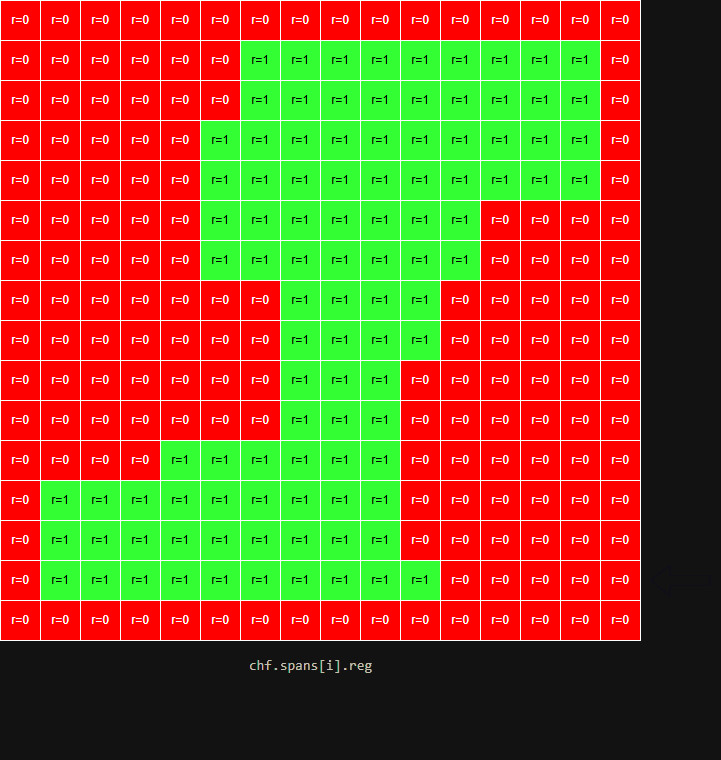
算法对比
| 分水岭划分 | 单调划分 | 分层划分 | |
|---|---|---|---|
| 主要内容 | 计算距离场,洪水填充,按块合并 | 扫描填充,按块合并 | 扫描填充,分层合并 |
| 性能开销 | 高 (需要计算整个距离场,洪水填充过程也需要多次迭代处理) |
低 (扫描填充计算量少,按块合并跳过在同一个 cell 上出现多次的 region ,即仅处理单层 region) |
中 (分层合并需要检查每个 region 的 connections 是否出现在当前 cell ,即需要层级关系,合并后还需要递归检查) |
| 适用场景 | 开放空间和复杂地形 | 简单的平面 | 多层或垂直空间 |
五、查找并简化地区轮廓
- 处理地区轮廓过程,引入了几个新的结构:
rcContourSet:整个高度场的轮廓信息。rcContour:单个轮廓的信息。rcContourRegion:单个region下的轮廓信息。rcContourHole: 单个孔洞的轮廓信息。rcPotentialDiagonal: 对角线信息。
// Recast/Include/Recast.h
...
struct rcContour
{
int* verts; /// 简化后的轮廓顶点
int nverts; /// 简化后的轮廓顶点数量
int* rverts; /// 原始轮廓顶点
int nrverts; /// 原始轮廓顶点数量
unsigned short reg; /// 轮廓的地区id
unsigned char area; /// 轮廓的区域id
};
struct rcContourSet
{
...
rcContour* conts; /// 轮廓列表
int nconts; /// 轮廓数量
float bmin[3]; /// rcHeightfield.bmin + borderSize
float bmax[3]; /// rcHeightfield.bmax - borderSize
float cs; /// 同 rcHeightfield
float ch; /// 同 rcHeightfield
int width; /// rcHeightfield.width - borderSize * 2
int height; /// rcHeightfield.height - borderSize * 2
int borderSize; /// 同 rcConfig::borderSize
float maxError; /// 轮廓简化后的最大边缘误差
...
};
...
// Recast/Source/RecastContour.cpp
...
struct rcContourHole
{
rcContour* contour; /// 孔洞的轮廓
int minx, minz, leftmost; /// 孔洞的轮廓点中最小 x、z 坐标和对应的索引
};
struct rcContourRegion
{
rcContour* outline; /// 当前地区的外轮廓(一个地区只能有一个外轮廓)
rcContourHole* holes; /// 当前地区的孔洞列表
int nholes; /// 当前地区的孔洞数量
};
struct rcPotentialDiagonal
{
int vert; /// 外轮廓的顶点索引
int dist; /// 外轮廓顶点到目标点的距离平方
};
...
- 处理过程主要通过
rcBuildContours方法实现,其代码如下:
// Recast/Source/RecastContour.cpp
...
bool rcBuildContours(rcContext* ctx, const rcCompactHeightfield& chf,
const float maxError, const int maxEdgeLen,
rcContourSet& cset, const int buildFlags)
{
rcAssert(ctx);
const int w = chf.width;
const int h = chf.height;
const int borderSize = chf.borderSize;
rcScopedTimer timer(ctx, RC_TIMER_BUILD_CONTOURS);
rcVcopy(cset.bmin, chf.bmin);
rcVcopy(cset.bmax, chf.bmax);
if (borderSize > 0)
{
// If the heightfield was build with bordersize, remove the offset.
const float pad = borderSize*chf.cs;
cset.bmin[0] += pad;
cset.bmin[2] += pad;
cset.bmax[0] -= pad;
cset.bmax[2] -= pad;
}
cset.cs = chf.cs;
cset.ch = chf.ch;
cset.width = chf.width - chf.borderSize*2;
cset.height = chf.height - chf.borderSize*2;
cset.borderSize = chf.borderSize;
cset.maxError = maxError;
int maxContours = rcMax((int)chf.maxRegions, 8);
cset.conts = (rcContour*)rcAlloc(sizeof(rcContour)*maxContours, RC_ALLOC_PERM);
if (!cset.conts)
return false;
cset.nconts = 0;
rcScopedDelete<unsigned char> flags((unsigned char*)rcAlloc(sizeof(unsigned char)*chf.spanCount, RC_ALLOC_TEMP));
if (!flags)
{
ctx->log(RC_LOG_ERROR, "rcBuildContours: Out of memory 'flags' (%d).", chf.spanCount);
return false;
}
ctx->startTimer(RC_TIMER_BUILD_CONTOURS_TRACE);
// Mark boundaries.
for (int y = 0; y < h; ++y)
{
for (int x = 0; x < w; ++x)
{
const rcCompactCell& c = chf.cells[x+y*w];
for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i)
{
unsigned char res = 0;
const rcCompactSpan& s = chf.spans[i];
if (!chf.spans[i].reg || (chf.spans[i].reg & RC_BORDER_REG))
{
flags[i] = 0;
continue;
}
for (int dir = 0; dir < 4; ++dir)
{
unsigned short r = 0;
if (rcGetCon(s, dir) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(dir);
const int ay = y + rcGetDirOffsetY(dir);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, dir);
r = chf.spans[ai].reg;
}
if (r == chf.spans[i].reg)
res |= (1 << dir);
}
flags[i] = res ^ 0xf; // Inverse, mark non connected edges.
}
}
}
ctx->stopTimer(RC_TIMER_BUILD_CONTOURS_TRACE);
rcTempVector<int> verts(256);
rcTempVector<int> simplified(64);
for (int y = 0; y < h; ++y)
{
for (int x = 0; x < w; ++x)
{
const rcCompactCell& c = chf.cells[x+y*w];
for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i)
{
if (flags[i] == 0 || flags[i] == 0xf)
{
flags[i] = 0;
continue;
}
const unsigned short reg = chf.spans[i].reg;
if (!reg || (reg & RC_BORDER_REG))
continue;
const unsigned char area = chf.areas[i];
verts.clear();
simplified.clear();
ctx->startTimer(RC_TIMER_BUILD_CONTOURS_TRACE);
walkContour(x, y, i, chf, flags, verts);
ctx->stopTimer(RC_TIMER_BUILD_CONTOURS_TRACE);
ctx->startTimer(RC_TIMER_BUILD_CONTOURS_SIMPLIFY);
simplifyContour(verts, simplified, maxError, maxEdgeLen, buildFlags);
removeDegenerateSegments(simplified);
ctx->stopTimer(RC_TIMER_BUILD_CONTOURS_SIMPLIFY);
// Store region->contour remap info.
// Create contour.
if (simplified.size()/4 >= 3)
{
if (cset.nconts >= maxContours)
{
// Allocate more contours.
// This happens when a region has holes.
const int oldMax = maxContours;
maxContours *= 2;
rcContour* newConts = (rcContour*)rcAlloc(sizeof(rcContour)*maxContours, RC_ALLOC_PERM);
for (int j = 0; j < cset.nconts; ++j)
{
newConts[j] = cset.conts[j];
// Reset source pointers to prevent data deletion.
cset.conts[j].verts = 0;
cset.conts[j].rverts = 0;
}
rcFree(cset.conts);
cset.conts = newConts;
ctx->log(RC_LOG_WARNING, "rcBuildContours: Expanding max contours from %d to %d.", oldMax, maxContours);
}
rcContour* cont = &cset.conts[cset.nconts++];
cont->nverts = static_cast<int>(simplified.size()) / 4;
cont->verts = (int*)rcAlloc(sizeof(int)*cont->nverts*4, RC_ALLOC_PERM);
if (!cont->verts)
{
ctx->log(RC_LOG_ERROR, "rcBuildContours: Out of memory 'verts' (%d).", cont->nverts);
return false;
}
memcpy(cont->verts, &simplified[0], sizeof(int)*cont->nverts*4);
if (borderSize > 0)
{
// If the heightfield was build with bordersize, remove the offset.
for (int j = 0; j < cont->nverts; ++j)
{
int* v = &cont->verts[j*4];
v[0] -= borderSize;
v[2] -= borderSize;
}
}
cont->nrverts = static_cast<int>(verts.size()) / 4;
cont->rverts = static_cast<int*>(rcAlloc(sizeof(int) * cont->nrverts * 4, RC_ALLOC_PERM));
if (!cont->rverts)
{
ctx->log(RC_LOG_ERROR, "rcBuildContours: Out of memory 'rverts' (%d).", cont->nrverts);
return false;
}
memcpy(cont->rverts, &verts[0], sizeof(int)*cont->nrverts*4);
if (borderSize > 0)
{
// If the heightfield was build with bordersize, remove the offset.
for (int j = 0; j < cont->nrverts; ++j)
{
int* v = &cont->rverts[j*4];
v[0] -= borderSize;
v[2] -= borderSize;
}
}
cont->reg = reg;
cont->area = area;
}
}
}
}
// Merge holes if needed.
if (cset.nconts > 0)
{
// Calculate winding of all polygons.
rcScopedDelete<signed char> winding((signed char*)rcAlloc(sizeof(signed char)*cset.nconts, RC_ALLOC_TEMP));
if (!winding)
{
ctx->log(RC_LOG_ERROR, "rcBuildContours: Out of memory 'hole' (%d).", cset.nconts);
return false;
}
int nholes = 0;
for (int i = 0; i < cset.nconts; ++i)
{
rcContour& cont = cset.conts[i];
// If the contour is wound backwards, it is a hole.
winding[i] = calcAreaOfPolygon2D(cont.verts, cont.nverts) < 0 ? -1 : 1;
if (winding[i] < 0)
nholes++;
}
if (nholes > 0)
{
// Collect outline contour and holes contours per region.
// We assume that there is one outline and multiple holes.
const int nregions = chf.maxRegions+1;
rcScopedDelete<rcContourRegion> regions((rcContourRegion*)rcAlloc(sizeof(rcContourRegion)*nregions, RC_ALLOC_TEMP));
if (!regions)
{
ctx->log(RC_LOG_ERROR, "rcBuildContours: Out of memory 'regions' (%d).", nregions);
return false;
}
memset(regions, 0, sizeof(rcContourRegion)*nregions);
rcScopedDelete<rcContourHole> holes((rcContourHole*)rcAlloc(sizeof(rcContourHole)*cset.nconts, RC_ALLOC_TEMP));
if (!holes)
{
ctx->log(RC_LOG_ERROR, "rcBuildContours: Out of memory 'holes' (%d).", cset.nconts);
return false;
}
memset(holes, 0, sizeof(rcContourHole)*cset.nconts);
for (int i = 0; i < cset.nconts; ++i)
{
rcContour& cont = cset.conts[i];
// Positively would contours are outlines, negative holes.
if (winding[i] > 0)
{
if (regions[cont.reg].outline)
ctx->log(RC_LOG_ERROR, "rcBuildContours: Multiple outlines for region %d.", cont.reg);
regions[cont.reg].outline = &cont;
}
else
{
regions[cont.reg].nholes++;
}
}
int index = 0;
for (int i = 0; i < nregions; i++)
{
if (regions[i].nholes > 0)
{
regions[i].holes = &holes[index];
index += regions[i].nholes;
regions[i].nholes = 0;
}
}
for (int i = 0; i < cset.nconts; ++i)
{
rcContour& cont = cset.conts[i];
rcContourRegion& reg = regions[cont.reg];
if (winding[i] < 0)
reg.holes[reg.nholes++].contour = &cont;
}
// Finally merge each regions holes into the outline.
for (int i = 0; i < nregions; i++)
{
rcContourRegion& reg = regions[i];
if (!reg.nholes) continue;
if (reg.outline)
{
mergeRegionHoles(ctx, reg);
}
else
{
// The region does not have an outline.
// This can happen if the contour becaomes selfoverlapping because of
// too aggressive simplification settings.
ctx->log(RC_LOG_ERROR, "rcBuildContours: Bad outline for region %d, contour simplification is likely too aggressive.", i);
}
}
}
}
return true;
}
- 处理轮廓的主要步骤如下:
- 初始化
rcContourSet结构cset,根据borderSize设置cset的bmin和bmax,即cset.bmin=chf.bmin+borderSize和cset.bmax=chf.bmax-borderSize。 - 创建
rcContour数组cset.conts,用于存储轮廓数据。 - 遍历每个
cell上的span进行处理。- 如果
span不可通行或者为borderSize范围的边界,则标记当前span的无边界。 - 检查
span的四个邻居,将不可通行或region与自身不同的方向标记为边界。
- 如果
- 再次遍历每个
cell上的span进行处理。- 如果
span无边界或四个方向都为边界,则标记为无边界,不处理。 - 如果
span不可通行或者为borderSize范围的边界,则不处理。 - 通过
walkContour方法找到span的轮廓顶点。 - 通过
simplifyContour方法简化轮廓顶点。 - 通过
removeDegenerateSegments方法,将相邻轮廓顶点中 x、z 坐标相同的顶点移除。 - 由于
cset的基准点发生了变化,所以将简化前后的轮廓顶点减去borderSize后记录到cset中,设置所属的region和area。
- 如果
- 合并孔洞。
- 遍历
cset.conts中的每个轮廓,通过calcAreaOfPolygon2D方法计算轮廓组成的多边形面积,如果小于 0,表示该轮廓为孔洞。 - 如果没有孔洞,则直接跳过。如果存在孔洞,则需要进行处理。
- 遍历所有轮廓,将轮廓按所属的
region分组,将轮廓分为outline和holes。每个region有且只能有一个outline,可以有多个hole。 - 遍历所有
region对应的分组,对有outline和holes的轮廓,调用mergeRegionHoles方法进行合并处理。
- 遍历所有轮廓,将轮廓按所属的
- 遍历
- 初始化
- 处理完成后,通常情况下,
cset.conts中只剩下多个不同region的outline,而holes则都会被合并到outline中。
寻找轮廓顶点
- 寻找轮廓顶点通过
walkContour(RecastContour.cpp)方法实现,而前面分水岭算法中使用的是walkContour(RecastRegion.cpp),两者思路类似,具体实现如下:
// Recast/Source/RecastContour.cpp
...
static void walkContour(int x, int y, int i,
const rcCompactHeightfield& chf,
unsigned char* flags, rcTempVector<int>& points)
{
// Choose the first non-connected edge
unsigned char dir = 0;
while ((flags[i] & (1 << dir)) == 0)
dir++;
unsigned char startDir = dir;
int starti = i;
const unsigned char area = chf.areas[i];
int iter = 0;
while (++iter < 40000)
{
if (flags[i] & (1 << dir))
{
// Choose the edge corner
bool isBorderVertex = false;
bool isAreaBorder = false;
int px = x;
int py = getCornerHeight(x, y, i, dir, chf, isBorderVertex);
int pz = y;
switch(dir)
{
case 0: pz++; break;
case 1: px++; pz++; break;
case 2: px++; break;
}
int r = 0;
const rcCompactSpan& s = chf.spans[i];
if (rcGetCon(s, dir) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(dir);
const int ay = y + rcGetDirOffsetY(dir);
const int ai = (int)chf.cells[ax+ay*chf.width].index + rcGetCon(s, dir);
r = (int)chf.spans[ai].reg;
if (area != chf.areas[ai])
isAreaBorder = true;
}
if (isBorderVertex)
r |= RC_BORDER_VERTEX;
if (isAreaBorder)
r |= RC_AREA_BORDER;
points.push_back(px);
points.push_back(py);
points.push_back(pz);
points.push_back(r);
flags[i] &= ~(1 << dir); // Remove visited edges
dir = (dir+1) & 0x3; // Rotate CW
}
else
{
int ni = -1;
const int nx = x + rcGetDirOffsetX(dir);
const int ny = y + rcGetDirOffsetY(dir);
const rcCompactSpan& s = chf.spans[i];
if (rcGetCon(s, dir) != RC_NOT_CONNECTED)
{
const rcCompactCell& nc = chf.cells[nx+ny*chf.width];
ni = (int)nc.index + rcGetCon(s, dir);
}
if (ni == -1)
{
// Should not happen.
return;
}
x = nx;
y = ny;
i = ni;
dir = (dir+3) & 0x3; // Rotate CCW
}
if (starti == i && startDir == dir)
{
break;
}
}
}
...
- 寻找轮廓顶点过程,使用了
points数组来记录原始轮廓点,每个原始轮廓点使用 4 个整数来表示,依次为 x 、y 、z 和region信息。其中region信息经过二次处理,加上了area边界标记(和邻居的area不同时)和borderSize边界标记(和borderSize相邻或处于其中)。 walkContour的主要步骤如下:- 找到第一个边界方向,作为起始方向,当前
span作为起始span。 - 迭代检查当前
span的当前方向是否为边界方向。- 如果当前方向为边界,则
- 通过
getCornerHeight方法获取当前点的 y 坐标即是否为borderSize边界点,如果方向为 0 或 1,则 z 坐标加 1,如果方向为 1 或 2 ,则 x 坐标加 1。- x 、z 坐标通过边界所在的方向进行偏移,从而保证最终得到的每个轮廓都为右上包含边界,左下不包含边界,避免出现重复。
- 获取当前方向的邻居
span的region信息,将边界信息记录到其中。 - 将当前点的坐标 x 、y 、z 和
region记录到points中,作为一个轮廓顶点。 - 清除当前
span的当前方向标记,后续不再处理该方向。 - 将方向设置为下一个方向。
- 通过
- 如果当前方向不为边界或已经处理过,则
- 将当前方向的邻居
span作为当前span,并设置方向为上一个方向,迭代进行检查处理。
- 将当前方向的邻居
- 如果当前方向为边界,则
- 直到当前
span和起始span相同,且方向相同,则结束迭代,完成轮廓的查找。
- 找到第一个边界方向,作为起始方向,当前
getCornerHeight方法的实现如下:
// Recast/Source/RecastContour.cpp
...
static int getCornerHeight(int x, int y, int i, int dir,
const rcCompactHeightfield& chf,
bool& isBorderVertex)
{
const rcCompactSpan& s = chf.spans[i];
int ch = (int)s.y;
int dirp = (dir+1) & 0x3;
unsigned int regs[4] = {0,0,0,0};
// Combine region and area codes in order to prevent
// border vertices which are in between two areas to be removed.
regs[0] = chf.spans[i].reg | (chf.areas[i] << 16);
if (rcGetCon(s, dir) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(dir);
const int ay = y + rcGetDirOffsetY(dir);
const int ai = (int)chf.cells[ax+ay*chf.width].index + rcGetCon(s, dir);
const rcCompactSpan& as = chf.spans[ai];
ch = rcMax(ch, (int)as.y);
regs[1] = chf.spans[ai].reg | (chf.areas[ai] << 16);
if (rcGetCon(as, dirp) != RC_NOT_CONNECTED)
{
const int ax2 = ax + rcGetDirOffsetX(dirp);
const int ay2 = ay + rcGetDirOffsetY(dirp);
const int ai2 = (int)chf.cells[ax2+ay2*chf.width].index + rcGetCon(as, dirp);
const rcCompactSpan& as2 = chf.spans[ai2];
ch = rcMax(ch, (int)as2.y);
regs[2] = chf.spans[ai2].reg | (chf.areas[ai2] << 16);
}
}
if (rcGetCon(s, dirp) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(dirp);
const int ay = y + rcGetDirOffsetY(dirp);
const int ai = (int)chf.cells[ax+ay*chf.width].index + rcGetCon(s, dirp);
const rcCompactSpan& as = chf.spans[ai];
ch = rcMax(ch, (int)as.y);
regs[3] = chf.spans[ai].reg | (chf.areas[ai] << 16);
if (rcGetCon(as, dir) != RC_NOT_CONNECTED)
{
const int ax2 = ax + rcGetDirOffsetX(dir);
const int ay2 = ay + rcGetDirOffsetY(dir);
const int ai2 = (int)chf.cells[ax2+ay2*chf.width].index + rcGetCon(as, dir);
const rcCompactSpan& as2 = chf.spans[ai2];
ch = rcMax(ch, (int)as2.y);
regs[2] = chf.spans[ai2].reg | (chf.areas[ai2] << 16);
}
}
// Check if the vertex is special edge vertex, these vertices will be removed later.
for (int j = 0; j < 4; ++j)
{
const int a = j;
const int b = (j+1) & 0x3;
const int c = (j+2) & 0x3;
const int d = (j+3) & 0x3;
// The vertex is a border vertex there are two same exterior cells in a row,
// followed by two interior cells and none of the regions are out of bounds.
const bool twoSameExts = (regs[a] & regs[b] & RC_BORDER_REG) != 0 && regs[a] == regs[b];
const bool twoInts = ((regs[c] | regs[d]) & RC_BORDER_REG) == 0;
const bool intsSameArea = (regs[c]>>16) == (regs[d]>>16);
const bool noZeros = regs[a] != 0 && regs[b] != 0 && regs[c] != 0 && regs[d] != 0;
if (twoSameExts && twoInts && intsSameArea && noZeros)
{
isBorderVertex = true;
break;
}
}
return ch;
}
...
getCornerHeight的主要步骤为:- 初始化 y 坐标为当前
span的 y 坐标。 - 如果当前方向邻居
span可通行,则取邻居span的 y 坐标和当前 y 坐标中的最大值作为当前 y 坐标。 - 如果当前方向邻居
span可通行,且邻居span的下一个方向邻居span可通行,则同样取其 y 坐标和当前 y 坐标中的最大值作为当前 y 坐标。 - 如果下一个方向邻居
span可通行,则取其 y 坐标和当前 y 坐标中的最大值作为当前 y 坐标。 - 如果下一个方向邻居
span可通行,且当前方向邻居span可通行,则同样取其 y 坐标和当前 y 坐标中的最大值作为当前 y 坐标。 - 检查完成后,当前 y 坐标即为轮廓点的 y 坐标。
- 当前
span、当前方向邻居span、当前方向邻居span的下一个方向邻居span、下一个方向邻居span,保持先后顺序,每次以其中一个为起始进行迭代检查。- 以当前的起始算起,如果前两个的
region相同且为borderSize边界,后两个的area相同且不为borderSize边界,且四个span都可通行,则当前点为borderSize边界点。
- 以当前的起始算起,如果前两个的
- 初始化 y 坐标为当前
简化轮廓顶点
- 简化轮廓顶点的方法
simplifyContour实现如下:
// Recast/Source/RecastContour.cpp
...
static void simplifyContour(rcTempVector<int>& points, rcTempVector<int>& simplified,
const float maxError, const int maxEdgeLen, const int buildFlags)
{
// Add initial points.
bool hasConnections = false;
for (int i = 0; i < points.size(); i += 4)
{
if ((points[i+3] & RC_CONTOUR_REG_MASK) != 0)
{
hasConnections = true;
break;
}
}
if (hasConnections)
{
// The contour has some portals to other regions.
// Add a new point to every location where the region changes.
for (int i = 0, ni = static_cast<int>(points.size()) / 4; i < ni; ++i)
{
int ii = (i+1) % ni;
const bool differentRegs = (points[i*4+3] & RC_CONTOUR_REG_MASK) != (points[ii*4+3] & RC_CONTOUR_REG_MASK);
const bool areaBorders = (points[i*4+3] & RC_AREA_BORDER) != (points[ii*4+3] & RC_AREA_BORDER);
if (differentRegs || areaBorders)
{
simplified.push_back(points[i*4+0]);
simplified.push_back(points[i*4+1]);
simplified.push_back(points[i*4+2]);
simplified.push_back(i);
}
}
}
if (simplified.size() == 0)
{
// If there is no connections at all,
// create some initial points for the simplification process.
// Find lower-left and upper-right vertices of the contour.
int llx = points[0];
int lly = points[1];
int llz = points[2];
int lli = 0;
int urx = points[0];
int ury = points[1];
int urz = points[2];
int uri = 0;
for (int i = 0; i < points.size(); i += 4)
{
int x = points[i+0];
int y = points[i+1];
int z = points[i+2];
if (x < llx || (x == llx && z < llz))
{
llx = x;
lly = y;
llz = z;
lli = i/4;
}
if (x > urx || (x == urx && z > urz))
{
urx = x;
ury = y;
urz = z;
uri = i/4;
}
}
simplified.push_back(llx);
simplified.push_back(lly);
simplified.push_back(llz);
simplified.push_back(lli);
simplified.push_back(urx);
simplified.push_back(ury);
simplified.push_back(urz);
simplified.push_back(uri);
}
// Add points until all raw points are within
// error tolerance to the simplified shape.
const int pn = static_cast<int>(points.size()) / 4;
for (int i = 0; i < simplified.size()/4; )
{
int ii = (i+1) % (simplified.size()/4);
int ax = simplified[i*4+0];
int az = simplified[i*4+2];
int ai = simplified[i*4+3];
int bx = simplified[ii*4+0];
int bz = simplified[ii*4+2];
int bi = simplified[ii*4+3];
// Find maximum deviation from the segment.
float maxd = 0;
int maxi = -1;
int ci, cinc, endi;
// Traverse the segment in lexilogical order so that the
// max deviation is calculated similarly when traversing
// opposite segments.
if (bx > ax || (bx == ax && bz > az))
{
cinc = 1;
ci = (ai+cinc) % pn;
endi = bi;
}
else
{
cinc = pn-1;
ci = (bi+cinc) % pn;
endi = ai;
rcSwap(ax, bx);
rcSwap(az, bz);
}
// Tessellate only outer edges or edges between areas.
if ((points[ci*4+3] & RC_CONTOUR_REG_MASK) == 0 ||
(points[ci*4+3] & RC_AREA_BORDER))
{
while (ci != endi)
{
float d = distancePtSeg(points[ci*4+0], points[ci*4+2], ax, az, bx, bz);
if (d > maxd)
{
maxd = d;
maxi = ci;
}
ci = (ci+cinc) % pn;
}
}
// If the max deviation is larger than accepted error,
// add new point, else continue to next segment.
if (maxi != -1 && maxd > (maxError*maxError))
{
// Add space for the new point.
simplified.resize(simplified.size()+4);
const int n = static_cast<int>(simplified.size()) / 4;
for (int j = n-1; j > i; --j)
{
simplified[j*4+0] = simplified[(j-1)*4+0];
simplified[j*4+1] = simplified[(j-1)*4+1];
simplified[j*4+2] = simplified[(j-1)*4+2];
simplified[j*4+3] = simplified[(j-1)*4+3];
}
// Add the point.
simplified[(i+1)*4+0] = points[maxi*4+0];
simplified[(i+1)*4+1] = points[maxi*4+1];
simplified[(i+1)*4+2] = points[maxi*4+2];
simplified[(i+1)*4+3] = maxi;
}
else
{
++i;
}
}
// Split too long edges.
if (maxEdgeLen > 0 && (buildFlags & (RC_CONTOUR_TESS_WALL_EDGES|RC_CONTOUR_TESS_AREA_EDGES)) != 0)
{
for (int i = 0; i < simplified.size()/4; )
{
const int ii = (i+1) % (simplified.size()/4);
const int ax = simplified[i*4+0];
const int az = simplified[i*4+2];
const int ai = simplified[i*4+3];
const int bx = simplified[ii*4+0];
const int bz = simplified[ii*4+2];
const int bi = simplified[ii*4+3];
// Find maximum deviation from the segment.
int maxi = -1;
int ci = (ai+1) % pn;
// Tessellate only outer edges or edges between areas.
bool tess = false;
// Wall edges.
if ((buildFlags & RC_CONTOUR_TESS_WALL_EDGES) && (points[ci*4+3] & RC_CONTOUR_REG_MASK) == 0)
tess = true;
// Edges between areas.
if ((buildFlags & RC_CONTOUR_TESS_AREA_EDGES) && (points[ci*4+3] & RC_AREA_BORDER))
tess = true;
if (tess)
{
int dx = bx - ax;
int dz = bz - az;
if (dx*dx + dz*dz > maxEdgeLen*maxEdgeLen)
{
// Round based on the segments in lexilogical order so that the
// max tesselation is consistent regardless in which direction
// segments are traversed.
const int n = bi < ai ? (bi+pn - ai) : (bi - ai);
if (n > 1)
{
if (bx > ax || (bx == ax && bz > az))
maxi = (ai + n/2) % pn;
else
maxi = (ai + (n+1)/2) % pn;
}
}
}
// If the max deviation is larger than accepted error,
// add new point, else continue to next segment.
if (maxi != -1)
{
// Add space for the new point.
simplified.resize(simplified.size()+4);
const int n = static_cast<int>(simplified.size()) / 4;
for (int j = n-1; j > i; --j)
{
simplified[j*4+0] = simplified[(j-1)*4+0];
simplified[j*4+1] = simplified[(j-1)*4+1];
simplified[j*4+2] = simplified[(j-1)*4+2];
simplified[j*4+3] = simplified[(j-1)*4+3];
}
// Add the point.
simplified[(i+1)*4+0] = points[maxi*4+0];
simplified[(i+1)*4+1] = points[maxi*4+1];
simplified[(i+1)*4+2] = points[maxi*4+2];
simplified[(i+1)*4+3] = maxi;
}
else
{
++i;
}
}
}
for (int i = 0; i < simplified.size()/4; ++i)
{
// The edge vertex flag is take from the current raw point,
// and the neighbour region is take from the next raw point.
const int ai = (simplified[i*4+3]+1) % pn;
const int bi = simplified[i*4+3];
simplified[i*4+3] = (points[ai*4+3] & (RC_CONTOUR_REG_MASK|RC_AREA_BORDER)) | (points[bi*4+3] & RC_BORDER_VERTEX);
}
}
...
- 简化轮廓的过程使用了
simplified数组记录简化后的轮廓点信息,每个简化点使用 4 个整数表示,依次为 x 、y 、z 和在原始轮廓points中的索引信息,简化完成后再将索引信息替换为region信息。 simplifyContour的过程如下:- 如果轮廓中存在可行走的点,则依次遍历每个原轮廓点,如果当前点和下个点的
region或area不同,则将当前点加入到简化轮廓列表simplified中。 - 如果
simplified为空,即没有找到region或area不同的点,则将轮廓的左下点和右上点加入到simplified中。 - 遍历
simplified组成的每一条边,找到所有region不为 0 或者是area边界的原轮廓点,通过distancePtSeg方法计算这些原轮廓点到这条边的距离,从中找到距离最大的原轮廓点,如果该距离大于maxError,则将该原轮廓点插入到simplified中此边的中间,否则跳过此边。 - 如果设置了
maxEdgeLen且设置了需要进行细分,则依次遍历simplified组成的每一条边.- 如果边的起点的下一个原始轮廓点的
region不为 0 且设置了细分墙边(RC_CONTOUR_TESS_WALL_EDGES),或者下一个原始轮廓点为area边界且设置了细分区域边(RC_CONTOUR_TESS_AREA_EDGES),则此边需要进行细分处理。 - 对于需要细分处理的边,如果边的长度大于
maxEdgeLen,且边上除端点外的原始轮廓点数量大于 1,则取中间的原始轮廓点,插入到simplified中此边的中间。
- 如果边的起点的下一个原始轮廓点的
- 遍历
simplified的每个点,将索引信息替换为region信息。
- 如果轮廓中存在可行走的点,则依次遍历每个原轮廓点,如果当前点和下个点的
查找孔洞
- 通过
calcAreaOfPolygon2D方法,在所有轮廓中识别出孔洞,其实现如下:
// Recast/Source/RecastContour.cpp
...
static int calcAreaOfPolygon2D(const int* verts, const int nverts)
{
int area = 0;
for (int i = 0, j = nverts-1; i < nverts; j=i++)
{
const int* vi = &verts[i*4];
const int* vj = &verts[j*4];
area += vi[0] * vj[2] - vj[0] * vi[2];
}
return (area+1) / 2;
}
...
- 查找轮廓的时候是按顺时针方向进行得到的结果,而多边形的顶点是按逆时针方向排序的,所以计算面积时需要使用轮廓的当前顶点和上一个顶点来计算。
- 遍历每个顶点,根据原点和当前顶点的向量,以及原点到上一个顶点的向量,两者的叉积得到三个点组成的三角形的面积,而所有三角形面积之和即为多边形的面积。其中,叉积为正,表示从向量 1 到向量 2 为逆时针旋转。叉积为负,表示从向量 1 到向量 2 为顺时针旋转。
- 如果最终多边形的面积为负,则表示该轮廓为逆时针方向,即为孔洞。相反,如果面积为正,则表示该轮廓为外轮廓。
合并孔洞
- 通过
mergeRegionHoles方法,将孔洞合并到外轮廓中,其实现如下:
// Recast/Source/RecastContour.cpp
...
static void mergeRegionHoles(rcContext* ctx, rcContourRegion& region)
{
// Sort holes from left to right.
for (int i = 0; i < region.nholes; i++)
findLeftMostVertex(region.holes[i].contour, ®ion.holes[i].minx, ®ion.holes[i].minz, ®ion.holes[i].leftmost);
qsort(region.holes, region.nholes, sizeof(rcContourHole), compareHoles);
int maxVerts = region.outline->nverts;
for (int i = 0; i < region.nholes; i++)
maxVerts += region.holes[i].contour->nverts;
rcScopedDelete<rcPotentialDiagonal> diags((rcPotentialDiagonal*)rcAlloc(sizeof(rcPotentialDiagonal)*maxVerts, RC_ALLOC_TEMP));
if (!diags)
{
ctx->log(RC_LOG_WARNING, "mergeRegionHoles: Failed to allocated diags %d.", maxVerts);
return;
}
rcContour* outline = region.outline;
// Merge holes into the outline one by one.
for (int i = 0; i < region.nholes; i++)
{
rcContour* hole = region.holes[i].contour;
int index = -1;
int bestVertex = region.holes[i].leftmost;
for (int iter = 0; iter < hole->nverts; iter++)
{
// Find potential diagonals.
// The 'best' vertex must be in the cone described by 3 consecutive vertices of the outline.
// ..o j-1
// |
// | * best
// |
// j o-----o j+1
// :
int ndiags = 0;
const int* corner = &hole->verts[bestVertex*4];
for (int j = 0; j < outline->nverts; j++)
{
if (inCone(j, outline->nverts, outline->verts, corner))
{
int dx = outline->verts[j*4+0] - corner[0];
int dz = outline->verts[j*4+2] - corner[2];
diags[ndiags].vert = j;
diags[ndiags].dist = dx*dx + dz*dz;
ndiags++;
}
}
// Sort potential diagonals by distance, we want to make the connection as short as possible.
qsort(diags, ndiags, sizeof(rcPotentialDiagonal), compareDiagDist);
// Find a diagonal that is not intersecting the outline not the remaining holes.
index = -1;
for (int j = 0; j < ndiags; j++)
{
const int* pt = &outline->verts[diags[j].vert*4];
bool intersect = intersectSegContour(pt, corner, diags[i].vert, outline->nverts, outline->verts); //这里的 diags[i] 应该是错误的,实际应该是 diags[j]
for (int k = i; k < region.nholes && !intersect; k++)
intersect |= intersectSegContour(pt, corner, -1, region.holes[k].contour->nverts, region.holes[k].contour->verts);
if (!intersect)
{
index = diags[j].vert;
break;
}
}
// If found non-intersecting diagonal, stop looking.
if (index != -1)
break;
// All the potential diagonals for the current vertex were intersecting, try next vertex.
bestVertex = (bestVertex + 1) % hole->nverts;
}
if (index == -1)
{
ctx->log(RC_LOG_WARNING, "mergeHoles: Failed to find merge points for %p and %p.", region.outline, hole);
continue;
}
if (!mergeContours(*region.outline, *hole, index, bestVertex))
{
ctx->log(RC_LOG_WARNING, "mergeHoles: Failed to merge contours %p and %p.", region.outline, hole);
continue;
}
}
}
...
mergeRegionHoles合并的主要步骤如下:- 遍历当前
region的每个hole,设置每个hole的左下点坐标及索引,并将hole按照左下点坐标进行排序,越靠近左下的排在前面。 - 遍历当前
region的每个hole,对每个hole进行处理。- 从当前
hole最左下点开始,依次将每个点为拐角点,迭代进行检查。- 遍历当前
region外轮廓的每个点,通过inCone方法判断拐角点是否在当前外轮廓点及其前后两个点组成的角度区域内,如果在,则计算该点和拐角点的距离,并将该点加入到diags数组中。 - 对
diags数组按照距离从小到大进行排序。 - 遍历
diags数组,通过intersectSegContour方法依次检查diags[j]和拐角点的线段的包围盒是否和outline中不包含diags[j]的边的包围盒不相交,并且和剩余的hole的任意边的包围盒也不相交,如果都不相交,则diags[j]为合并点,结束迭代。 - 如果没有找到合并点,则将下一个点设置为拐角点,继续迭代。
- 遍历当前
- 如果找到了合并点,则通过
mergeContours方法将hole合并到outline中,检查相交情况时,则不需要再检查此hole,因为已经加入到outline中,检查和outline的相交情况已经同时处理了。(如果没有找到合并点,后续也没有重新检查未被合并的hole的相交情况,可能存在问题?)
- 从当前
- 遍历当前
inCone方法的实现如下:
// Recast/Source/RecastContour.cpp
...
static bool inCone(int i, int n, const int* verts, const int* pj)
{
const int* pi = &verts[i * 4];
const int* pi1 = &verts[next(i, n) * 4];
const int* pin1 = &verts[prev(i, n) * 4];
// If P[i] is a convex vertex [ i+1 left or on (i-1,i) ].
if (leftOn(pin1, pi, pi1))
return left(pi, pj, pin1) && left(pj, pi, pi1);
// Assume (i-1,i,i+1) not collinear.
// else P[i] is reflex.
return !(leftOn(pi, pj, pi1) && leftOn(pj, pi, pin1));
}
...
inline int area2(const int* a, const int* b, const int* c)
{
return (b[0] - a[0]) * (c[2] - a[2]) - (c[0] - a[0]) * (b[2] - a[2]);
}
// Returns true iff c is strictly to the left of the directed
// line through a to b.
inline bool left(const int* a, const int* b, const int* c)
{
return area2(a, b, c) < 0;
}
inline bool leftOn(const int* a, const int* b, const int* c)
{
return area2(a, b, c) <= 0;
}
...
inCone方法通过当前顶点、上一个顶点、下一个顶点组成的角,判断目标点是否在角组成的范围内。left方法通过向量 AB 和向量 AC 的叉积,来判断点所在的位置。通常情况下,如果向量叉积为正,则点 C 在向量 AB 的逆时针方向,即左侧,如果为负,则点 C 在向量 AB 的顺时针方向,即右侧。而这里的left方法判断相反,但前面提到,轮廓顶点是按顺时针方向得到的,多边形顶点则是按逆时针方向排序的,而这里使用的是轮廓的顶点顺序,因此left代表的是多边形排序的左侧,所以结果上也是正确的。intersectSegContour方法的实现如下:
// Recast/Source/RecastContour.cpp
...
inline bool collinear(const int* a, const int* b, const int* c)
{
return area2(a, b, c) == 0;
}
static bool intersectProp(const int* a, const int* b, const int* c, const int* d)
{
// Eliminate improper cases.
if (collinear(a,b,c) || collinear(a,b,d) ||
collinear(c,d,a) || collinear(c,d,b))
return false;
return (left(a,b,c) ^ left(a,b,d)) && (left(c,d,a) ^ left(c,d,b));
}
// Returns T iff (a,b,c) are collinear and point c lies
// on the closed segment ab.
static bool between(const int* a, const int* b, const int* c)
{
if (!collinear(a, b, c))
return false;
// If ab not vertical, check betweenness on x; else on y.
if (a[0] != b[0])
return ((a[0] <= c[0]) && (c[0] <= b[0])) || ((a[0] >= c[0]) && (c[0] >= b[0]));
else
return ((a[2] <= c[2]) && (c[2] <= b[2])) || ((a[2] >= c[2]) && (c[2] >= b[2]));
}
// Returns true iff segments ab and cd intersect, properly or improperly.
static bool intersect(const int* a, const int* b, const int* c, const int* d)
{
if (intersectProp(a, b, c, d))
return true;
else if (between(a, b, c) || between(a, b, d) ||
between(c, d, a) || between(c, d, b))
return true;
else
return false;
}
static bool vequal(const int* a, const int* b)
{
return a[0] == b[0] && a[2] == b[2];
}
static bool intersectSegContour(const int* d0, const int* d1, int i, int n, const int* verts)
{
// For each edge (k,k+1) of P
for (int k = 0; k < n; k++)
{
int k1 = next(k, n);
// Skip edges incident to i.
if (i == k || i == k1)
continue;
const int* p0 = &verts[k * 4];
const int* p1 = &verts[k1 * 4];
if (vequal(d0, p0) || vequal(d1, p0) || vequal(d0, p1) || vequal(d1, p1))
continue;
if (intersect(d0, d1, p0, p1))
return true;
}
return false;
}
intersectSegContour方法通过传入的两个点组成的线段,遍历顶点数组中的每条边,跳过和输入点及指定索引相同的顶点所在的边,通过intersect方法判断在 xz 平面上线段的包围盒和边的包围盒是否相交。同样,也是通过向量叉积的方式进行计算,当两条线段中各自的顶点,都处在另一线段的两侧,说明两条线段直接相交。当两条线段中的任一顶点,处在另一条线段的包围盒中,则两条线段的包围盒相交。mergeContours方法的实现如下:
// Recast/Source/RecastContour.cpp
static bool mergeContours(rcContour& ca, rcContour& cb, int ia, int ib)
{
const int maxVerts = ca.nverts + cb.nverts + 2;
int* verts = (int*)rcAlloc(sizeof(int)*maxVerts*4, RC_ALLOC_PERM);
if (!verts)
return false;
int nv = 0;
// Copy contour A.
for (int i = 0; i <= ca.nverts; ++i)
{
int* dst = &verts[nv*4];
const int* src = &ca.verts[((ia+i)%ca.nverts)*4];
dst[0] = src[0];
dst[1] = src[1];
dst[2] = src[2];
dst[3] = src[3];
nv++;
}
// Copy contour B
for (int i = 0; i <= cb.nverts; ++i)
{
int* dst = &verts[nv*4];
const int* src = &cb.verts[((ib+i)%cb.nverts)*4];
dst[0] = src[0];
dst[1] = src[1];
dst[2] = src[2];
dst[3] = src[3];
nv++;
}
rcFree(ca.verts);
ca.verts = verts;
ca.nverts = nv;
rcFree(cb.verts);
cb.verts = 0;
cb.nverts = 0;
return true;
}
...
mergeContours方法,从outline找到的合并点起,将outline的所有点加入的到新的轮廓中,再把合并点加入,接着从hole的拐角点起,将hole的所有点加入,再把拐角点加入,得到合并后的轮廓。每个轮廓都将起始点重复加入,确保闭合。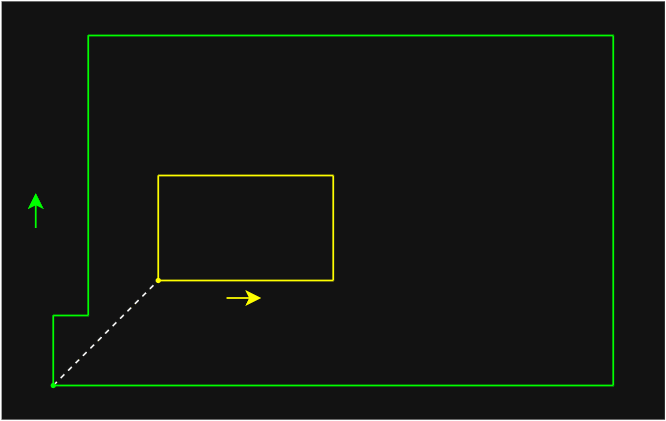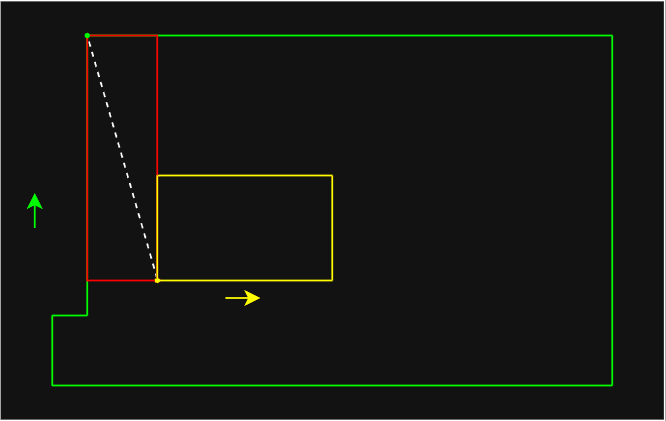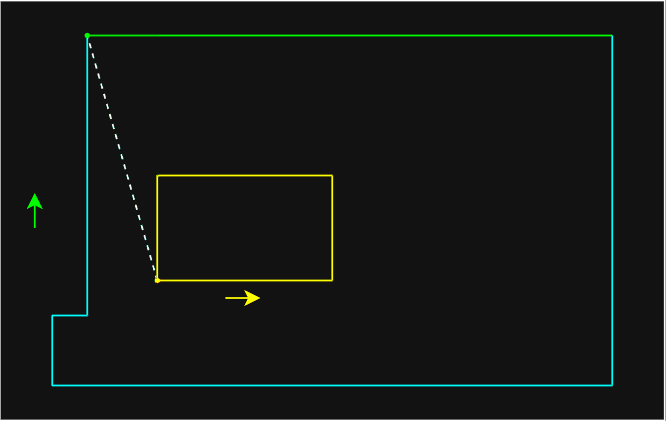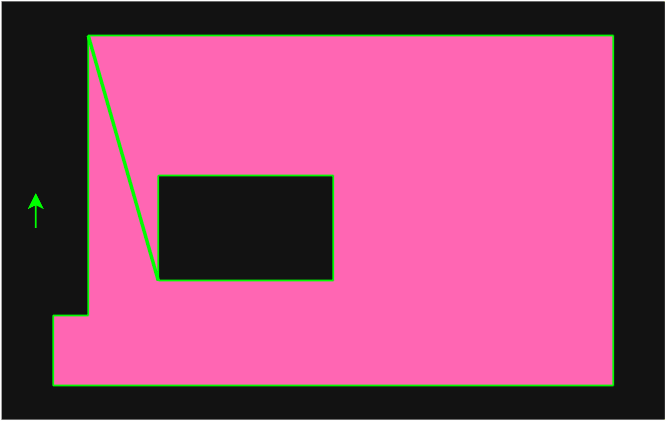
六、建立多边形网格
- 建立多边形网格过程,使用
rcPolyMesh结构保存多边形网格数据,其定义如下:
// Recast/Include/Recast.h
...
struct rcPolyMesh
{
...
unsigned short* verts; /// 顶点坐标,每个顶点占 3 位
unsigned short* polys; /// 多边形顶点索引,以及其每条边的邻居多边形索引,尺寸为 npolys * nvp * 2,[0 , npolys * nvp - 1] 为顶点索引,[npolys * nvp , npolys * nvp * 2 - 1] 为邻居多边形索引
unsigned short* regs; /// 每个多边形的地区
unsigned short* flags; /// 每个多边形的标记
unsigned char* areas; /// 每个多边形的区域
int nverts; /// 顶点数量
int npolys; /// 多边形数量
int maxpolys; /// 已申请的最大多边形数量
int nvp; /// 每个多边形的最大顶点数量
float bmin[3]; /// 同 rcContourSet
float bmax[3]; /// 同 rcContourSet
float cs; /// 同 rcContourSet
float ch; /// 同 rcContourSet
int borderSize; /// 同 rcConfig::borderSize
float maxEdgeError; /// 同 rcContourSet::maxError
...
};
- 建立过程通过
rcBuildPolyMesh方法实现,其代码如下:
// Recast/Source/RecastMesh.cpp
...
bool rcBuildPolyMesh(rcContext* ctx, const rcContourSet& cset, const int nvp, rcPolyMesh& mesh)
{
rcAssert(ctx);
rcScopedTimer timer(ctx, RC_TIMER_BUILD_POLYMESH);
rcVcopy(mesh.bmin, cset.bmin);
rcVcopy(mesh.bmax, cset.bmax);
mesh.cs = cset.cs;
mesh.ch = cset.ch;
mesh.borderSize = cset.borderSize;
mesh.maxEdgeError = cset.maxError;
int maxVertices = 0;
int maxTris = 0;
int maxVertsPerCont = 0;
for (int i = 0; i < cset.nconts; ++i)
{
// Skip null contours.
if (cset.conts[i].nverts < 3) continue;
maxVertices += cset.conts[i].nverts;
maxTris += cset.conts[i].nverts - 2;
maxVertsPerCont = rcMax(maxVertsPerCont, cset.conts[i].nverts);
}
if (maxVertices >= 0xfffe)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Too many vertices %d.", maxVertices);
return false;
}
rcScopedDelete<unsigned char> vflags((unsigned char*)rcAlloc(sizeof(unsigned char)*maxVertices, RC_ALLOC_TEMP));
if (!vflags)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Out of memory 'vflags' (%d).", maxVertices);
return false;
}
memset(vflags, 0, maxVertices);
mesh.verts = (unsigned short*)rcAlloc(sizeof(unsigned short)*maxVertices*3, RC_ALLOC_PERM);
if (!mesh.verts)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Out of memory 'mesh.verts' (%d).", maxVertices);
return false;
}
mesh.polys = (unsigned short*)rcAlloc(sizeof(unsigned short)*maxTris*nvp*2, RC_ALLOC_PERM);
if (!mesh.polys)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Out of memory 'mesh.polys' (%d).", maxTris*nvp*2);
return false;
}
mesh.regs = (unsigned short*)rcAlloc(sizeof(unsigned short)*maxTris, RC_ALLOC_PERM);
if (!mesh.regs)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Out of memory 'mesh.regs' (%d).", maxTris);
return false;
}
mesh.areas = (unsigned char*)rcAlloc(sizeof(unsigned char)*maxTris, RC_ALLOC_PERM);
if (!mesh.areas)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Out of memory 'mesh.areas' (%d).", maxTris);
return false;
}
mesh.nverts = 0;
mesh.npolys = 0;
mesh.nvp = nvp;
mesh.maxpolys = maxTris;
memset(mesh.verts, 0, sizeof(unsigned short)*maxVertices*3);
memset(mesh.polys, 0xff, sizeof(unsigned short)*maxTris*nvp*2);
memset(mesh.regs, 0, sizeof(unsigned short)*maxTris);
memset(mesh.areas, 0, sizeof(unsigned char)*maxTris);
rcScopedDelete<int> nextVert((int*)rcAlloc(sizeof(int)*maxVertices, RC_ALLOC_TEMP));
if (!nextVert)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Out of memory 'nextVert' (%d).", maxVertices);
return false;
}
memset(nextVert, 0, sizeof(int)*maxVertices);
rcScopedDelete<int> firstVert((int*)rcAlloc(sizeof(int)*VERTEX_BUCKET_COUNT, RC_ALLOC_TEMP));
if (!firstVert)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Out of memory 'firstVert' (%d).", VERTEX_BUCKET_COUNT);
return false;
}
for (int i = 0; i < VERTEX_BUCKET_COUNT; ++i)
firstVert[i] = -1;
rcScopedDelete<int> indices((int*)rcAlloc(sizeof(int)*maxVertsPerCont, RC_ALLOC_TEMP));
if (!indices)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Out of memory 'indices' (%d).", maxVertsPerCont);
return false;
}
rcScopedDelete<int> tris((int*)rcAlloc(sizeof(int)*maxVertsPerCont*3, RC_ALLOC_TEMP));
if (!tris)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Out of memory 'tris' (%d).", maxVertsPerCont*3);
return false;
}
rcScopedDelete<unsigned short> polys((unsigned short*)rcAlloc(sizeof(unsigned short)*(maxVertsPerCont+1)*nvp, RC_ALLOC_TEMP));
if (!polys)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Out of memory 'polys' (%d).", maxVertsPerCont*nvp);
return false;
}
unsigned short* tmpPoly = &polys[maxVertsPerCont*nvp];
for (int i = 0; i < cset.nconts; ++i)
{
rcContour& cont = cset.conts[i];
// Skip null contours.
if (cont.nverts < 3)
continue;
// Triangulate contour
for (int j = 0; j < cont.nverts; ++j)
indices[j] = j;
int ntris = triangulate(cont.nverts, cont.verts, &indices[0], &tris[0]);
if (ntris <= 0)
{
// Bad triangulation, should not happen.
/* printf("\tconst float bmin[3] = {%ff,%ff,%ff};\n", cset.bmin[0], cset.bmin[1], cset.bmin[2]);
printf("\tconst float cs = %ff;\n", cset.cs);
printf("\tconst float ch = %ff;\n", cset.ch);
printf("\tconst int verts[] = {\n");
for (int k = 0; k < cont.nverts; ++k)
{
const int* v = &cont.verts[k*4];
printf("\t\t%d,%d,%d,%d,\n", v[0], v[1], v[2], v[3]);
}
printf("\t};\n\tconst int nverts = sizeof(verts)/(sizeof(int)*4);\n");*/
ctx->log(RC_LOG_WARNING, "rcBuildPolyMesh: Bad triangulation Contour %d.", i);
ntris = -ntris;
}
// Add and merge vertices.
for (int j = 0; j < cont.nverts; ++j)
{
const int* v = &cont.verts[j*4];
indices[j] = addVertex((unsigned short)v[0], (unsigned short)v[1], (unsigned short)v[2],
mesh.verts, firstVert, nextVert, mesh.nverts);
if (v[3] & RC_BORDER_VERTEX)
{
// This vertex should be removed.
vflags[indices[j]] = 1;
}
}
// Build initial polygons.
int npolys = 0;
memset(polys, 0xff, maxVertsPerCont*nvp*sizeof(unsigned short));
for (int j = 0; j < ntris; ++j)
{
int* t = &tris[j*3];
if (t[0] != t[1] && t[0] != t[2] && t[1] != t[2])
{
polys[npolys*nvp+0] = (unsigned short)indices[t[0]];
polys[npolys*nvp+1] = (unsigned short)indices[t[1]];
polys[npolys*nvp+2] = (unsigned short)indices[t[2]];
npolys++;
}
}
if (!npolys)
continue;
// Merge polygons.
if (nvp > 3)
{
for(;;)
{
// Find best polygons to merge.
int bestMergeVal = 0;
int bestPa = 0, bestPb = 0, bestEa = 0, bestEb = 0;
for (int j = 0; j < npolys-1; ++j)
{
unsigned short* pj = &polys[j*nvp];
for (int k = j+1; k < npolys; ++k)
{
unsigned short* pk = &polys[k*nvp];
int ea, eb;
int v = getPolyMergeValue(pj, pk, mesh.verts, ea, eb, nvp);
if (v > bestMergeVal)
{
bestMergeVal = v;
bestPa = j;
bestPb = k;
bestEa = ea;
bestEb = eb;
}
}
}
if (bestMergeVal > 0)
{
// Found best, merge.
unsigned short* pa = &polys[bestPa*nvp];
unsigned short* pb = &polys[bestPb*nvp];
mergePolyVerts(pa, pb, bestEa, bestEb, tmpPoly, nvp);
unsigned short* lastPoly = &polys[(npolys-1)*nvp];
if (pb != lastPoly)
memcpy(pb, lastPoly, sizeof(unsigned short)*nvp);
npolys--;
}
else
{
// Could not merge any polygons, stop.
break;
}
}
}
// Store polygons.
for (int j = 0; j < npolys; ++j)
{
unsigned short* p = &mesh.polys[mesh.npolys*nvp*2];
unsigned short* q = &polys[j*nvp];
for (int k = 0; k < nvp; ++k)
p[k] = q[k];
mesh.regs[mesh.npolys] = cont.reg;
mesh.areas[mesh.npolys] = cont.area;
mesh.npolys++;
if (mesh.npolys > maxTris)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Too many polygons %d (max:%d).", mesh.npolys, maxTris);
return false;
}
}
}
// Remove edge vertices.
for (int i = 0; i < mesh.nverts; ++i)
{
if (vflags[i])
{
if (!canRemoveVertex(ctx, mesh, (unsigned short)i))
continue;
if (!removeVertex(ctx, mesh, (unsigned short)i, maxTris))
{
// Failed to remove vertex
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Failed to remove edge vertex %d.", i);
return false;
}
// Remove vertex
// Note: mesh.nverts is already decremented inside removeVertex()!
// Fixup vertex flags
for (int j = i; j < mesh.nverts; ++j)
vflags[j] = vflags[j+1];
--i;
}
}
// Calculate adjacency.
if (!buildMeshAdjacency(mesh.polys, mesh.npolys, mesh.nverts, nvp))
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Adjacency failed.");
return false;
}
// Find portal edges
if (mesh.borderSize > 0)
{
const int w = cset.width;
const int h = cset.height;
for (int i = 0; i < mesh.npolys; ++i)
{
unsigned short* p = &mesh.polys[i*2*nvp];
for (int j = 0; j < nvp; ++j)
{
if (p[j] == RC_MESH_NULL_IDX) break;
// Skip connected edges.
if (p[nvp+j] != RC_MESH_NULL_IDX)
continue;
int nj = j+1;
if (nj >= nvp || p[nj] == RC_MESH_NULL_IDX) nj = 0;
const unsigned short* va = &mesh.verts[p[j]*3];
const unsigned short* vb = &mesh.verts[p[nj]*3];
if ((int)va[0] == 0 && (int)vb[0] == 0)
p[nvp+j] = 0x8000 | 0;
else if ((int)va[2] == h && (int)vb[2] == h)
p[nvp+j] = 0x8000 | 1;
else if ((int)va[0] == w && (int)vb[0] == w)
p[nvp+j] = 0x8000 | 2;
else if ((int)va[2] == 0 && (int)vb[2] == 0)
p[nvp+j] = 0x8000 | 3;
}
}
}
// Just allocate the mesh flags array. The user is resposible to fill it.
mesh.flags = (unsigned short*)rcAlloc(sizeof(unsigned short)*mesh.npolys, RC_ALLOC_PERM);
if (!mesh.flags)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: Out of memory 'mesh.flags' (%d).", mesh.npolys);
return false;
}
memset(mesh.flags, 0, sizeof(unsigned short) * mesh.npolys);
if (mesh.nverts > 0xffff)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: The resulting mesh has too many vertices %d (max %d). Data can be corrupted.", mesh.nverts, 0xffff);
}
if (mesh.npolys > 0xffff)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMesh: The resulting mesh has too many polygons %d (max %d). Data can be corrupted.", mesh.npolys, 0xffff);
}
return true;
}
...
rcBuildPolyMesh的主要步骤如下:- 初始化
rcPolyMesh结构mesh对象,用于存储网格信息,其中mesh.polys的值初始化为0xff(后续判断有效的点是判断值是否为RC_MESH_NULL_IDX,即0xffff,所以这里应该初始化需要设置成0xffff?)。 - 遍历
cset中的轮廓处理。- 初始化顶点索引
indices,通过triangulate方法将轮廓划分成三角形,存储到tris中。 - 遍历轮廓的每个顶点,通过
addVertex方法去除重复顶点(x、z 坐标相同,y 坐标差值在 2 以内),重新生成顶点索引,更新到indices中,并将顶点坐标记录到mesh.verts中。同时,对处在borderSize范围内的顶点标记到vflags中。 - 将
indices每个三角形的顶点索引存储到临时数组polys中。 - 如果每个多边形的最大顶点数
nvp大于 3,则进行多边形合并。- 遍历
polys中每两个多边形,通过getPolyMergeValue方法找到所有具有公共边的多边形组合,取其中公共边最长的多边形组合,通过mergePolyVerts方法,按照顶点顺序,从各自的公共边终点起,依次加入到新的多边形顶点数组中。 - 直到没有多边形能进行合并时,结束合并。
- 遍历
- 将多边形数据
polys存储到mesh.polys中,且记录每个多边形所属的region和area。
- 初始化顶点索引
- 遍历
mesh.verts中的每个顶点,如果该顶点标记在vflags中,则通过canRemoveVertex方法检查该顶点能否移除,如果能移除则通过removeVertex方法移除。 - 通过
buildMeshAdjacency方法,计算并记录多边形的邻居信息。 - 如果
borderSize大于 0,则检查所有多边形的非共享边,根据边的 x 、z 坐标,将入口边界信息记录到mesh.polys[nvp + j]中(j 为边的起始点索引)。- 如果边的 x 坐标都为 0 ,即为左入口边界,则
mesh.polys[nvp + j] = 0x8000。 - 如果边的 z 坐标都为
cset.height,即为上入口边界,则mesh.polys[nvp + j] = 0x8001。 - 如果边的 x 坐标都为
cset.width,即为右入口边界,则mesh.polys[nvp + j] = 0x8002。 - 如果边的 z 坐标都为 0 ,即为下入口边界,则
mesh.polys[nvp + j] = 0x8003。
- 如果边的 x 坐标都为 0 ,即为左入口边界,则
- 初始化
mesh.flags数组,大小为mesh.npolys,用于后续标记使用。
- 初始化
将轮廓点划分成三角形
triangulate方法的实现如下:
// Recase/Source/RecastMesh.cpp
...
static int triangulate(int n, const int* verts, int* indices, int* tris)
{
int ntris = 0;
int* dst = tris;
// The last bit of the index is used to indicate if the vertex can be removed.
for (int i = 0; i < n; i++)
{
int i1 = next(i, n);
int i2 = next(i1, n);
if (diagonal(i, i2, n, verts, indices))
indices[i1] |= 0x80000000;
}
while (n > 3)
{
int minLen = -1;
int mini = -1;
for (int i = 0; i < n; i++)
{
int i1 = next(i, n);
if (indices[i1] & 0x80000000)
{
const int* p0 = &verts[(indices[i] & 0x0fffffff) * 4];
const int* p2 = &verts[(indices[next(i1, n)] & 0x0fffffff) * 4];
int dx = p2[0] - p0[0];
int dy = p2[2] - p0[2];
int len = dx*dx + dy*dy;
if (minLen < 0 || len < minLen)
{
minLen = len;
mini = i;
}
}
}
if (mini == -1)
{
// We might get here because the contour has overlapping segments, like this:
//
// A o-o=====o---o B
// / |C D| \.
// o o o o
// : : : :
// We'll try to recover by loosing up the inCone test a bit so that a diagonal
// like A-B or C-D can be found and we can continue.
minLen = -1;
mini = -1;
for (int i = 0; i < n; i++)
{
int i1 = next(i, n);
int i2 = next(i1, n);
if (diagonalLoose(i, i2, n, verts, indices))
{
const int* p0 = &verts[(indices[i] & 0x0fffffff) * 4];
const int* p2 = &verts[(indices[next(i2, n)] & 0x0fffffff) * 4];
int dx = p2[0] - p0[0];
int dy = p2[2] - p0[2];
int len = dx*dx + dy*dy;
if (minLen < 0 || len < minLen)
{
minLen = len;
mini = i;
}
}
}
if (mini == -1)
{
// The contour is messed up. This sometimes happens
// if the contour simplification is too aggressive.
return -ntris;
}
}
int i = mini;
int i1 = next(i, n);
int i2 = next(i1, n);
*dst++ = indices[i] & 0x0fffffff;
*dst++ = indices[i1] & 0x0fffffff;
*dst++ = indices[i2] & 0x0fffffff;
ntris++;
// Removes P[i1] by copying P[i+1]...P[n-1] left one index.
n--;
for (int k = i1; k < n; k++)
indices[k] = indices[k+1];
if (i1 >= n) i1 = 0;
i = prev(i1,n);
// Update diagonal flags.
if (diagonal(prev(i, n), i1, n, verts, indices))
indices[i] |= 0x80000000;
else
indices[i] &= 0x0fffffff;
if (diagonal(i, next(i1, n), n, verts, indices))
indices[i1] |= 0x80000000;
else
indices[i1] &= 0x0fffffff;
}
// Append the remaining triangle.
*dst++ = indices[0] & 0x0fffffff;
*dst++ = indices[1] & 0x0fffffff;
*dst++ = indices[2] & 0x0fffffff;
ntris++;
return ntris;
}
...
- 将轮廓点划分成三角形的步骤如下:
- 遍历每个顶点
i,通过diagonal方法,检查顶点i和i + 2组成的线段的包围盒是否和轮廓不包含这两个点的边的包围盒相交,如果不相交,表示该线段可以划分三角形,标记indices[i + 1]的最高位为 1。diagonal方法最终也是通过inCone和intersect方法实现。
- 当轮廓顶点数量超过 3 时,即可以划分成多个三角形,则进行迭代检查处理。
- 遍历每个顶点
i,如果indices[i + 1]已经标记,则计算i和i + 2组成的线段长度,记录所有长度中的最小值及对应的顶点索引。 - 如果顶点都没有标记,则通过
diagonalLoose方法,再次遍历每个顶点i检查相交情况。如果不相交,同样计算i和i + 2组成的线段长度,记录所有长度中的最小值及对应的顶点索引。如果还是没有找到不相交的对角线,则当前轮廓无法再划分三角形,返回-ntris。diagonalLoose方法是通过inConeLoose和intersectProp方法实现,降低了对划分三角形的对角线要求,即。其中,inConeLoose检查点是否在角度范围内时,增加了三个点共线的情况,intersectProp方法只检查线段直接相交的情况。
- 将长度最小值对应的顶点索引
i及其后续两个顶点i + 1和i + 2,依次加入到tris中,作为一个划分的三角形,并从轮廓点中移除i + 1顶点。 - 对顶点
i - 1和i,通过diagonal方法,重新检查相交情况进行标记。 - 继续进行迭代划分,直到不能再划分为止。
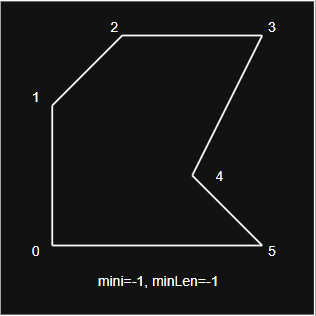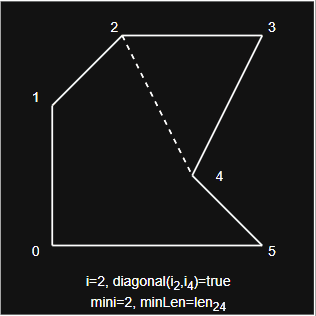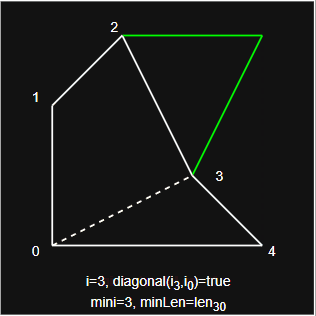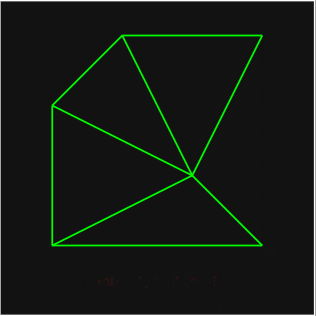
- 遍历每个顶点
- 遍历每个顶点
查找多边形公共边
getPolyMergeValue的实现如下:
// Recast/Source/RecastMesh.cpp
...
static int getPolyMergeValue(unsigned short* pa, unsigned short* pb,
const unsigned short* verts, int& ea, int& eb,
const int nvp)
{
const int na = countPolyVerts(pa, nvp);
const int nb = countPolyVerts(pb, nvp);
// If the merged polygon would be too big, do not merge.
if (na+nb-2 > nvp)
return -1;
// Check if the polygons share an edge.
ea = -1;
eb = -1;
for (int i = 0; i < na; ++i)
{
unsigned short va0 = pa[i];
unsigned short va1 = pa[(i+1) % na];
if (va0 > va1)
rcSwap(va0, va1);
for (int j = 0; j < nb; ++j)
{
unsigned short vb0 = pb[j];
unsigned short vb1 = pb[(j+1) % nb];
if (vb0 > vb1)
rcSwap(vb0, vb1);
if (va0 == vb0 && va1 == vb1)
{
ea = i;
eb = j;
break;
}
}
}
// No common edge, cannot merge.
if (ea == -1 || eb == -1)
return -1;
// Check to see if the merged polygon would be convex.
unsigned short va, vb, vc;
va = pa[(ea+na-1) % na];
vb = pa[ea];
vc = pb[(eb+2) % nb];
if (!uleft(&verts[va*3], &verts[vb*3], &verts[vc*3]))
return -1;
va = pb[(eb+nb-1) % nb];
vb = pb[eb];
vc = pa[(ea+2) % na];
if (!uleft(&verts[va*3], &verts[vb*3], &verts[vc*3]))
return -1;
va = pa[ea];
vb = pa[(ea+1)%na];
int dx = (int)verts[va*3+0] - (int)verts[vb*3+0];
int dy = (int)verts[va*3+2] - (int)verts[vb*3+2];
return dx*dx + dy*dy;
}
...
getPolyMergeValue查找公共边的步骤如下:- 检查两个多边形合并后的顶点数量,如果超过
nvp则不能合并。 - 遍历第一个多边形的每条边,从第二个多边形中查找是否有相同的边,找到则记录边对应的顶点索引。
- 检查公共边合并后新的两个角是否为凸角,如果是则计算公共边距离平方返回,表示该公共边可以合并。检查方式为:
- 检查第二个多边形中公共边的下一个顶点,是否在第一个多边形公共边的上一个顶点及第一个顶点组成的向量右侧。
- 检查第一个多边形中公共边的下一个顶点,是否在第二个多边形公共边的上一个顶点及第一个顶点组成的向量右侧。
- 检查两个多边形合并后的顶点数量,如果超过
移除边界顶点
- 合并完成后,对于处在
borderSize范围内的顶点,通过canRemoveVertex检查是否能移除,其实现如下:
// Recast/Source/RecastMesh.cpp
...
static bool canRemoveVertex(rcContext* ctx, rcPolyMesh& mesh, const unsigned short rem)
{
const int nvp = mesh.nvp;
// Count number of polygons to remove.
int numTouchedVerts = 0;
int numRemainingEdges = 0;
for (int i = 0; i < mesh.npolys; ++i)
{
unsigned short* p = &mesh.polys[i*nvp*2];
const int nv = countPolyVerts(p, nvp);
int numRemoved = 0;
int numVerts = 0;
for (int j = 0; j < nv; ++j)
{
if (p[j] == rem)
{
numTouchedVerts++;
numRemoved++;
}
numVerts++;
}
if (numRemoved)
{
numRemainingEdges += numVerts-(numRemoved+1);
}
}
// There would be too few edges remaining to create a polygon.
// This can happen for example when a tip of a triangle is marked
// as deletion, but there are no other polys that share the vertex.
// In this case, the vertex should not be removed.
if (numRemainingEdges <= 2)
return false;
// Find edges which share the removed vertex.
const int maxEdges = numTouchedVerts*2;
int nedges = 0;
rcScopedDelete<int> edges((int*)rcAlloc(sizeof(int)*maxEdges*3, RC_ALLOC_TEMP));
if (!edges)
{
ctx->log(RC_LOG_WARNING, "canRemoveVertex: Out of memory 'edges' (%d).", maxEdges*3);
return false;
}
for (int i = 0; i < mesh.npolys; ++i)
{
unsigned short* p = &mesh.polys[i*nvp*2];
const int nv = countPolyVerts(p, nvp);
// Collect edges which touches the removed vertex.
for (int j = 0, k = nv-1; j < nv; k = j++)
{
if (p[j] == rem || p[k] == rem)
{
// Arrange edge so that a=rem.
int a = p[j], b = p[k];
if (b == rem)
rcSwap(a,b);
// Check if the edge exists
bool exists = false;
for (int m = 0; m < nedges; ++m)
{
int* e = &edges[m*3];
if (e[1] == b)
{
// Exists, increment vertex share count.
e[2]++;
exists = true;
}
}
// Add new edge.
if (!exists)
{
int* e = &edges[nedges*3];
e[0] = a;
e[1] = b;
e[2] = 1;
nedges++;
}
}
}
}
// There should be no more than 2 open edges.
// This catches the case that two non-adjacent polygons
// share the removed vertex. In that case, do not remove the vertex.
int numOpenEdges = 0;
for (int i = 0; i < nedges; ++i)
{
if (edges[i*3+2] < 2)
numOpenEdges++;
}
if (numOpenEdges > 2)
return false;
return true;
}
...
canRemoveVertex的检查过程如下:- 遍历
mesh中的所有多边形,统计顶点总数和包含待移除的顶点数量,计算移除顶点后的剩余边数,确保不能小于 2。 - 遍历
mesh的每个多边形,记录包含待移除顶点的边的出现次数,如果出现次数大于 2,则该边为公共边,否则为开放边。 - 检查包含待移除顶点的所有边,如果出现超过 2 条开放边,则表示该顶点移除会出现多个开口,会破坏多边形结构,因此不能移除。
- 遍历
- 移除顶点的方法
removeVertex的实现如下:
// Recast/Source/RecastMesh.cpp
...
static bool removeVertex(rcContext* ctx, rcPolyMesh& mesh, const unsigned short rem, const int maxTris)
{
const int nvp = mesh.nvp;
// Count number of polygons to remove.
int numRemovedVerts = 0;
for (int i = 0; i < mesh.npolys; ++i)
{
unsigned short* p = &mesh.polys[i*nvp*2];
const int nv = countPolyVerts(p, nvp);
for (int j = 0; j < nv; ++j)
{
if (p[j] == rem)
numRemovedVerts++;
}
}
int nedges = 0;
rcScopedDelete<int> edges((int*)rcAlloc(sizeof(int)*numRemovedVerts*nvp*4, RC_ALLOC_TEMP));
if (!edges)
{
ctx->log(RC_LOG_WARNING, "removeVertex: Out of memory 'edges' (%d).", numRemovedVerts*nvp*4);
return false;
}
int nhole = 0;
rcScopedDelete<int> hole((int*)rcAlloc(sizeof(int)*numRemovedVerts*nvp, RC_ALLOC_TEMP));
if (!hole)
{
ctx->log(RC_LOG_WARNING, "removeVertex: Out of memory 'hole' (%d).", numRemovedVerts*nvp);
return false;
}
int nhreg = 0;
rcScopedDelete<int> hreg((int*)rcAlloc(sizeof(int)*numRemovedVerts*nvp, RC_ALLOC_TEMP));
if (!hreg)
{
ctx->log(RC_LOG_WARNING, "removeVertex: Out of memory 'hreg' (%d).", numRemovedVerts*nvp);
return false;
}
int nharea = 0;
rcScopedDelete<int> harea((int*)rcAlloc(sizeof(int)*numRemovedVerts*nvp, RC_ALLOC_TEMP));
if (!harea)
{
ctx->log(RC_LOG_WARNING, "removeVertex: Out of memory 'harea' (%d).", numRemovedVerts*nvp);
return false;
}
for (int i = 0; i < mesh.npolys; ++i)
{
unsigned short* p = &mesh.polys[i*nvp*2];
const int nv = countPolyVerts(p, nvp);
bool hasRem = false;
for (int j = 0; j < nv; ++j)
if (p[j] == rem) hasRem = true;
if (hasRem)
{
// Collect edges which does not touch the removed vertex.
for (int j = 0, k = nv-1; j < nv; k = j++)
{
if (p[j] != rem && p[k] != rem)
{
int* e = &edges[nedges*4];
e[0] = p[k];
e[1] = p[j];
e[2] = mesh.regs[i];
e[3] = mesh.areas[i];
nedges++;
}
}
// Remove the polygon.
unsigned short* p2 = &mesh.polys[(mesh.npolys-1)*nvp*2];
if (p != p2)
memcpy(p,p2,sizeof(unsigned short)*nvp);
memset(p+nvp,0xff,sizeof(unsigned short)*nvp);
mesh.regs[i] = mesh.regs[mesh.npolys-1];
mesh.areas[i] = mesh.areas[mesh.npolys-1];
mesh.npolys--;
--i;
}
}
// Remove vertex.
for (int i = (int)rem; i < mesh.nverts - 1; ++i)
{
mesh.verts[i*3+0] = mesh.verts[(i+1)*3+0];
mesh.verts[i*3+1] = mesh.verts[(i+1)*3+1];
mesh.verts[i*3+2] = mesh.verts[(i+1)*3+2];
}
mesh.nverts--;
// Adjust indices to match the removed vertex layout.
for (int i = 0; i < mesh.npolys; ++i)
{
unsigned short* p = &mesh.polys[i*nvp*2];
const int nv = countPolyVerts(p, nvp);
for (int j = 0; j < nv; ++j)
if (p[j] > rem) p[j]--;
}
for (int i = 0; i < nedges; ++i)
{
if (edges[i*4+0] > rem) edges[i*4+0]--;
if (edges[i*4+1] > rem) edges[i*4+1]--;
}
if (nedges == 0)
return true;
// Start with one vertex, keep appending connected
// segments to the start and end of the hole.
pushBack(edges[0], hole, nhole);
pushBack(edges[2], hreg, nhreg);
pushBack(edges[3], harea, nharea);
while (nedges)
{
bool match = false;
for (int i = 0; i < nedges; ++i)
{
const int ea = edges[i*4+0];
const int eb = edges[i*4+1];
const int r = edges[i*4+2];
const int a = edges[i*4+3];
bool add = false;
if (hole[0] == eb)
{
// The segment matches the beginning of the hole boundary.
pushFront(ea, hole, nhole);
pushFront(r, hreg, nhreg);
pushFront(a, harea, nharea);
add = true;
}
else if (hole[nhole-1] == ea)
{
// The segment matches the end of the hole boundary.
pushBack(eb, hole, nhole);
pushBack(r, hreg, nhreg);
pushBack(a, harea, nharea);
add = true;
}
if (add)
{
// The edge segment was added, remove it.
edges[i*4+0] = edges[(nedges-1)*4+0];
edges[i*4+1] = edges[(nedges-1)*4+1];
edges[i*4+2] = edges[(nedges-1)*4+2];
edges[i*4+3] = edges[(nedges-1)*4+3];
--nedges;
match = true;
--i;
}
}
if (!match)
break;
}
rcScopedDelete<int> tris((int*)rcAlloc(sizeof(int)*nhole*3, RC_ALLOC_TEMP));
if (!tris)
{
ctx->log(RC_LOG_WARNING, "removeVertex: Out of memory 'tris' (%d).", nhole*3);
return false;
}
rcScopedDelete<int> tverts((int*)rcAlloc(sizeof(int)*nhole*4, RC_ALLOC_TEMP));
if (!tverts)
{
ctx->log(RC_LOG_WARNING, "removeVertex: Out of memory 'tverts' (%d).", nhole*4);
return false;
}
rcScopedDelete<int> thole((int*)rcAlloc(sizeof(int)*nhole, RC_ALLOC_TEMP));
if (!thole)
{
ctx->log(RC_LOG_WARNING, "removeVertex: Out of memory 'thole' (%d).", nhole);
return false;
}
// Generate temp vertex array for triangulation.
for (int i = 0; i < nhole; ++i)
{
const int pi = hole[i];
tverts[i*4+0] = mesh.verts[pi*3+0];
tverts[i*4+1] = mesh.verts[pi*3+1];
tverts[i*4+2] = mesh.verts[pi*3+2];
tverts[i*4+3] = 0;
thole[i] = i;
}
// Triangulate the hole.
int ntris = triangulate(nhole, &tverts[0], &thole[0], tris);
if (ntris < 0)
{
ntris = -ntris;
ctx->log(RC_LOG_WARNING, "removeVertex: triangulate() returned bad results.");
}
// Merge the hole triangles back to polygons.
rcScopedDelete<unsigned short> polys((unsigned short*)rcAlloc(sizeof(unsigned short)*(ntris+1)*nvp, RC_ALLOC_TEMP));
if (!polys)
{
ctx->log(RC_LOG_ERROR, "removeVertex: Out of memory 'polys' (%d).", (ntris+1)*nvp);
return false;
}
rcScopedDelete<unsigned short> pregs((unsigned short*)rcAlloc(sizeof(unsigned short)*ntris, RC_ALLOC_TEMP));
if (!pregs)
{
ctx->log(RC_LOG_ERROR, "removeVertex: Out of memory 'pregs' (%d).", ntris);
return false;
}
rcScopedDelete<unsigned char> pareas((unsigned char*)rcAlloc(sizeof(unsigned char)*ntris, RC_ALLOC_TEMP));
if (!pareas)
{
ctx->log(RC_LOG_ERROR, "removeVertex: Out of memory 'pareas' (%d).", ntris);
return false;
}
unsigned short* tmpPoly = &polys[ntris*nvp];
// Build initial polygons.
int npolys = 0;
memset(polys, 0xff, ntris*nvp*sizeof(unsigned short));
for (int j = 0; j < ntris; ++j)
{
int* t = &tris[j*3];
if (t[0] != t[1] && t[0] != t[2] && t[1] != t[2])
{
polys[npolys*nvp+0] = (unsigned short)hole[t[0]];
polys[npolys*nvp+1] = (unsigned short)hole[t[1]];
polys[npolys*nvp+2] = (unsigned short)hole[t[2]];
// If this polygon covers multiple region types then
// mark it as such
if (hreg[t[0]] != hreg[t[1]] || hreg[t[1]] != hreg[t[2]])
pregs[npolys] = RC_MULTIPLE_REGS;
else
pregs[npolys] = (unsigned short)hreg[t[0]];
pareas[npolys] = (unsigned char)harea[t[0]];
npolys++;
}
}
if (!npolys)
return true;
// Merge polygons.
if (nvp > 3)
{
for (;;)
{
// Find best polygons to merge.
int bestMergeVal = 0;
int bestPa = 0, bestPb = 0, bestEa = 0, bestEb = 0;
for (int j = 0; j < npolys-1; ++j)
{
unsigned short* pj = &polys[j*nvp];
for (int k = j+1; k < npolys; ++k)
{
unsigned short* pk = &polys[k*nvp];
int ea, eb;
int v = getPolyMergeValue(pj, pk, mesh.verts, ea, eb, nvp);
if (v > bestMergeVal)
{
bestMergeVal = v;
bestPa = j;
bestPb = k;
bestEa = ea;
bestEb = eb;
}
}
}
if (bestMergeVal > 0)
{
// Found best, merge.
unsigned short* pa = &polys[bestPa*nvp];
unsigned short* pb = &polys[bestPb*nvp];
mergePolyVerts(pa, pb, bestEa, bestEb, tmpPoly, nvp);
if (pregs[bestPa] != pregs[bestPb])
pregs[bestPa] = RC_MULTIPLE_REGS;
unsigned short* last = &polys[(npolys-1)*nvp];
if (pb != last)
memcpy(pb, last, sizeof(unsigned short)*nvp);
pregs[bestPb] = pregs[npolys-1];
pareas[bestPb] = pareas[npolys-1];
npolys--;
}
else
{
// Could not merge any polygons, stop.
break;
}
}
}
// Store polygons.
for (int i = 0; i < npolys; ++i)
{
if (mesh.npolys >= maxTris) break;
unsigned short* p = &mesh.polys[mesh.npolys*nvp*2];
memset(p,0xff,sizeof(unsigned short)*nvp*2);
for (int j = 0; j < nvp; ++j)
p[j] = polys[i*nvp+j];
mesh.regs[mesh.npolys] = pregs[i];
mesh.areas[mesh.npolys] = pareas[i];
mesh.npolys++;
if (mesh.npolys > maxTris)
{
ctx->log(RC_LOG_ERROR, "removeVertex: Too many polygons %d (max:%d).", mesh.npolys, maxTris);
return false;
}
}
return true;
}
...
removeVertex移除的主要步骤如下:- 遍历
mesh的所有多边形,将所有包含待移除顶点的边记录到edges中,并将该多边形从mesh.polys中移除。 - 将目标顶点从
mesh的verts中移除,且更新mesh.polys和edges中的顶点索引。 - 以
edges的第一条边的两个顶点为左侧点和右侧点,遍历edges中的剩余边,找到和左侧点相邻的边,将其的左侧点作为左侧点,找到和右侧点相邻的边,将其右侧点作为右侧点,最终得到一组重新排序的顶点。 - 将排序后的顶点,通过
triangulate方法划分成三角形。 - 将三角形加入到临时数组
polys中,并记录对应的region和area到pregs和pareas中。如果三角形的region不同,则将pregs中对应的值设置为RC_MULTIPLE_REGS。 - 如果每个多边形的最大顶点数
nvp大于 3,则进行多边形合并。通过getPolyMergeValue方法找到公共边,mergePolyVerts方法进行合并。如果两个多边形的region不同,则合并后的多边形的region设置为RC_MULTIPLE_REGS。 - 将合并后的多边形
polys加入到mesh.polys中,同时更新mesh.regs和mesh.areas。
- 遍历
计算多边形邻居
- 计算多边形邻居时,使用了
rcEdge记录边的信息,其结构如下:
// Recast/Source/RecastMesh.cpp
...
struct rcEdge
{
unsigned short vert[2]; /// 边的两个顶点的索引
unsigned short polyEdge[2]; /// 如果边的起始点索引比终点小,则 polyEdge[0] 为起始点在当前多边形中的第几个顶点。如果此时边为公共边,则 polyEdge[1] 为终点在邻居多边形中的第几个顶点
unsigned short poly[2]; /// 两个顶点各自对应的多边形索引
};
...
buildMeshAdjacency的实现如下:
// Recast/Source/RecastMesh.cpp
...
static bool buildMeshAdjacency(unsigned short* polys, const int npolys,
const int nverts, const int vertsPerPoly)
{
// Based on code by Eric Lengyel from:
// https://web.archive.org/web/20080704083314/http://www.terathon.com/code/edges.php
int maxEdgeCount = npolys*vertsPerPoly;
unsigned short* firstEdge = (unsigned short*)rcAlloc(sizeof(unsigned short)*(nverts + maxEdgeCount), RC_ALLOC_TEMP);
if (!firstEdge)
return false;
unsigned short* nextEdge = firstEdge + nverts;
int edgeCount = 0;
rcEdge* edges = (rcEdge*)rcAlloc(sizeof(rcEdge)*maxEdgeCount, RC_ALLOC_TEMP);
if (!edges)
{
rcFree(firstEdge);
return false;
}
for (int i = 0; i < nverts; i++)
firstEdge[i] = RC_MESH_NULL_IDX;
for (int i = 0; i < npolys; ++i)
{
unsigned short* t = &polys[i*vertsPerPoly*2];
for (int j = 0; j < vertsPerPoly; ++j)
{
if (t[j] == RC_MESH_NULL_IDX) break;
unsigned short v0 = t[j];
unsigned short v1 = (j+1 >= vertsPerPoly || t[j+1] == RC_MESH_NULL_IDX) ? t[0] : t[j+1];
if (v0 < v1)
{
rcEdge& edge = edges[edgeCount];
edge.vert[0] = v0;
edge.vert[1] = v1;
edge.poly[0] = (unsigned short)i;
edge.polyEdge[0] = (unsigned short)j;
edge.poly[1] = (unsigned short)i;
edge.polyEdge[1] = 0;
// Insert edge
nextEdge[edgeCount] = firstEdge[v0];
firstEdge[v0] = (unsigned short)edgeCount;
edgeCount++;
}
}
}
for (int i = 0; i < npolys; ++i)
{
unsigned short* t = &polys[i*vertsPerPoly*2];
for (int j = 0; j < vertsPerPoly; ++j)
{
if (t[j] == RC_MESH_NULL_IDX) break;
unsigned short v0 = t[j];
unsigned short v1 = (j+1 >= vertsPerPoly || t[j+1] == RC_MESH_NULL_IDX) ? t[0] : t[j+1];
if (v0 > v1)
{
for (unsigned short e = firstEdge[v1]; e != RC_MESH_NULL_IDX; e = nextEdge[e])
{
rcEdge& edge = edges[e];
if (edge.vert[1] == v0 && edge.poly[0] == edge.poly[1])
{
edge.poly[1] = (unsigned short)i;
edge.polyEdge[1] = (unsigned short)j;
break;
}
}
}
}
}
// Store adjacency
for (int i = 0; i < edgeCount; ++i)
{
const rcEdge& e = edges[i];
if (e.poly[0] != e.poly[1])
{
unsigned short* p0 = &polys[e.poly[0]*vertsPerPoly*2];
unsigned short* p1 = &polys[e.poly[1]*vertsPerPoly*2];
p0[vertsPerPoly + e.polyEdge[0]] = e.poly[1];
p1[vertsPerPoly + e.polyEdge[1]] = e.poly[0];
}
}
rcFree(firstEdge);
rcFree(edges);
return true;
}
...
buildMeshAdjacency的主要步骤如下:- 对每一个多边形,遍历其所有顶点,获取每个顶点为起始点的边,将起始点比终点索引小的边记录到
edges中。edge.vert[0]设置为起始顶点的索引,edge.vert[1]设置为终点顶点的索引。edge.poly[0]和edge.poly[1]都设置为当前多边形的索引。edge.polyEdge[0]设置为起始点在当前多边形中的第几个顶点,edge.polyEdge[1]设置为 0 。- 将具有相同起始点的边通过
nextEdge连接起来。
- 对每一个多边形,遍历其所有顶点,获取每个顶点为起始点的边,对起始点比终点索引大的边进行检查,如果该边在
edges中,则更新边的信息。edge.poly[1]设置为当前多边形的索引,即为edge.poly[0]的邻居多边形。edge.polyEdge[1]设置为edge.vert[1]在邻居多边形中的第几个顶点。
- 遍历
edges中的边,如果两个多边形的索引不同,则该边为公共边,需要将相邻信息记录到各自所属的多边形中,即mesh.polys中,其中mesh.polys[i * nvp * 2 + j]为多边形i的第j个顶点,则邻居信息需要记录在mesh.polys[i * nvp * 2 + nvp + j]中,mesh.polys[edge.poly[0] * nvp * 2 + nvp + edge.polyEdge[0]]设置为edge.poly[1],即edge.poly[0]的第edge.polyEdge[0]个顶点的邻居多边形为edge.poly[1]。mesh.polys[edge.poly[1] * nvp * 2 + nvp + edge.polyEdge[1]]设置为edge.poly[0],即edge.poly[1]的第edge.polyEdge[1]个顶点的邻居多边形为edge.poly[0]。
- 对每一个多边形,遍历其所有顶点,获取每个顶点为起始点的边,将起始点比终点索引小的边记录到
七、创建细节网格
- 创建细节网格过程,使用
rcPolyMeshDetail结构保存细节网格数据,其定义如下:
// Recast/Include/Recast.h
struct rcPolyMeshDetail
{
...
unsigned int* meshes; /// 所有子网格数据,长度为 4 * nmeshes,每个多边形对应一个子网格,占 4 个数据,分别为:之前所有子网格的总顶点数、当前子网格顶点数、之前所有子网格的三角面总数、当前子网格的三角面数
float* verts; /// 所有子网格顶点数据,长度为 3 * nverts
unsigned char* tris; /// 所有子网格的三角面顶点索引,长度为 3 * ntris,每个三角面占 4 个数据,分别为:三个顶点的索引、三条边是否为初始网格边的标记
int nmeshes; /// 子网格数量
int nverts; /// 子网格总顶点数量
int ntris; /// 子网格总三角面数量
...
};
- 创建细节网格使用
rcBuildPolyMeshDetail方法,其实现如下:
// Recast/Source/RecastMeshDetail.cpp
...
bool rcBuildPolyMeshDetail(rcContext* ctx, const rcPolyMesh& mesh, const rcCompactHeightfield& chf,
const float sampleDist, const float sampleMaxError,
rcPolyMeshDetail& dmesh)
{
rcAssert(ctx);
rcScopedTimer timer(ctx, RC_TIMER_BUILD_POLYMESHDETAIL);
if (mesh.nverts == 0 || mesh.npolys == 0)
return true;
const int nvp = mesh.nvp;
const float cs = mesh.cs;
const float ch = mesh.ch;
const float* orig = mesh.bmin;
const int borderSize = mesh.borderSize;
const int heightSearchRadius = rcMax(1, (int)ceilf(mesh.maxEdgeError));
rcTempVector<int> edges(64);
rcTempVector<int> tris(512);
rcTempVector<int> arr(512);
rcTempVector<int> samples(512);
float verts[256*3];
rcHeightPatch hp;
int nPolyVerts = 0;
int maxhw = 0, maxhh = 0;
rcScopedDelete<int> bounds((int*)rcAlloc(sizeof(int)*mesh.npolys*4, RC_ALLOC_TEMP));
if (!bounds)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMeshDetail: Out of memory 'bounds' (%d).", mesh.npolys*4);
return false;
}
rcScopedDelete<float> poly((float*)rcAlloc(sizeof(float)*nvp*3, RC_ALLOC_TEMP));
if (!poly)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMeshDetail: Out of memory 'poly' (%d).", nvp*3);
return false;
}
// Find max size for a polygon area.
for (int i = 0; i < mesh.npolys; ++i)
{
const unsigned short* p = &mesh.polys[i*nvp*2];
int& xmin = bounds[i*4+0];
int& xmax = bounds[i*4+1];
int& ymin = bounds[i*4+2];
int& ymax = bounds[i*4+3];
xmin = chf.width;
xmax = 0;
ymin = chf.height;
ymax = 0;
for (int j = 0; j < nvp; ++j)
{
if(p[j] == RC_MESH_NULL_IDX) break;
const unsigned short* v = &mesh.verts[p[j]*3];
xmin = rcMin(xmin, (int)v[0]);
xmax = rcMax(xmax, (int)v[0]);
ymin = rcMin(ymin, (int)v[2]);
ymax = rcMax(ymax, (int)v[2]);
nPolyVerts++;
}
xmin = rcMax(0,xmin-1);
xmax = rcMin(chf.width,xmax+1);
ymin = rcMax(0,ymin-1);
ymax = rcMin(chf.height,ymax+1);
if (xmin >= xmax || ymin >= ymax) continue;
maxhw = rcMax(maxhw, xmax-xmin);
maxhh = rcMax(maxhh, ymax-ymin);
}
hp.data = (unsigned short*)rcAlloc(sizeof(unsigned short)*maxhw*maxhh, RC_ALLOC_TEMP);
if (!hp.data)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMeshDetail: Out of memory 'hp.data' (%d).", maxhw*maxhh);
return false;
}
dmesh.nmeshes = mesh.npolys;
dmesh.nverts = 0;
dmesh.ntris = 0;
dmesh.meshes = (unsigned int*)rcAlloc(sizeof(unsigned int)*dmesh.nmeshes*4, RC_ALLOC_PERM);
if (!dmesh.meshes)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMeshDetail: Out of memory 'dmesh.meshes' (%d).", dmesh.nmeshes*4);
return false;
}
int vcap = nPolyVerts+nPolyVerts/2;
int tcap = vcap*2;
dmesh.nverts = 0;
dmesh.verts = (float*)rcAlloc(sizeof(float)*vcap*3, RC_ALLOC_PERM);
if (!dmesh.verts)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMeshDetail: Out of memory 'dmesh.verts' (%d).", vcap*3);
return false;
}
dmesh.ntris = 0;
dmesh.tris = (unsigned char*)rcAlloc(sizeof(unsigned char)*tcap*4, RC_ALLOC_PERM);
if (!dmesh.tris)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMeshDetail: Out of memory 'dmesh.tris' (%d).", tcap*4);
return false;
}
for (int i = 0; i < mesh.npolys; ++i)
{
const unsigned short* p = &mesh.polys[i*nvp*2];
// Store polygon vertices for processing.
int npoly = 0;
for (int j = 0; j < nvp; ++j)
{
if(p[j] == RC_MESH_NULL_IDX) break;
const unsigned short* v = &mesh.verts[p[j]*3];
poly[j*3+0] = v[0]*cs;
poly[j*3+1] = v[1]*ch;
poly[j*3+2] = v[2]*cs;
npoly++;
}
// Get the height data from the area of the polygon.
hp.xmin = bounds[i*4+0];
hp.ymin = bounds[i*4+2];
hp.width = bounds[i*4+1]-bounds[i*4+0];
hp.height = bounds[i*4+3]-bounds[i*4+2];
getHeightData(ctx, chf, p, npoly, mesh.verts, borderSize, hp, arr, mesh.regs[i]);
// Build detail mesh.
int nverts = 0;
if (!buildPolyDetail(ctx, poly, npoly,
sampleDist, sampleMaxError,
heightSearchRadius, chf, hp,
verts, nverts, tris,
edges, samples))
{
return false;
}
// Move detail verts to world space.
for (int j = 0; j < nverts; ++j)
{
verts[j*3+0] += orig[0];
verts[j*3+1] += orig[1] + chf.ch; // Is this offset necessary?
verts[j*3+2] += orig[2];
}
// Offset poly too, will be used to flag checking.
for (int j = 0; j < npoly; ++j)
{
poly[j*3+0] += orig[0];
poly[j*3+1] += orig[1];
poly[j*3+2] += orig[2];
}
// Store detail submesh.
const int ntris = static_cast<int>(tris.size()) / 4;
dmesh.meshes[i*4+0] = (unsigned int)dmesh.nverts;
dmesh.meshes[i*4+1] = (unsigned int)nverts;
dmesh.meshes[i*4+2] = (unsigned int)dmesh.ntris;
dmesh.meshes[i*4+3] = (unsigned int)ntris;
// Store vertices, allocate more memory if necessary.
if (dmesh.nverts+nverts > vcap)
{
while (dmesh.nverts+nverts > vcap)
vcap += 256;
float* newv = (float*)rcAlloc(sizeof(float)*vcap*3, RC_ALLOC_PERM);
if (!newv)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMeshDetail: Out of memory 'newv' (%d).", vcap*3);
return false;
}
if (dmesh.nverts)
memcpy(newv, dmesh.verts, sizeof(float)*3*dmesh.nverts);
rcFree(dmesh.verts);
dmesh.verts = newv;
}
for (int j = 0; j < nverts; ++j)
{
dmesh.verts[dmesh.nverts*3+0] = verts[j*3+0];
dmesh.verts[dmesh.nverts*3+1] = verts[j*3+1];
dmesh.verts[dmesh.nverts*3+2] = verts[j*3+2];
dmesh.nverts++;
}
// Store triangles, allocate more memory if necessary.
if (dmesh.ntris+ntris > tcap)
{
while (dmesh.ntris+ntris > tcap)
tcap += 256;
unsigned char* newt = (unsigned char*)rcAlloc(sizeof(unsigned char)*tcap*4, RC_ALLOC_PERM);
if (!newt)
{
ctx->log(RC_LOG_ERROR, "rcBuildPolyMeshDetail: Out of memory 'newt' (%d).", tcap*4);
return false;
}
if (dmesh.ntris)
memcpy(newt, dmesh.tris, sizeof(unsigned char)*4*dmesh.ntris);
rcFree(dmesh.tris);
dmesh.tris = newt;
}
for (int j = 0; j < ntris; ++j)
{
const int* t = &tris[j*4];
dmesh.tris[dmesh.ntris*4+0] = (unsigned char)t[0];
dmesh.tris[dmesh.ntris*4+1] = (unsigned char)t[1];
dmesh.tris[dmesh.ntris*4+2] = (unsigned char)t[2];
dmesh.tris[dmesh.ntris*4+3] = (unsigned char)t[3];
dmesh.ntris++;
}
}
return true;
}
...
- 网格细节的数据存储在
rcPolyMeshDetail结构的dmesh,创建细节网格的主要步骤如下:- 使用
rcPolyMesh网格初始化参数,包括单元格大小mesh.cs、单元格高度mesh.ch、包围盒最小值mesh.bmin、borderSize 大小mesh.borderSize等。 - 遍历网格的每个多边形,找到其中的最大宽高尺寸。
- 创建
tris数组,用于记录细分后的三角面索引信息。 - 创建
verts数组,用于记录细分后的网格顶点坐标。 - 创建
poly数组,用于记录多边形的顶点坐标。 - 遍历网格的每个多边形,对每个多边形进行处理。
- 遍历多边形的每个顶点,获取顶点的单元格坐标,并乘上单元格大小或单元格高度,转化成相对的世界坐标,存入
poly中。- 第二步光栅化后,得到的
span坐标为偏移了高度场的bmin的坐标,而第五步得到轮廓后的顶点坐标,则是在此基础上加上了borderSize的偏移,即最终顶点坐标偏移了rcPolyMesh.bmin(同rcContourSet.bmin)。
- 第二步光栅化后,得到的
- 通过
getHeightData方法,获取多边形的高度信息。 - 通过
buildPolyDetail方法,构建多边形的细节网格,将数据存入tris和verts。 - 将
verts的坐标转化成世界坐标,即加上mesh.bmin的偏移,其中y坐标额外加上chf.ch,即加上单元格的高度。 - 将
poly的坐标转化成世界坐标,即加上mesh.bmin的偏移。 - 设置当前多边形的细节子网格信息。
dmesh.meshes[i*4+0]为之前所有多边形子网格的总顶点数,即当前子网格首个顶点的索引。dmesh.meshes[i*4+1]为当前多边形子网格的顶点数。dmesh.meshes[i*4+2]为之前所有多边形子网格的总三角面数,即当前子网格首个三角面的索引。dmesh.meshes[i*4+3]为当前多边形子网格的三角面数。
- 将
verts加入到dmesh.verts中,并更新dmesh.nverts。 - 将
tris加入到dmesh.tris中,并更新dmesh.ntris。
- 遍历多边形的每个顶点,获取顶点的单元格坐标,并乘上单元格大小或单元格高度,转化成相对的世界坐标,存入
- 使用
生成高度数据
- 生成高度数据方法
getHeightData的实现如下:
// Recast/Source/RecastMeshDetail.cpp
...
static void getHeightData(rcContext* ctx, const rcCompactHeightfield& chf,
const unsigned short* poly, const int npoly,
const unsigned short* verts, const int bs,
rcHeightPatch& hp, rcTempVector<int>& queue,
int region)
{
// Note: Reads to the compact heightfield are offset by border size (bs)
// since border size offset is already removed from the polymesh vertices.
queue.clear();
// Set all heights to RC_UNSET_HEIGHT.
memset(hp.data, 0xff, sizeof(unsigned short)*hp.width*hp.height);
bool empty = true;
// We cannot sample from this poly if it was created from polys
// of different regions. If it was then it could potentially be overlapping
// with polys of that region and the heights sampled here could be wrong.
if (region != RC_MULTIPLE_REGS)
{
// Copy the height from the same region, and mark region borders
// as seed points to fill the rest.
for (int hy = 0; hy < hp.height; hy++)
{
int y = hp.ymin + hy + bs;
for (int hx = 0; hx < hp.width; hx++)
{
int x = hp.xmin + hx + bs;
const rcCompactCell& c = chf.cells[x + y*chf.width];
for (int i = (int)c.index, ni = (int)(c.index + c.count); i < ni; ++i)
{
const rcCompactSpan& s = chf.spans[i];
if (s.reg == region)
{
// Store height
hp.data[hx + hy*hp.width] = s.y;
empty = false;
// If any of the neighbours is not in same region,
// add the current location as flood fill start
bool border = false;
for (int dir = 0; dir < 4; ++dir)
{
if (rcGetCon(s, dir) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(dir);
const int ay = y + rcGetDirOffsetY(dir);
const int ai = (int)chf.cells[ax + ay*chf.width].index + rcGetCon(s, dir);
const rcCompactSpan& as = chf.spans[ai];
if (as.reg != region)
{
border = true;
break;
}
}
}
if (border)
push3(queue, x, y, i);
break;
}
}
}
}
}
// if the polygon does not contain any points from the current region (rare, but happens)
// or if it could potentially be overlapping polygons of the same region,
// then use the center as the seed point.
if (empty)
seedArrayWithPolyCenter(ctx, chf, poly, npoly, verts, bs, hp, queue);
static const int RETRACT_SIZE = 256;
int head = 0;
// We assume the seed is centered in the polygon, so a BFS to collect
// height data will ensure we do not move onto overlapping polygons and
// sample wrong heights.
while (head*3 < queue.size())
{
int cx = queue[head*3+0];
int cy = queue[head*3+1];
int ci = queue[head*3+2];
head++;
if (head >= RETRACT_SIZE)
{
head = 0;
if (queue.size() > RETRACT_SIZE*3)
memmove(&queue[0], &queue[RETRACT_SIZE*3], sizeof(int)*(queue.size()-RETRACT_SIZE*3));
queue.resize(queue.size()-RETRACT_SIZE*3);
}
const rcCompactSpan& cs = chf.spans[ci];
for (int dir = 0; dir < 4; ++dir)
{
if (rcGetCon(cs, dir) == RC_NOT_CONNECTED) continue;
const int ax = cx + rcGetDirOffsetX(dir);
const int ay = cy + rcGetDirOffsetY(dir);
const int hx = ax - hp.xmin - bs;
const int hy = ay - hp.ymin - bs;
if ((unsigned int)hx >= (unsigned int)hp.width || (unsigned int)hy >= (unsigned int)hp.height)
continue;
if (hp.data[hx + hy*hp.width] != RC_UNSET_HEIGHT)
continue;
const int ai = (int)chf.cells[ax + ay*chf.width].index + rcGetCon(cs, dir);
const rcCompactSpan& as = chf.spans[ai];
hp.data[hx + hy*hp.width] = as.y;
push3(queue, ax, ay, ai);
}
}
}
...
- 生成高度数据的步骤如下:
- 如果当前
region不与多个region相连,即不为RC_MULTIPLE_REGS,则遍历当前多边形包围盒内每个cell的span,对region和多边形region相同的span进行处理。- 记录当前
cell对应的高度为span.y。 - 遍历四个方向的邻居
span,如果邻居的region和当前region不同,则将当前cell以多边形包围盒最小点为原点的坐标和span索引加入到queue中。
- 记录当前
- 如果所有
span的region都和当前region不相同,则使用seedArrayWithPolyCenter方法将多边形的中心点加入到queue中。 - 对
queue中的每个span索引,检查其四个方向的邻居,如果为可行走,且不超过多边形包围盒,同时高度没有记录过,则记录该邻居高度span.y,并将邻居位置加入到queue中。即从当前region开始扩散,直到所有span都处理完,则得到当前多边形包围盒内的所有高度信息。
- 如果当前
建立多边形细节
- 建立多边形细节方法
buildPolyDetail的实现如下:
// Recast/Source/RecastMeshDetail.cpp
static bool buildPolyDetail(rcContext* ctx, const float* in, const int nin,
const float sampleDist, const float sampleMaxError,
const int heightSearchRadius, const rcCompactHeightfield& chf,
const rcHeightPatch& hp, float* verts, int& nverts,
rcTempVector<int>& tris, rcTempVector<int>& edges, rcTempVector<int>& samples)
{
static const int MAX_VERTS = 127;
static const int MAX_TRIS = 255; // Max tris for delaunay is 2n-2-k (n=num verts, k=num hull verts).
static const int MAX_VERTS_PER_EDGE = 32;
float edge[(MAX_VERTS_PER_EDGE+1)*3];
int hull[MAX_VERTS];
int nhull = 0;
nverts = nin;
for (int i = 0; i < nin; ++i)
rcVcopy(&verts[i*3], &in[i*3]);
edges.clear();
tris.clear();
const float cs = chf.cs;
const float ics = 1.0f/cs;
// Calculate minimum extents of the polygon based on input data.
float minExtent = polyMinExtent(verts, nverts);
// Tessellate outlines.
// This is done in separate pass in order to ensure
// seamless height values across the ply boundaries.
if (sampleDist > 0)
{
for (int i = 0, j = nin-1; i < nin; j=i++)
{
const float* vj = &in[j*3];
const float* vi = &in[i*3];
bool swapped = false;
// Make sure the segments are always handled in same order
// using lexological sort or else there will be seams.
if (fabsf(vj[0]-vi[0]) < 1e-6f)
{
if (vj[2] > vi[2])
{
rcSwap(vj,vi);
swapped = true;
}
}
else
{
if (vj[0] > vi[0])
{
rcSwap(vj,vi);
swapped = true;
}
}
// Create samples along the edge.
float dx = vi[0] - vj[0];
float dy = vi[1] - vj[1];
float dz = vi[2] - vj[2];
float d = sqrtf(dx*dx + dz*dz);
int nn = 1 + (int)floorf(d/sampleDist);
if (nn >= MAX_VERTS_PER_EDGE) nn = MAX_VERTS_PER_EDGE-1;
if (nverts+nn >= MAX_VERTS)
nn = MAX_VERTS-1-nverts;
for (int k = 0; k <= nn; ++k)
{
float u = (float)k/(float)nn;
float* pos = &edge[k*3];
pos[0] = vj[0] + dx*u;
pos[1] = vj[1] + dy*u;
pos[2] = vj[2] + dz*u;
pos[1] = getHeight(pos[0],pos[1],pos[2], cs, ics, chf.ch, heightSearchRadius, hp)*chf.ch;
}
// Simplify samples.
int idx[MAX_VERTS_PER_EDGE] = {0,nn};
int nidx = 2;
for (int k = 0; k < nidx-1; )
{
const int a = idx[k];
const int b = idx[k+1];
const float* va = &edge[a*3];
const float* vb = &edge[b*3];
// Find maximum deviation along the segment.
float maxd = 0;
int maxi = -1;
for (int m = a+1; m < b; ++m)
{
float dev = distancePtSeg(&edge[m*3],va,vb);
if (dev > maxd)
{
maxd = dev;
maxi = m;
}
}
// If the max deviation is larger than accepted error,
// add new point, else continue to next segment.
if (maxi != -1 && maxd > rcSqr(sampleMaxError))
{
for (int m = nidx; m > k; --m)
idx[m] = idx[m-1];
idx[k+1] = maxi;
nidx++;
}
else
{
++k;
}
}
hull[nhull++] = j;
// Add new vertices.
if (swapped)
{
for (int k = nidx-2; k > 0; --k)
{
rcVcopy(&verts[nverts*3], &edge[idx[k]*3]);
hull[nhull++] = nverts;
nverts++;
}
}
else
{
for (int k = 1; k < nidx-1; ++k)
{
rcVcopy(&verts[nverts*3], &edge[idx[k]*3]);
hull[nhull++] = nverts;
nverts++;
}
}
}
}
// If the polygon minimum extent is small (sliver or small triangle), do not try to add internal points.
if (minExtent < sampleDist*2)
{
triangulateHull(nverts, verts, nhull, hull, nin, tris);
setTriFlags(tris, nhull, hull);
return true;
}
// Tessellate the base mesh.
// We're using the triangulateHull instead of delaunayHull as it tends to
// create a bit better triangulation for long thin triangles when there
// are no internal points.
triangulateHull(nverts, verts, nhull, hull, nin, tris);
if (tris.size() == 0)
{
// Could not triangulate the poly, make sure there is some valid data there.
ctx->log(RC_LOG_WARNING, "buildPolyDetail: Could not triangulate polygon (%d verts).", nverts);
return true;
}
if (sampleDist > 0)
{
// Create sample locations in a grid.
float bmin[3], bmax[3];
rcVcopy(bmin, in);
rcVcopy(bmax, in);
for (int i = 1; i < nin; ++i)
{
rcVmin(bmin, &in[i*3]);
rcVmax(bmax, &in[i*3]);
}
int x0 = (int)floorf(bmin[0]/sampleDist);
int x1 = (int)ceilf(bmax[0]/sampleDist);
int z0 = (int)floorf(bmin[2]/sampleDist);
int z1 = (int)ceilf(bmax[2]/sampleDist);
samples.clear();
for (int z = z0; z < z1; ++z)
{
for (int x = x0; x < x1; ++x)
{
float pt[3];
pt[0] = x*sampleDist;
pt[1] = (bmax[1]+bmin[1])*0.5f;
pt[2] = z*sampleDist;
// Make sure the samples are not too close to the edges.
if (distToPoly(nin,in,pt) > -sampleDist/2) continue;
samples.push_back(x);
samples.push_back(getHeight(pt[0], pt[1], pt[2], cs, ics, chf.ch, heightSearchRadius, hp));
samples.push_back(z);
samples.push_back(0); // Not added
}
}
// Add the samples starting from the one that has the most
// error. The procedure stops when all samples are added
// or when the max error is within treshold.
const int nsamples = static_cast<int>(samples.size()) / 4;
for (int iter = 0; iter < nsamples; ++iter)
{
if (nverts >= MAX_VERTS)
break;
// Find sample with most error.
float bestpt[3] = {0,0,0};
float bestd = 0;
int besti = -1;
for (int i = 0; i < nsamples; ++i)
{
const int* s = &samples[i*4];
if (s[3]) continue; // skip added.
float pt[3];
// The sample location is jittered to get rid of some bad triangulations
// which are cause by symmetrical data from the grid structure.
pt[0] = s[0]*sampleDist + getJitterX(i)*cs*0.1f;
pt[1] = s[1]*chf.ch;
pt[2] = s[2]*sampleDist + getJitterY(i)*cs*0.1f;
float d = distToTriMesh(pt, verts, nverts, &tris[0], static_cast<int>(tris.size()) / 4);
if (d < 0) continue; // did not hit the mesh.
if (d > bestd)
{
bestd = d;
besti = i;
rcVcopy(bestpt,pt);
}
}
// If the max error is within accepted threshold, stop tesselating.
if (bestd <= sampleMaxError || besti == -1)
break;
// Mark sample as added.
samples[besti*4+3] = 1;
// Add the new sample point.
rcVcopy(&verts[nverts*3],bestpt);
nverts++;
// Create new triangulation.
// TODO: Incremental add instead of full rebuild.
edges.clear();
tris.clear();
delaunayHull(ctx, nverts, verts, nhull, hull, tris, edges);
}
}
const int ntris = static_cast<int>(tris.size()) / 4;
if (ntris > MAX_TRIS)
{
tris.resize(MAX_TRIS*4);
ctx->log(RC_LOG_ERROR, "rcBuildPolyMeshDetail: Shrinking triangle count from %d to max %d.", ntris, MAX_TRIS);
}
setTriFlags(tris, nhull, hull);
return true;
}
...
- 建立多边形细节的步骤如下:
- 将多边形的顶点存储到
verts中。 - 通过
polyMinExtent方法,计算多边形的最小延伸范围minExtent,即多边形每个顶点到各个边最大距离,其中所有距离的最小值则为最小延伸范围。 - 如果采样距离
sampleDist大于 0 ,则遍历多边形的每条边,增加边上的顶点。- 计算边在
xz平面的长度,将边以sampleDist为步长,得到多个采样点,通过getHeight方法计算每个采样点的高度。 - 通过
distancePtSeg方法计算每个采样点(不含端点)到边的距离,取其中的最大值。- 如果距离大于
sampleMaxError,则将采样点添加到该边上作为一个顶点,把当前边分为两条新边(即进行细分)。对细分后的第一条新边上的每个采样点,重新计算到新边的距离,迭代细分。 - 如果距离不大于
sampleMaxError或者不存在采样点,则该新边已细分完成,继续处理下一条细分后的新边。
- 如果距离大于
- 将细分后得到的新顶点加入到 verts 中,细分后的所有顶点索引按顺序存储到
hull中,即新增加的顶点会存储在原始顶点之后,而hull会记录细分后多边形的顶点索引顺序。
- 计算边在
- 如果
minExtent小于sampleDist * 2,即最小延伸范围较小,不适合再内部继续细分,则- 使用
triangulateHull方法进行三角划分,得到三角面索引tris。 - 通过
setTriFlags方法标记三角形边是否为外围边。
- 使用
- 如果
minExtent不小于sampleDist * 2,即最小延伸范围足够,可以继续进行内部细分,则- 使用
triangulateHull方法进行三角划分,得到三角面索引tris。 - 如果
sampleDist大于 0 ,则需要进一步增加内部顶点。- 将
xz平面使用sampleDist为步长划分成块。 - 根据多边形的最大最小点,得到其所覆盖的块的范围。
- 遍历所有块,检查块是否要加入采样点。
- 块的
x和z坐标为块的索引乘上sampleDist,块的y坐标为多边形的最大最小高度的平均值。 - 通过
distToPoly方法,计算块坐标到多边形的最小距离,通过射线法检查坐标是否在多边形内,如果坐标在多边形内则距离取负值。 - 如果块坐标在多边形外或者最小距离不小于
sampleDist / 2,则将该块的坐标加入采样点列表samples,其中y坐标通过getHeight方法计算得到。
- 块的
- 对每一个未处理过的采样点,将
x和z坐标加上一个很小的随机偏移量,通过distToTriMesh方法,找到采样点投影到xz平面上所属的所有三角面,并计算到三角面的最小距离,作为该采样点到三角面的最终距离。 - 从所有采样点到三角面的最终距离中,找到距离最大的采样点,如果距离大于
sampleMaxError,则将该采样点加入到verts中,标记该采样点已处理,并通过delaunayHull方法对整个多边形及所有点采样点重新进行 Delaunay 三角剖分(舍弃triangulateHull和上一次delaunayHull的剖分结果)。
- 将
- 通过
setTriFlags方法标记三角形边是否为外围边。
- 使用
- 将多边形的顶点存储到
获取高度
- 计算高度方法
getHeight的实现如下:
// Recast/Source/RecastMeshDetail.cpp
...
static unsigned short getHeight(const float fx, const float fy, const float fz,
const float /*cs*/, const float ics, const float ch,
const int radius, const rcHeightPatch& hp)
{
int ix = (int)floorf(fx*ics + 0.01f);
int iz = (int)floorf(fz*ics + 0.01f);
ix = rcClamp(ix-hp.xmin, 0, hp.width - 1);
iz = rcClamp(iz-hp.ymin, 0, hp.height - 1);
unsigned short h = hp.data[ix+iz*hp.width];
if (h == RC_UNSET_HEIGHT)
{
// Special case when data might be bad.
// Walk adjacent cells in a spiral up to 'radius', and look
// for a pixel which has a valid height.
int x = 1, z = 0, dx = 1, dz = 0;
int maxSize = radius * 2 + 1;
int maxIter = maxSize * maxSize - 1;
int nextRingIterStart = 8;
int nextRingIters = 16;
float dmin = FLT_MAX;
for (int i = 0; i < maxIter; i++)
{
const int nx = ix + x;
const int nz = iz + z;
if (nx >= 0 && nz >= 0 && nx < hp.width && nz < hp.height)
{
const unsigned short nh = hp.data[nx + nz*hp.width];
if (nh != RC_UNSET_HEIGHT)
{
const float d = fabsf(nh*ch - fy);
if (d < dmin)
{
h = nh;
dmin = d;
}
}
}
// We are searching in a grid which looks approximately like this:
// __________
// |2 ______ 2|
// | |1 __ 1| |
// | | |__| | |
// | |______| |
// |__________|
// We want to find the best height as close to the center cell as possible. This means that
// if we find a height in one of the neighbor cells to the center, we don't want to
// expand further out than the 8 neighbors - we want to limit our search to the closest
// of these "rings", but the best height in the ring.
// For example, the center is just 1 cell. We checked that at the entrance to the function.
// The next "ring" contains 8 cells (marked 1 above). Those are all the neighbors to the center cell.
// The next one again contains 16 cells (marked 2). In general each ring has 8 additional cells, which
// can be thought of as adding 2 cells around the "center" of each side when we expand the ring.
// Here we detect if we are about to enter the next ring, and if we are and we have found
// a height, we abort the search.
if (i + 1 == nextRingIterStart)
{
if (h != RC_UNSET_HEIGHT)
break;
nextRingIterStart += nextRingIters;
nextRingIters += 8;
}
if ((x == z) || ((x < 0) && (x == -z)) || ((x > 0) && (x == 1 - z)))
{
int tmp = dx;
dx = -dz;
dz = tmp;
}
x += dx;
z += dz;
}
}
return h;
}
...
- 获取高度
getHeight方法的步骤为:- 根据传入的
x和z世界坐标,换算成其在上一步生成的高度数据中的单元格索引ix和iz。 - 如果高度数据中已经存在此单元格的高度值,则直接返回此高度值。
- 如果高度数据中不存在此单元格的高度值,则检查周围一圈 8 个单元格的高度值,取其中最小值返回。如果没有找到高度值,则继续检查向外一圈 16 个单元格的高度值,逐圈查找,直到找到高度值返回。返回的高度值所属的单元格和传入的坐标所属单元格越接近,则该高度值误差越小。
- 根据传入的
三角划分
- 三角划分方法
triangulateHull的实现如下:
// Recast/Source/RecastMeshDetail.cpp
...
static void triangulateHull(const int /*nverts*/, const float* verts, const int nhull, const int* hull, const int nin, rcTempVector<int>& tris)
{
int start = 0, left = 1, right = nhull-1;
// Start from an ear with shortest perimeter.
// This tends to favor well formed triangles as starting point.
float dmin = FLT_MAX;
for (int i = 0; i < nhull; i++)
{
if (hull[i] >= nin) continue; // Ears are triangles with original vertices as middle vertex while others are actually line segments on edges
int pi = prev(i, nhull);
int ni = next(i, nhull);
const float* pv = &verts[hull[pi]*3];
const float* cv = &verts[hull[i]*3];
const float* nv = &verts[hull[ni]*3];
const float d = vdist2(pv,cv) + vdist2(cv,nv) + vdist2(nv,pv);
if (d < dmin)
{
start = i;
left = ni;
right = pi;
dmin = d;
}
}
// Add first triangle
tris.push_back(hull[start]);
tris.push_back(hull[left]);
tris.push_back(hull[right]);
tris.push_back(0);
// Triangulate the polygon by moving left or right,
// depending on which triangle has shorter perimeter.
// This heuristic was chose empirically, since it seems
// handle tessellated straight edges well.
while (next(left, nhull) != right)
{
// Check to see if se should advance left or right.
int nleft = next(left, nhull);
int nright = prev(right, nhull);
const float* cvleft = &verts[hull[left]*3];
const float* nvleft = &verts[hull[nleft]*3];
const float* cvright = &verts[hull[right]*3];
const float* nvright = &verts[hull[nright]*3];
const float dleft = vdist2(cvleft, nvleft) + vdist2(nvleft, cvright);
const float dright = vdist2(cvright, nvright) + vdist2(cvleft, nvright);
if (dleft < dright)
{
tris.push_back(hull[left]);
tris.push_back(hull[nleft]);
tris.push_back(hull[right]);
tris.push_back(0);
left = nleft;
}
else
{
tris.push_back(hull[left]);
tris.push_back(hull[nright]);
tris.push_back(hull[right]);
tris.push_back(0);
right = nright;
}
}
}
...
- 三角划分
triangulateHull方法的步骤为:- 遍历多边形所有原本的顶点,计算原顶点和左右相邻的两个细化后顶点组成的三角形的周长,找到周长最小的原顶点,作为三角划分的起始点,将原顶点、左侧相邻顶点和右侧相邻顶点作为第一个三角形的三个顶点,将索引加入到
tris中。 - 计算左侧三角形周长(左侧顶点、左侧顶点的下一个顶点、右侧顶点)和右侧三角形周长(右侧顶点、右侧顶点的上一个顶点、左侧顶点),比较周长大小。
- 如果左侧三角形周长小,则将左侧顶点、左侧顶点的下一个顶点、右侧顶点作为下一个三角形的三个顶点,将索引加入到
tris中,并将左侧顶点的下一个顶点作为新的左侧顶点。 - 如果右侧三角形周长小或者两者周长相等,则将右侧顶点、右侧顶点的上一个顶点、左侧顶点作为下一个三角形的三个顶点,将索引加入到
tris中,并将右侧顶点的上一个顶点作为新的右侧顶点。 - 重复上述步骤,直到左侧顶点的下一个顶点为右侧顶点,则划分完成。
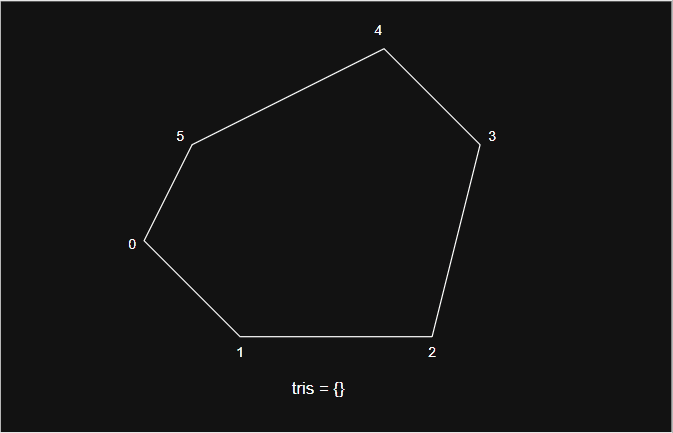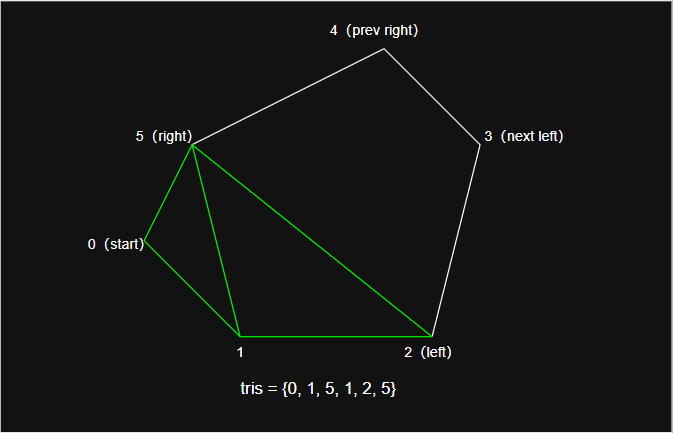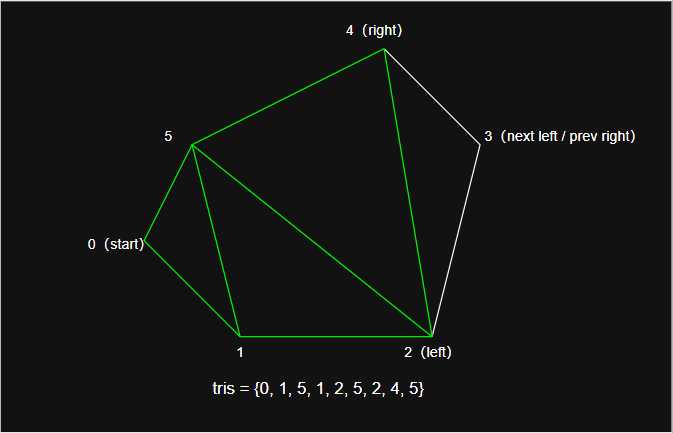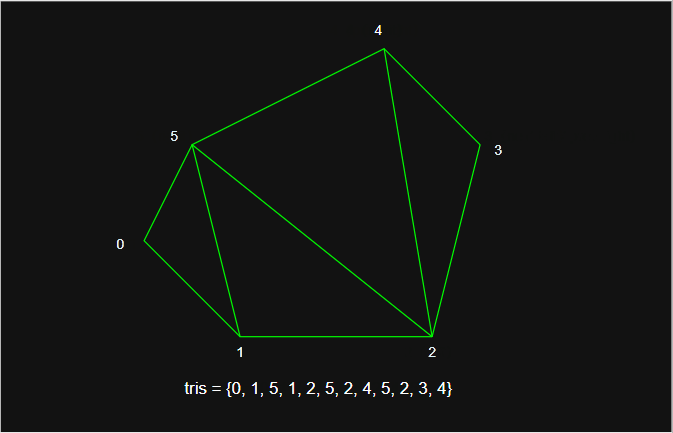
- 如果左侧三角形周长小,则将左侧顶点、左侧顶点的下一个顶点、右侧顶点作为下一个三角形的三个顶点,将索引加入到
- 遍历多边形所有原本的顶点,计算原顶点和左右相邻的两个细化后顶点组成的三角形的周长,找到周长最小的原顶点,作为三角划分的起始点,将原顶点、左侧相邻顶点和右侧相邻顶点作为第一个三角形的三个顶点,将索引加入到
计算点到三角面距离
- 计算点到三角面距离方法
distPtTri的实现如下:
// Recast/Source/RecastMeshDetail.cpp
...
static float distPtTri(const float* p, const float* a, const float* b, const float* c)
{
float v0[3], v1[3], v2[3];
rcVsub(v0, c,a);
rcVsub(v1, b,a);
rcVsub(v2, p,a);
const float dot00 = vdot2(v0, v0);
const float dot01 = vdot2(v0, v1);
const float dot02 = vdot2(v0, v2);
const float dot11 = vdot2(v1, v1);
const float dot12 = vdot2(v1, v2);
// Compute barycentric coordinates
const float invDenom = 1.0f / (dot00 * dot11 - dot01 * dot01);
const float u = (dot11 * dot02 - dot01 * dot12) * invDenom;
float v = (dot00 * dot12 - dot01 * dot02) * invDenom;
// If point lies inside the triangle, return interpolated y-coord.
static const float EPS = 1e-4f;
if (u >= -EPS && v >= -EPS && (u+v) <= 1+EPS)
{
const float y = a[1] + v0[1]*u + v1[1]*v;
return fabsf(y-p[1]);
}
return FLT_MAX;
}
...
- 计算点 P 到三角面 ABC 距离,是通过先检查点 P 是否在三角形
xz平面内,再进行插值计算得到。 - 点 P 在
xz平面可以表示为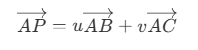
- 两边分别乘上向量 AB 和 AC ,可以得到
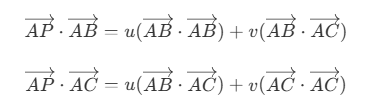 解方程组可以得到
解方程组可以得到
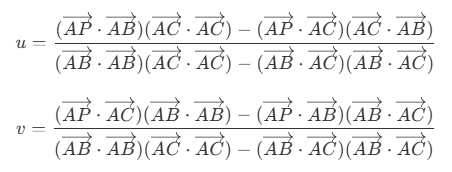
- 如果点 P 在三角形内,则点 P 为三角形的重心坐标,则
u和v都大于 0,且u + v不超过 1。此时点 P 的高度则可以通过插值得到,即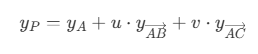
Delaunay 三角剖分
- Delaunay 三角剖分方法
delaunayHull的实现如下:
// Recast/Source/RecastMeshDetail.cpp
...
static void delaunayHull(rcContext* ctx, const int npts, const float* pts,
const int nhull, const int* hull,
rcTempVector<int>& tris, rcTempVector<int>& edges)
{
int nfaces = 0;
int nedges = 0;
const int maxEdges = npts*10;
edges.resize(maxEdges*4);
for (int i = 0, j = nhull-1; i < nhull; j=i++)
addEdge(ctx, &edges[0], nedges, maxEdges, hull[j],hull[i], EV_HULL, EV_UNDEF);
int currentEdge = 0;
while (currentEdge < nedges)
{
if (edges[currentEdge*4+2] == EV_UNDEF)
completeFacet(ctx, pts, npts, &edges[0], nedges, maxEdges, nfaces, currentEdge);
if (edges[currentEdge*4+3] == EV_UNDEF)
completeFacet(ctx, pts, npts, &edges[0], nedges, maxEdges, nfaces, currentEdge);
currentEdge++;
}
// Create tris
tris.resize(nfaces*4);
for (int i = 0; i < nfaces*4; ++i)
tris[i] = -1;
for (int i = 0; i < nedges; ++i)
{
const int* e = &edges[i*4];
if (e[3] >= 0)
{
// Left face
int* t = &tris[e[3]*4];
if (t[0] == -1)
{
t[0] = e[0];
t[1] = e[1];
}
else if (t[0] == e[1])
t[2] = e[0];
else if (t[1] == e[0])
t[2] = e[1];
}
if (e[2] >= 0)
{
// Right
int* t = &tris[e[2]*4];
if (t[0] == -1)
{
t[0] = e[1];
t[1] = e[0];
}
else if (t[0] == e[0])
t[2] = e[1];
else if (t[1] == e[1])
t[2] = e[0];
}
}
for (int i = 0; i < tris.size()/4; ++i)
{
int* t = &tris[i*4];
if (t[0] == -1 || t[1] == -1 || t[2] == -1)
{
ctx->log(RC_LOG_WARNING, "delaunayHull: Removing dangling face %d [%d,%d,%d].", i, t[0],t[1],t[2]);
t[0] = tris[tris.size()-4];
t[1] = tris[tris.size()-3];
t[2] = tris[tris.size()-2];
t[3] = tris[tris.size()-1];
tris.resize(tris.size()-4);
--i;
}
}
}
...
delaunayHull方法进行三角剖分的步骤为:- 遍历细化后的多边形的每条边,加入到
edge中,并标记边的逆时针方向为EV_HULL,即逆时针方向归属于外轮廓的某个三角形索引,顺时针方向为EV_UNDEF,顺时针方向暂无归属。- 三角形的每条边最多能与另一个三角形共用,此时逆时针方向的边归属于一个三角形,顺时针方向的边归属于另一个三角形。
- 通过
completeFacet方法,对edge中的每一条边进行处理。- 遍历所有在当前边左侧的顶点,如果当前没有外接圆,则计算当前边和当前顶点组成的三角形的外接圆,如果当前有外接圆,则计算当前顶点到当前外接圆圆心的距离。
- 如果距离大于外接圆半径,则跳过当前顶点。
- 如果距离小于外接圆半径,则记录当前顶点,并使用当前顶点重新计算新的外接圆。
- 如果距离等于外接圆半径,则检查当前顶点和当前顶点组成的三角形的另外两条边,和
edge中的边是否相交。如果都不相交,则记录当前顶点,并使用当前顶点重新计算新的外接圆。 - 如果有找到符合条件的顶点(即存在外接圆且圆心最靠右,在边的左侧弧长最小),则将该三角形不在
edge中的新边加入到edge中,并设置三条边方向归属的三角形索引。 - 继续取下一条边,重复进行处理,直到
edge中所有边都处理完成。
- 遍历
edge中的每一条边,根据边方向归属的三角形索引,将顶点索引加入到tris中。(源码中使用e[3]处理逆时针方向的边,e[2]处理顺时针方向的边,和addEdge、completeFacet方法中处理的顺序相反,可能有误?)
- 遍历细化后的多边形的每条边,加入到
- 剖分的示意图如下,其中红色线代表当前处理的边,黄色线代表边标记了逆时针方向,绿色边代表边标记了逆时针和顺时针方向。

计算三角形外接圆
- 计算三角形外接圆圆心和半径方法
circumCircle的实现如下:
// Recast/Source/RecastMeshDetail.cpp
...
static bool circumCircle(const float* p1, const float* p2, const float* p3,
float* c, float& r)
{
static const float EPS = 1e-6f;
// Calculate the circle relative to p1, to avoid some precision issues.
const float v1[3] = {0,0,0};
float v2[3], v3[3];
rcVsub(v2, p2,p1);
rcVsub(v3, p3,p1);
const float cp = vcross2(v1, v2, v3);
if (fabsf(cp) > EPS)
{
const float v1Sq = vdot2(v1,v1);
const float v2Sq = vdot2(v2,v2);
const float v3Sq = vdot2(v3,v3);
c[0] = (v1Sq*(v2[2]-v3[2]) + v2Sq*(v3[2]-v1[2]) + v3Sq*(v1[2]-v2[2])) / (2*cp);
c[1] = 0;
c[2] = (v1Sq*(v3[0]-v2[0]) + v2Sq*(v1[0]-v3[0]) + v3Sq*(v2[0]-v1[0])) / (2*cp);
r = vdist2(c, v1);
rcVadd(c, c, p1);
return true;
}
rcVcopy(c, p1);
r = 0;
return false;
}
...
- 三角形的外接圆,圆心
c到三个顶点p1、p2、p3的距离相等,则有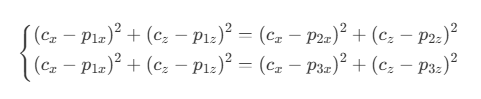 整理可得
整理可得
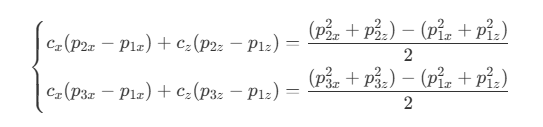 求解方程有
求解方程有
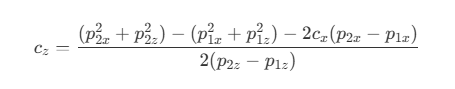 代入可得
代入可得
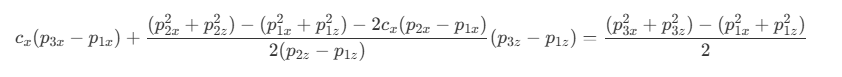 整理可得
整理可得
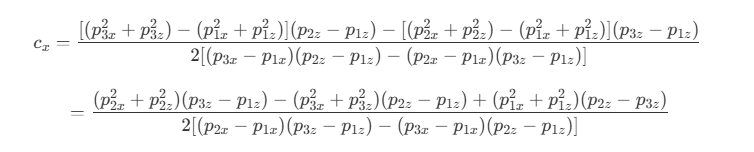 其中
其中
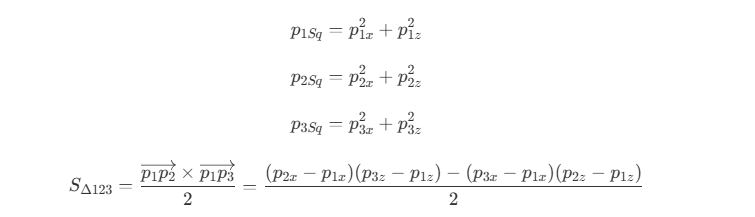 则有
则有
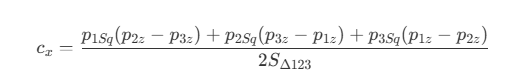 同理可得
同理可得
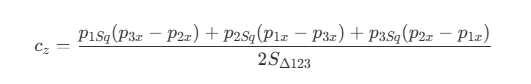
circumCircle方法先将三角形的三个顶点都偏移了p1的位置,再通过vcross2方法检查三点是否共线,非共线再进行计算,最终得到的圆心坐标再加上p1即为三角形的外接圆圆心c。
空圆特性
- 三角剖分算法的基础概念如下(引自百度百科):
- 三角剖分
假设
V是二维实数域上的有限点集,边e是由点集中的点作为端点构成的封闭线段,E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G,该平面图满足条件: - 除了端点,平面图中的边不包含点集中的任何点。 - 没有相交边。 - 平面图中所有的面都是三角面,且所有三角面的合集是散点集V的凸包。 - Delaunay 边
- 假设
E中的一条边e(两个端点为a、b),e若满足下列条件,则称之为 Delaunay 边:- 存在一个圆经过
a、b两点,圆内(注意是圆内,圆上最多三点共圆)不含点集V中任何其他的点(空圆特性)。
- 存在一个圆经过
- 假设
- Delaunay三角剖分
- 如果点集
V的一个三角剖分T只包含 Delaunay 边,那么该三角剖分称为 Delaunay 三角剖分。
- 如果点集
- 三角剖分
假设
- 从概念上可以看出,Delaunay 三角剖分的每一个三角形需要满足两个条件:
- 空圆特性,即每个三角形内不存在有其他顶点。
- 三角形的边不能和其他边相交。
delaunayHull对所有边计算外接圆时仅检查左侧的所有顶点,得到外接圆后,其在边的左侧部分中不存在其他顶点。而为了满足空圆特性,需要确保外接圆在边的右侧部分中也不存在其他顶点。- 由于算法处理是从多边形的边开始的,在之前的建立多边形网格步骤中,轮廓进行了三角划分及合并得到多个多边形,最终得到的每个多边形都是凸多边形,而凸多边形的每条边的右侧,都不存在其他顶点,所以最外层外接圆在边的右侧部分中不存在其他顶点。
- 如图中的红色边
3-0,其右侧为多边形外部,不存在其他顶点。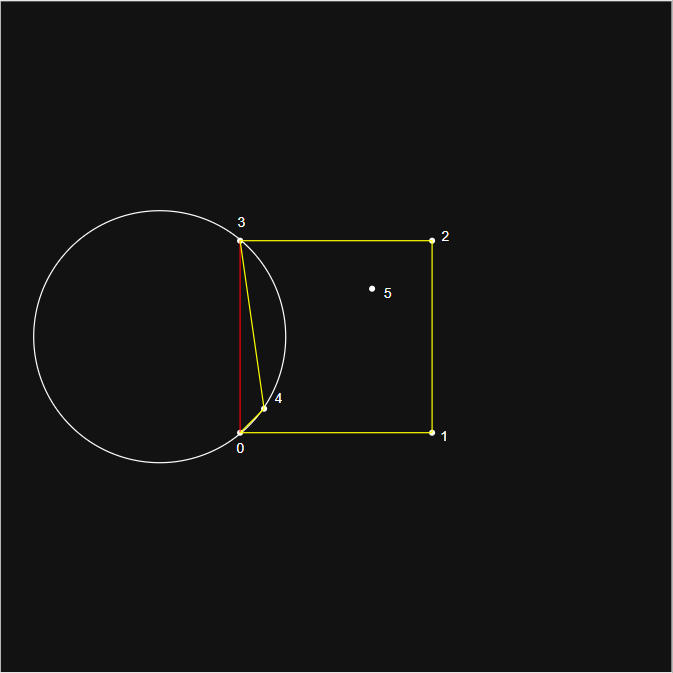
- 如图中的红色边
- 由于所有新增的内部边都是通过外层的外接圆得到的,都处在外层的外接圆上。当内部边找到外接圆后,两个圆相交且交点线即为当前内部边。此时,边的左侧部分中不存在其他顶点,而边的右侧部分,必定为外层外接圆的真子集,即边的右侧部分同样不存在其他顶点,因此内部边的外接圆满足空圆特性。
- 如图中的红色边
3-4,处在外层的外接圆A-A'上,以及内部外接圆B-B'上,其中3-B'-4为A-A'的真子集,因此3-B'-4中不存在其他顶点,即B-B'满足空圆特性。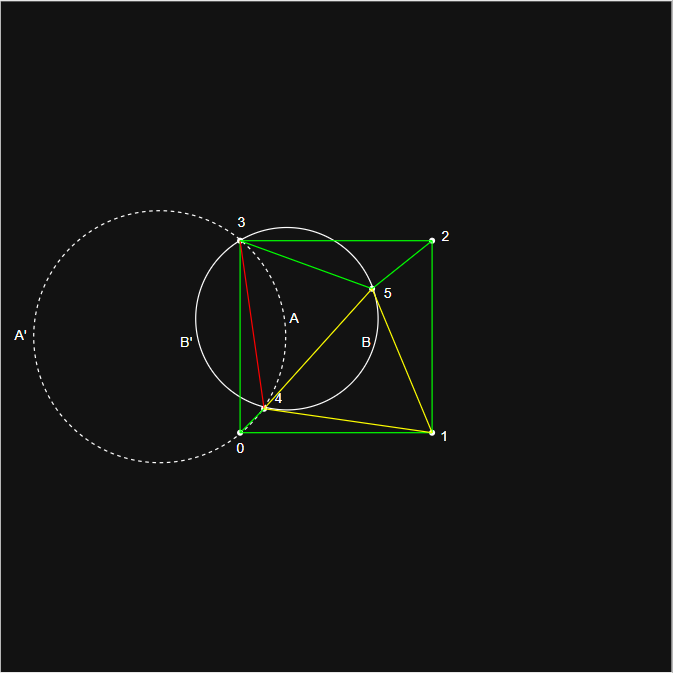
- 如图中的红色边
- 由于算法处理是从多边形的边开始的,在之前的建立多边形网格步骤中,轮廓进行了三角划分及合并得到多个多边形,最终得到的每个多边形都是凸多边形,而凸多边形的每条边的右侧,都不存在其他顶点,所以最外层外接圆在边的右侧部分中不存在其他顶点。
八、生成导航数据
- 生成导航数据的主要步骤为:
- 通过
dtCreateNavMeshData方法创建导航网格数据,数据包括:- 头部信息。
- 顶点坐标。
- 多边形信息
dtPoly。 - 链接信息(仅预留空间,在加载时创建)。
- 细节多边形(网格
dtPolyDetail、顶点坐标、三角面索引)。 - BVH 树
dtBVNode。 - 离网连接信息
dtOffMeshConnection。
- 初始化导航网格。
- 初始化导航网格查询。
- 通过
创建导航网格数据
头部信息
- 头部信息的结构为
dtMeshHeader,其内容如下:
// Detour/Include/DetourNavMesh.h
...
struct dtMeshHeader
{
int magic; /// 用于检测导航图块数据兼容性的标识值(DT_NAVMESH_MAGIC)
int version; /// 用于检测导航图块数据兼容性的版本号(这里使用 DT_NAVMESH_VERSION)
int x; /// 瓦片网格中的 x 坐标(未设置)
int y; /// 瓦片网格中的 y 坐标(未设置)
int layer; /// 瓦片网格中的层 id(未设置)
unsigned int userId; /// 用户定义的 id(未设置)
int polyCount; /// 多边形数量(细化前的多边形数量 + 离网连接数量)
int vertCount; /// 顶点数量(细化前的顶点数量 + 离网连接数量的 2 倍)
int maxLinkCount; /// 已分配的链接数量(多边形的边数量 + 边界边数量 * 2 + 离网连接的链接数量 * 2)
int detailMeshCount; /// 细节网格中的子网格数量(细节多边形的数量)
/// 细节网格中的顶点数量(内部细化增加的顶点数量)
int detailVertCount;
int detailTriCount; /// 细节网格的三角面数量(没有细节网格则为多边形的三角面数量)
int bvNodeCount; /// BVH 树节点数量(细节多边形数量 * 2)
int offMeshConCount; /// 离网连接数量
int offMeshBase; /// 首个离网连接在导航网格数据顶点中的存储索引
float walkableHeight; /// 可行走高度(真实距离,非格子)
float walkableRadius; /// 可行走半径(真实距离,非格子)
float walkableClimb; /// 可跨越高度(真实距离,非格子)
float bmin[3]; /// 细节网格的 AABB 包围盒的最小值坐标(真实距离,非格子)
float bmax[3]; /// 细节网格的 AABB 包围盒的最大值坐标(真实距离,非格子)
/// 边界体积量化因子(1 / 单元格尺寸)
float bvQuantFactor;
};
...
- 在初始化的
rcConfig配置中,walkableHeight、walkableRadius、walkableClimb都转换成了格子距离,而在最终生成的导航网格数据中,则转换成了真实距离。
顶点坐标
- 顶点坐标的设置如下:
// Detour/Source/DetourNavMeshBuilder.cpp
...
bool dtCreateNavMeshData(dtNavMeshCreateParams* params, unsigned char** outData, int* outDataSize)
{
...
const int offMeshVertsBase = params->vertCount;
const int offMeshPolyBase = params->polyCount;
// Store vertices
// Mesh vertices
for (int i = 0; i < params->vertCount; ++i)
{
const unsigned short* iv = ¶ms->verts[i*3];
float* v = &navVerts[i*3];
v[0] = params->bmin[0] + iv[0] * params->cs;
v[1] = params->bmin[1] + iv[1] * params->ch;
v[2] = params->bmin[2] + iv[2] * params->cs;
}
// Off-mesh link vertices.
int n = 0;
for (int i = 0; i < params->offMeshConCount; ++i)
{
// Only store connections which start from this tile.
if (offMeshConClass[i*2+0] == 0xff)
{
const float* linkv = ¶ms->offMeshConVerts[i*2*3];
float* v = &navVerts[(offMeshVertsBase + n*2)*3];
dtVcopy(&v[0], &linkv[0]);
dtVcopy(&v[3], &linkv[3]);
n++;
}
}
...
}
...
- 顶点坐标包括直接连接和离网连接两种,对于直接连接,则将细化前的顶点坐标转换为真实世界坐标系下的坐标,存入到
navVerts中,对于离网连接,则将离网连接的起始坐标和结束坐标存入到navVerts中。
多边形信息
- 多边形信息使用 ``dtPoly` 结构存储,其内容如下:
// Detour/Include/DetourNavMesh.h
...
struct dtPoly
{
/// 多边形的第一个链接索引
unsigned int firstLink;
/// 多边形的顶点索引
unsigned short verts[DT_VERTS_PER_POLYGON];
/// 多边形顶点的邻居多边形索引 + 1
unsigned short neis[DT_VERTS_PER_POLYGON];
/// 多边形用户自定义标记 rcPolyMesh.flags
unsigned short flags;
/// 每个多边形的顶点数量
unsigned char vertCount;
/// 多边形区域和类型标记,低 6 位为区域,高 2 位为类型
unsigned char areaAndtype;
/// 设置区域方法
inline void setArea(unsigned char a) { areaAndtype = (areaAndtype & 0xc0) | (a & 0x3f); }
/// 设置类型方法
inline void setType(unsigned char t) { areaAndtype = (areaAndtype & 0x3f) | (t << 6); }
/// 获取区域方法
inline unsigned char getArea() const { return areaAndtype & 0x3f; }
/// 获取类型方法
inline unsigned char getType() const { return areaAndtype >> 6; }
};
...
- 多边形信息的设置如下:
// Detour/Source/DetourNavMeshBuilder.cpp
...
bool dtCreateNavMeshData(dtNavMeshCreateParams* params, unsigned char** outData, int* outDataSize)
{
...
const unsigned short* src = params->polys;
for (int i = 0; i < params->polyCount; ++i)
{
dtPoly* p = &navPolys[i];
p->vertCount = 0;
p->flags = params->polyFlags[i];
p->setArea(params->polyAreas[i]);
p->setType(DT_POLYTYPE_GROUND);
for (int j = 0; j < nvp; ++j)
{
if (src[j] == MESH_NULL_IDX) break;
p->verts[j] = src[j];
if (src[nvp+j] & 0x8000)
{
// Border or portal edge.
unsigned short dir = src[nvp+j] & 0xf;
if (dir == 0xf) // Border
p->neis[j] = 0;
else if (dir == 0) // Portal x-
p->neis[j] = DT_EXT_LINK | 4;
else if (dir == 1) // Portal z+
p->neis[j] = DT_EXT_LINK | 2;
else if (dir == 2) // Portal x+
p->neis[j] = DT_EXT_LINK | 0;
else if (dir == 3) // Portal z-
p->neis[j] = DT_EXT_LINK | 6;
}
else
{
// Normal connection
p->neis[j] = src[nvp+j]+1;
}
p->vertCount++;
}
src += nvp*2;
}
// Off-mesh connection vertices.
n = 0;
for (int i = 0; i < params->offMeshConCount; ++i)
{
// Only store connections which start from this tile.
if (offMeshConClass[i*2+0] == 0xff)
{
dtPoly* p = &navPolys[offMeshPolyBase+n];
p->vertCount = 2;
p->verts[0] = (unsigned short)(offMeshVertsBase + n*2+0);
p->verts[1] = (unsigned short)(offMeshVertsBase + n*2+1);
p->flags = params->offMeshConFlags[i];
p->setArea(params->offMeshConAreas[i]);
p->setType(DT_POLYTYPE_OFFMESH_CONNECTION);
n++;
}
}
...
}
...
- 多边形信息的设置主要为
dtPoly结构的设置,根据记录在polys[i * nvp * 2 + nvp + j]中(i为多边形索引,j为顶点索引)的邻居信息进行设置,其中顶点的邻居neis设置分为入口边界和内部两种情况。- 对于入口边界邻居,在建立多边形网格步骤的
rcBuildPolyMesh方法中,对于borderSize大于 0 的多边形,polys对应的邻居信息为边界标记信息,左入口边界为0x8000,上入口边界为0x8001,右入口边界为0x8002,下入口边界为0x8003,根据polys中的值重新设置neis的值。 - 对于内部邻居,则
neis为polys对应的邻居信息(多边形索引)+ 1。其中+ 1是用于将0作为无邻居的处理,和多边形索引0区分开。
- 对于入口边界邻居,在建立多边形网格步骤的
firstLink的设置这里未进行,会在后续初始化过程中进行设置。
链接信息
- 链接信息使用
dtLink结构存储,其内容如下:
// Detour/Include/DetourNavMesh.h
...
struct dtLink
{
dtPolyRef ref; /// 邻居多边形索引
unsigned int next; /// 下一个链接索引
unsigned char edge; /// 当前链接对应的多边形边的索引
unsigned char side; /// 如果为包围盒链接,则表示对应的方向(左、上、右、下)
unsigned char bmin; /// 如果为包围盒链接,则表示最小的子边区域。
unsigned char bmax; /// 如果为包围盒链接,则表示最大的子边区域。
};
...
- 此处并未进行链接信息的设置,仅预留了空间,后续在初始化过程进行设置。
细节多边形
- 如果存在细节多边形,则需要对网格参数、顶点坐标、三角面索引进行设置,其代码如下:
// Detour/Source/DetourNavMeshBuilder.cpp
...
bool dtCreateNavMeshData(dtNavMeshCreateParams* params, unsigned char** outData, int* outDataSize)
{
...
if (params->detailMeshes)
{
unsigned short vbase = 0;
for (int i = 0; i < params->polyCount; ++i)
{
dtPolyDetail& dtl = navDMeshes[i];
const int vb = (int)params->detailMeshes[i*4+0];
const int ndv = (int)params->detailMeshes[i*4+1];
const int nv = navPolys[i].vertCount;
dtl.vertBase = (unsigned int)vbase;
dtl.vertCount = (unsigned char)(ndv-nv);
dtl.triBase = (unsigned int)params->detailMeshes[i*4+2];
dtl.triCount = (unsigned char)params->detailMeshes[i*4+3];
// Copy vertices except the first 'nv' verts which are equal to nav poly verts.
if (ndv-nv)
{
memcpy(&navDVerts[vbase*3], ¶ms->detailVerts[(vb+nv)*3], sizeof(float)*3*(ndv-nv));
vbase += (unsigned short)(ndv-nv);
}
}
// Store triangles.
memcpy(navDTris, params->detailTris, sizeof(unsigned char)*4*params->detailTriCount);
}
else
{
// Create dummy detail mesh by triangulating polys.
int tbase = 0;
for (int i = 0; i < params->polyCount; ++i)
{
dtPolyDetail& dtl = navDMeshes[i];
const int nv = navPolys[i].vertCount;
dtl.vertBase = 0;
dtl.vertCount = 0;
dtl.triBase = (unsigned int)tbase;
dtl.triCount = (unsigned char)(nv-2);
// Triangulate polygon (local indices).
for (int j = 2; j < nv; ++j)
{
unsigned char* t = &navDTris[tbase*4];
t[0] = 0;
t[1] = (unsigned char)(j-1);
t[2] = (unsigned char)j;
// Bit for each edge that belongs to poly boundary.
t[3] = (1<<2);
if (j == 2) t[3] |= (1<<0);
if (j == nv-1) t[3] |= (1<<4);
tbase++;
}
}
}
...
}
...
- 细节多边形存储的顶点信息,都是相对于原始多边形的,即相对于
navPolys数组中的多边形中增加的顶点,三角面则为三角剖分后的三角面,网格信息使用dtPolyDetail结构存储,其内容如下:
// Detour/Include/DetourNavMesh.h
...
struct dtPolyDetail
{
unsigned int vertBase; /// 细化后增加的首个顶点,在所有细化顶点中的索引
unsigned int triBase; /// 细化后的首个三角面,在所有三角面中的索引
unsigned char vertCount; /// 细化后增加的顶点数量
unsigned char triCount; /// 细化后的三角面数量
};
...
- 对于没有细节多边形的情况,则自行划分三角面,以第一个顶点和除该顶点外的每一条边划分三角面,并设置三角面的外围边标记(
tris[3])。
BVH 树
- BVH 树通过
createBVTree方法进行构建,其代码如下:
// Detour/Source/DetourNavMeshBuilder.cpp
...
static int createBVTree(dtNavMeshCreateParams* params, dtBVNode* nodes, int /*nnodes*/)
{
// Build tree
float quantFactor = 1 / params->cs;
BVItem* items = (BVItem*)dtAlloc(sizeof(BVItem)*params->polyCount, DT_ALLOC_TEMP);
for (int i = 0; i < params->polyCount; i++)
{
BVItem& it = items[i];
it.i = i;
// Calc polygon bounds. Use detail meshes if available.
if (params->detailMeshes)
{
int vb = (int)params->detailMeshes[i*4+0];
int ndv = (int)params->detailMeshes[i*4+1];
float bmin[3];
float bmax[3];
const float* dv = ¶ms->detailVerts[vb*3];
dtVcopy(bmin, dv);
dtVcopy(bmax, dv);
for (int j = 1; j < ndv; j++)
{
dtVmin(bmin, &dv[j * 3]);
dtVmax(bmax, &dv[j * 3]);
}
// BV-tree uses cs for all dimensions
it.bmin[0] = (unsigned short)dtClamp((int)((bmin[0] - params->bmin[0])*quantFactor), 0, 0xffff);
it.bmin[1] = (unsigned short)dtClamp((int)((bmin[1] - params->bmin[1])*quantFactor), 0, 0xffff);
it.bmin[2] = (unsigned short)dtClamp((int)((bmin[2] - params->bmin[2])*quantFactor), 0, 0xffff);
it.bmax[0] = (unsigned short)dtClamp((int)((bmax[0] - params->bmin[0])*quantFactor), 0, 0xffff);
it.bmax[1] = (unsigned short)dtClamp((int)((bmax[1] - params->bmin[1])*quantFactor), 0, 0xffff);
it.bmax[2] = (unsigned short)dtClamp((int)((bmax[2] - params->bmin[2])*quantFactor), 0, 0xffff);
}
else
{
const unsigned short* p = ¶ms->polys[i*params->nvp * 2];
it.bmin[0] = it.bmax[0] = params->verts[p[0] * 3 + 0];
it.bmin[1] = it.bmax[1] = params->verts[p[0] * 3 + 1];
it.bmin[2] = it.bmax[2] = params->verts[p[0] * 3 + 2];
for (int j = 1; j < params->nvp; ++j)
{
if (p[j] == MESH_NULL_IDX) break;
unsigned short x = params->verts[p[j] * 3 + 0];
unsigned short y = params->verts[p[j] * 3 + 1];
unsigned short z = params->verts[p[j] * 3 + 2];
if (x < it.bmin[0]) it.bmin[0] = x;
if (y < it.bmin[1]) it.bmin[1] = y;
if (z < it.bmin[2]) it.bmin[2] = z;
if (x > it.bmax[0]) it.bmax[0] = x;
if (y > it.bmax[1]) it.bmax[1] = y;
if (z > it.bmax[2]) it.bmax[2] = z;
}
// Remap y
it.bmin[1] = (unsigned short)dtMathFloorf((float)it.bmin[1] * params->ch / params->cs);
it.bmax[1] = (unsigned short)dtMathCeilf((float)it.bmax[1] * params->ch / params->cs);
}
}
int curNode = 0;
subdivide(items, params->polyCount, 0, params->polyCount, curNode, nodes);
dtFree(items);
return curNode;
}
...
- 构建 BVH 树时,会将每个多边形的包围盒信息存储在
BVItem结构中,作为树的节点,通过subdivide方法,每次选择所有子节点的整体包围盒最长的轴,将子节点进行划分,最终得到 BVH 树。
离网连接信息
- 离网连接信息使用
dtOffMeshConnection结构存储,其内容为:
// Detour/Include/DetourNavMesh.h
...
struct dtOffMeshConnection
{
/// 连接的起始点和终点坐标
float pos[6];
/// 连接点的半径
float rad;
/// 连接多边形引用
unsigned short poly;
/// 内部链接标记
unsigned char flags;
/// 结束点边
unsigned char side;
/// 用户定义的 id
unsigned int userId;
};
...
初始化导航网格
- 初始化导航网格过程,即创建
dtNavMesh对象,通过其init方法,对数据完成初始化后,通过addTile方法创建dtMeshTile对象,其结构如下:
// Detour/Include/DetourNavMesh.h
...
struct dtMeshTile
{
unsigned int salt; /// 修改计数器,初始化为 1
unsigned int linksFreeList; ///< Index to the next free link.
dtMeshHeader* header; ///< The tile header.
dtPoly* polys; /// 导航网格数据的多边形信息
float* verts; /// 导航网格数据的顶点坐标
dtLink* links; /// 导航网格数据的链接信息,初始化时无数据
dtPolyDetail* detailMeshes; /// 导航网格数据的细节多边形网格
/// 导航网格数据的细节多边形顶点坐标
float* detailVerts;
/// 导航网格数据的细节多边形三角面索引
unsigned char* detailTris;
/// 导航网格数据的 BVH 树
dtBVNode* bvTree;
dtOffMeshConnection* offMeshCons; /// 导航网格数据的离网连接信息
unsigned char* data; /// 导航网格数据的原始数据
int dataSize; /// 导航网格数据的原始数据大小
int flags; /// 标记信息,初始化为 dtTileFlags.DT_TILE_FREE_DATA
dtMeshTile* next; /// 下一个空闲 tile,初始化为 0
...
};
...
- 数据初始化
init方法的代码如下:
// Detour/Source/DetourNavMesh.cpp
...
dtStatus dtNavMesh::init(const dtNavMeshParams* params)
{
memcpy(&m_params, params, sizeof(dtNavMeshParams));
dtVcopy(m_orig, params->orig);
m_tileWidth = params->tileWidth;
m_tileHeight = params->tileHeight;
// Init tiles
m_maxTiles = params->maxTiles;
m_tileLutSize = dtNextPow2(params->maxTiles/4);
if (!m_tileLutSize) m_tileLutSize = 1;
m_tileLutMask = m_tileLutSize-1;
m_tiles = (dtMeshTile*)dtAlloc(sizeof(dtMeshTile)*m_maxTiles, DT_ALLOC_PERM);
if (!m_tiles)
return DT_FAILURE | DT_OUT_OF_MEMORY;
m_posLookup = (dtMeshTile**)dtAlloc(sizeof(dtMeshTile*)*m_tileLutSize, DT_ALLOC_PERM);
if (!m_posLookup)
return DT_FAILURE | DT_OUT_OF_MEMORY;
memset(m_tiles, 0, sizeof(dtMeshTile)*m_maxTiles);
memset(m_posLookup, 0, sizeof(dtMeshTile*)*m_tileLutSize);
m_nextFree = 0;
for (int i = m_maxTiles-1; i >= 0; --i)
{
m_tiles[i].salt = 1;
m_tiles[i].next = m_nextFree;
m_nextFree = &m_tiles[i];
}
// Init ID generator values.
#ifndef DT_POLYREF64
m_tileBits = dtIlog2(dtNextPow2((unsigned int)params->maxTiles));
m_polyBits = dtIlog2(dtNextPow2((unsigned int)params->maxPolys));
// Ensure that the bits of poly ref do not overflow.
dtAssert(m_tileBits + m_polyBits <= 31);
// Only allow 31 salt bits, since the salt mask is calculated using 32bit uint and it will overflow.
m_saltBits = dtMin((unsigned int)31, 32 - m_tileBits - m_polyBits);
if (m_saltBits < 10)
return DT_FAILURE | DT_INVALID_PARAM;
#endif
return DT_SUCCESS;
}
...
- 其中,单瓦片网格在初始化的时候只会调用一次
addTile方法创建一个dtMeshTile对象,存入到m_nextFree中,所以params->maxTiles为1,则m_tileLutSize为1,m_tileLutMask为0。各结构的概念如图: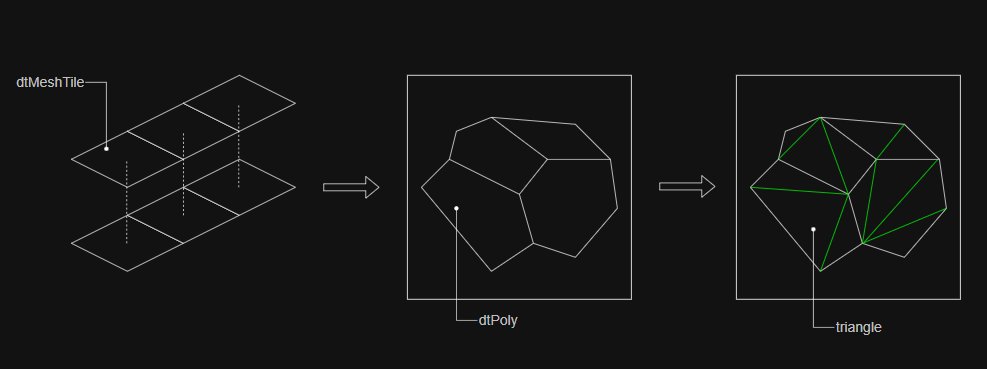
addTile方法的实现如下:
// Detour/Source/DetourNavMesh.cpp
...
dtStatus dtNavMesh::addTile(unsigned char* data, int dataSize, int flags,
dtTileRef lastRef, dtTileRef* result)
{
// Make sure the data is in right format.
dtMeshHeader* header = (dtMeshHeader*)data;
if (header->magic != DT_NAVMESH_MAGIC)
return DT_FAILURE | DT_WRONG_MAGIC;
if (header->version != DT_NAVMESH_VERSION)
return DT_FAILURE | DT_WRONG_VERSION;
#ifndef DT_POLYREF64
// Do not allow adding more polygons than specified in the NavMesh's maxPolys constraint.
// Otherwise, the poly ID cannot be represented with the given number of bits.
if (m_polyBits < dtIlog2(dtNextPow2((unsigned int)header->polyCount)))
return DT_FAILURE | DT_INVALID_PARAM;
#endif
// Make sure the location is free.
if (getTileAt(header->x, header->y, header->layer))
return DT_FAILURE | DT_ALREADY_OCCUPIED;
// Allocate a tile.
dtMeshTile* tile = 0;
if (!lastRef)
{
if (m_nextFree)
{
tile = m_nextFree;
m_nextFree = tile->next;
tile->next = 0;
}
}
else
{
// Try to relocate the tile to specific index with same salt.
int tileIndex = (int)decodePolyIdTile((dtPolyRef)lastRef);
if (tileIndex >= m_maxTiles)
return DT_FAILURE | DT_OUT_OF_MEMORY;
// Try to find the specific tile id from the free list.
dtMeshTile* target = &m_tiles[tileIndex];
dtMeshTile* prev = 0;
tile = m_nextFree;
while (tile && tile != target)
{
prev = tile;
tile = tile->next;
}
// Could not find the correct location.
if (tile != target)
return DT_FAILURE | DT_OUT_OF_MEMORY;
// Remove from freelist
if (!prev)
m_nextFree = tile->next;
else
prev->next = tile->next;
// Restore salt.
tile->salt = decodePolyIdSalt((dtPolyRef)lastRef);
}
// Make sure we could allocate a tile.
if (!tile)
return DT_FAILURE | DT_OUT_OF_MEMORY;
// Insert tile into the position lut.
int h = computeTileHash(header->x, header->y, m_tileLutMask);
tile->next = m_posLookup[h];
m_posLookup[h] = tile;
// Patch header pointers.
const int headerSize = dtAlign4(sizeof(dtMeshHeader));
const int vertsSize = dtAlign4(sizeof(float)*3*header->vertCount);
const int polysSize = dtAlign4(sizeof(dtPoly)*header->polyCount);
const int linksSize = dtAlign4(sizeof(dtLink)*(header->maxLinkCount));
const int detailMeshesSize = dtAlign4(sizeof(dtPolyDetail)*header->detailMeshCount);
const int detailVertsSize = dtAlign4(sizeof(float)*3*header->detailVertCount);
const int detailTrisSize = dtAlign4(sizeof(unsigned char)*4*header->detailTriCount);
const int bvtreeSize = dtAlign4(sizeof(dtBVNode)*header->bvNodeCount);
const int offMeshLinksSize = dtAlign4(sizeof(dtOffMeshConnection)*header->offMeshConCount);
unsigned char* d = data + headerSize;
tile->verts = dtGetThenAdvanceBufferPointer<float>(d, vertsSize);
tile->polys = dtGetThenAdvanceBufferPointer<dtPoly>(d, polysSize);
tile->links = dtGetThenAdvanceBufferPointer<dtLink>(d, linksSize);
tile->detailMeshes = dtGetThenAdvanceBufferPointer<dtPolyDetail>(d, detailMeshesSize);
tile->detailVerts = dtGetThenAdvanceBufferPointer<float>(d, detailVertsSize);
tile->detailTris = dtGetThenAdvanceBufferPointer<unsigned char>(d, detailTrisSize);
tile->bvTree = dtGetThenAdvanceBufferPointer<dtBVNode>(d, bvtreeSize);
tile->offMeshCons = dtGetThenAdvanceBufferPointer<dtOffMeshConnection>(d, offMeshLinksSize);
// If there are no items in the bvtree, reset the tree pointer.
if (!bvtreeSize)
tile->bvTree = 0;
// Build links freelist
tile->linksFreeList = 0;
tile->links[header->maxLinkCount-1].next = DT_NULL_LINK;
for (int i = 0; i < header->maxLinkCount-1; ++i)
tile->links[i].next = i+1;
// Init tile.
tile->header = header;
tile->data = data;
tile->dataSize = dataSize;
tile->flags = flags;
connectIntLinks(tile);
// Base off-mesh connections to their starting polygons and connect connections inside the tile.
baseOffMeshLinks(tile);
connectExtOffMeshLinks(tile, tile, -1);
// Create connections with neighbour tiles.
static const int MAX_NEIS = 32;
dtMeshTile* neis[MAX_NEIS];
int nneis;
// Connect with layers in current tile.
nneis = getTilesAt(header->x, header->y, neis, MAX_NEIS);
for (int j = 0; j < nneis; ++j)
{
if (neis[j] == tile)
continue;
connectExtLinks(tile, neis[j], -1);
connectExtLinks(neis[j], tile, -1);
connectExtOffMeshLinks(tile, neis[j], -1);
connectExtOffMeshLinks(neis[j], tile, -1);
}
// Connect with neighbour tiles.
for (int i = 0; i < 8; ++i)
{
nneis = getNeighbourTilesAt(header->x, header->y, i, neis, MAX_NEIS);
for (int j = 0; j < nneis; ++j)
{
connectExtLinks(tile, neis[j], i);
connectExtLinks(neis[j], tile, dtOppositeTile(i));
connectExtOffMeshLinks(tile, neis[j], i);
connectExtOffMeshLinks(neis[j], tile, dtOppositeTile(i));
}
}
if (result)
*result = getTileRef(tile);
return DT_SUCCESS;
}
...
addTile的主要步骤为:- 根据
dtMeshHeader中的x、y、layer以及m_tileLutMask,在m_posLookup中查找对应的dtMeshTile对象,如果没有找到则取m_nextFree,并将导航网格数据存入dtMeshTile对象中。 - 将
tile->links[i].next初始化为i + 1。 - 通过
connectIntLinks方法,将每个多边形的顶点对应的邻居多边形信息,添加到tile->links中,并将首个dtLink存入到tile->polys[i]->firstLink中。 - 通过
baseOffMeshLinks方法,找到每个离网连接起始顶点的最近多边形,将最近多边形创建链接dtLink插入到离网连接起始顶点firstLink的头部,同时将离网连接起始顶点创建链接dtLink插入到最近多边形的firstLink的头部。 - 通过
connectExtOffMeshLinks方法,找到每个离网连接结束顶点的最近多边形,将最近多边形创建链接dtLink插入到离网连接结束顶点firstLink的头部,同时将离网连接结束顶点创建链接dtLink插入到最近多边形的firstLink的头部。 - 如果是多瓦片模式,则需要通过
connectExtLinks和connectExtOffMeshLinks方法,设置当前瓦片和邻居瓦片(其他层的同位置、相同层的邻居位置)的双向链接关系。
- 根据
- 初始化完成后,每个多边形的
firstLink则建立了一个dtLink链表,记录了所有邻居多边形的信息。
初始化导航网格查询
- 导航网格查询对象
dtNavMeshQuery的初始化方法如下:
// Detour/Source/DetourNavMeshQuery.cpp
...
dtStatus dtNavMeshQuery::init(const dtNavMesh* nav, const int maxNodes)
{
if (maxNodes > DT_NULL_IDX || maxNodes > (1 << DT_NODE_PARENT_BITS) - 1)
return DT_FAILURE | DT_INVALID_PARAM;
m_nav = nav;
if (!m_nodePool || m_nodePool->getMaxNodes() < maxNodes)
{
if (m_nodePool)
{
m_nodePool->~dtNodePool();
dtFree(m_nodePool);
m_nodePool = 0;
}
m_nodePool = new (dtAlloc(sizeof(dtNodePool), DT_ALLOC_PERM)) dtNodePool(maxNodes, dtNextPow2(maxNodes/4));
if (!m_nodePool)
return DT_FAILURE | DT_OUT_OF_MEMORY;
}
else
{
m_nodePool->clear();
}
if (!m_tinyNodePool)
{
m_tinyNodePool = new (dtAlloc(sizeof(dtNodePool), DT_ALLOC_PERM)) dtNodePool(64, 32);
if (!m_tinyNodePool)
return DT_FAILURE | DT_OUT_OF_MEMORY;
}
else
{
m_tinyNodePool->clear();
}
if (!m_openList || m_openList->getCapacity() < maxNodes)
{
if (m_openList)
{
m_openList->~dtNodeQueue();
dtFree(m_openList);
m_openList = 0;
}
m_openList = new (dtAlloc(sizeof(dtNodeQueue), DT_ALLOC_PERM)) dtNodeQueue(maxNodes);
if (!m_openList)
return DT_FAILURE | DT_OUT_OF_MEMORY;
}
else
{
m_openList->clear();
}
return DT_SUCCESS;
}
...
- 导航网格查询的初始化方法,主要就是对数据结构进行初始化,如节点对象池、开放列表等。初始化完成后,即可根据多边形的链接关系 (
dtPoly->firstLink和dtLink->next)使用查询对象进行寻路,即:dtNavMeshQuery::findNearestPoly查询点所在多边形。dtNavMeshQuery::findPath寻找最短多边形路径。dtNavMeshQuery::findStraightPath寻找最短路径。
总结
- 相比与寻路,导航网格的构建过程显得比较复杂,一个简单的瓦片网格需要经过八个步骤才能得到最终可以用于寻路的导航网格。通过了解导航网格的构建过程,在进行寻路处理时,能更加清楚其中的数据获取逻辑,进一步加深对寻路的理解。