Navmesh 寻路是游戏开发中常用的寻路算法，本文将基于 Recast Navigation 源码进行分析。
简介
- 以格子为基础的 A* 算法是游戏中最常用的寻路算法，随着游戏的发展，地图也在不断变化。随着地图的增大，A* 算法的开放列表也跟着增大，导致寻路效率已经达不到要求，因此出现了 JPS 算法进行改进。
- 相比传统网格地图寻路，导航网格（NavMesh）节点数量大幅减少，搜索空间缩小，能更快找到路径，在大规模复杂场景中优势明显，因此得到了广泛应用。
- Recast Navigation源码中，NavMesh 导航主要由两部分组成：
- Recast ：生成导航网格。
- Detour ：寻路。
- 在地图生成导航网格后，地图就拆分成众多形状各异的多边形，此时寻路的主要步骤为：
- 找到出发点和目标点所在的多边形。
- 找到一条最短的多边形路径。
- 从多边形路径中得到一条最短的路径。
查询点所在多边形
- 查询点所在多边形涉及的主要方法如下：
dtNavMeshQuery::findNearestPoly（查找点最近的多边形）
|——dtNavMeshQuery::queryPolygons（根据点和半径，查找最近的多边形）
|——dtNavMesh::getTilesAt（根据点查找所属的瓦片）
|——dtNavMeshQuery::queryPolygonsInTile（根据查询的最大最小范围，从瓦片的所有多边形中找到和查询点最近的多边形）
|——dtFindNearestPolyQuery::process（对一批多边形，查询其中和查询点最近的多边形）
|——dtNavMesh::closestPointOnPoly（在多边形中找到距离查询点最近的点，以及查询点是否在多边形 xz 投影平面内）
|——dtNavMesh::getPolyHeight（检查点是否在多边形投影平面内，以及点所在的三角面的高度）
|——dtDistancePtSegSqr2D（计算点到线段距离的平方）
|——closestPointOnDetailEdges（从细节边中找到和查询点最近的点）
dtNavMeshQuery::findNearestPoly
- 查询点所在多边形，主要通过
dtNavMeshQuery*对象的findNearestPoly方法实现，其代码如下：
// Detour/Source/DetourNavMeshQuery.cpp
...
dtStatus dtNavMeshQuery::findNearestPoly(const float* center, const float* halfExtents,
const dtQueryFilter* filter,
dtPolyRef* nearestRef, float* nearestPt) const
{
return findNearestPoly(center, halfExtents, filter, nearestRef, nearestPt, NULL);
}
dtStatus dtNavMeshQuery::findNearestPoly(const float* center, const float* halfExtents,
const dtQueryFilter* filter,
dtPolyRef* nearestRef, float* nearestPt, bool* isOverPoly) const
{
dtAssert(m_nav);
if (!nearestRef)
return DT_FAILURE | DT_INVALID_PARAM;
// queryPolygons below will check rest of params
dtFindNearestPolyQuery query(this, center);
dtStatus status = queryPolygons(center, halfExtents, filter, &query);
if (dtStatusFailed(status))
return status;
*nearestRef = query.nearestRef();
// Only override nearestPt if we actually found a poly so the nearest point
// is valid.
if (nearestPt && *nearestRef)
{
dtVcopy(nearestPt, query.nearestPoint());
if (isOverPoly)
*isOverPoly = query.isOverPoly();
}
return DT_SUCCESS;
}
...
- 创建一个
dtFindNearestPolyQuery的查询对象query，通过点的位置center和半径尺寸halfExtents，调用queryPolygons方法查询最近的多边形，找到了就将结果设置到nearestRef和nearestPt。
dtNavMeshQuery::queryPolygons
queryPolygons的实现如下：
// Detour/Source/DetourNavMeshQuery.cpp
...
dtStatus dtNavMeshQuery::queryPolygons(const float* center, const float* halfExtents,
const dtQueryFilter* filter, dtPolyQuery* query) const
{
dtAssert(m_nav);
if (!center || !dtVisfinite(center) ||
!halfExtents || !dtVisfinite(halfExtents) ||
!filter || !query)
{
return DT_FAILURE | DT_INVALID_PARAM;
}
float bmin[3], bmax[3];
dtVsub(bmin, center, halfExtents);
dtVadd(bmax, center, halfExtents);
// Find tiles the query touches.
int minx, miny, maxx, maxy;
m_nav->calcTileLoc(bmin, &minx, &miny);
m_nav->calcTileLoc(bmax, &maxx, &maxy);
static const int MAX_NEIS = 32;
const dtMeshTile* neis[MAX_NEIS];
for (int y = miny; y <= maxy; ++y)
{
for (int x = minx; x <= maxx; ++x)
{
const int nneis = m_nav->getTilesAt(x,y,neis,MAX_NEIS);
for (int j = 0; j < nneis; ++j)
{
queryPolygonsInTile(neis[j], bmin, bmax, filter, query);
}
}
}
return DT_SUCCESS;
}
...
- 查询的过程主要有以下步骤：
- 通过查询点
center和半径尺寸halfExtents的加减计算，得到要查询的范围大小。 - 通过
calTileLoc方法，将范围的x和z坐标转化为整数类型的瓦片坐标。 - 遍历所有瓦片坐标，通过
getTilesAt方法找到每一个坐标对应的所有瓦片对象。 - 对每一个瓦片对象，调用
queryPolygonsInTile方法查找最近的多边形。
- 通过查询点
dtNavMesh::getTilesAt
getTilesAt的方法如下：
// Detour/Source/DetourNavMesh.cpp
...
inline int computeTileHash(int x, int y, const int mask)
{
const unsigned int h1 = 0x8da6b343; // Large multiplicative constants;
const unsigned int h2 = 0xd8163841; // here arbitrarily chosen primes
unsigned int n = h1 * x + h2 * y;
return (int)(n & mask);
}
...
int dtNavMesh::getTilesAt(const int x, const int y, dtMeshTile const** tiles, const int maxTiles) const
{
int n = 0;
// Find tile based on hash.
int h = computeTileHash(x,y,m_tileLutMask);
dtMeshTile* tile = m_posLookup[h];
while (tile)
{
if (tile->header &&
tile->header->x == x &&
tile->header->y == y)
{
if (n < maxTiles)
tiles[n++] = tile;
}
tile = tile->next;
}
return n;
}
...
- 通过
computeTileHash方法计算哈希值，再通过m_posLookup数组找到对应的瓦片对象。如果坐标相同，则加入到瓦片对象数组中。其中h1和h2为两个任意选择的大素数，为了得到一个均匀分布的哈希值。
dtNavMeshQuery::queryPolygonsInTile
queryPolygonsInTile的实现如下：
// Detour/Source/DetourNavMeshQuery.cpp
...
void dtNavMeshQuery::queryPolygonsInTile(const dtMeshTile* tile, const float* qmin, const float* qmax,
const dtQueryFilter* filter, dtPolyQuery* query) const
{
dtAssert(m_nav);
static const int batchSize = 32;
dtPolyRef polyRefs[batchSize];
dtPoly* polys[batchSize];
int n = 0;
if (tile->bvTree)
{
const dtBVNode* node = &tile->bvTree[0];
const dtBVNode* end = &tile->bvTree[tile->header->bvNodeCount];
const float* tbmin = tile->header->bmin;
const float* tbmax = tile->header->bmax;
const float qfac = tile->header->bvQuantFactor;
// Calculate quantized box
unsigned short bmin[3], bmax[3];
// dtClamp query box to world box.
float minx = dtClamp(qmin[0], tbmin[0], tbmax[0]) - tbmin[0];
float miny = dtClamp(qmin[1], tbmin[1], tbmax[1]) - tbmin[1];
float minz = dtClamp(qmin[2], tbmin[2], tbmax[2]) - tbmin[2];
float maxx = dtClamp(qmax[0], tbmin[0], tbmax[0]) - tbmin[0];
float maxy = dtClamp(qmax[1], tbmin[1], tbmax[1]) - tbmin[1];
float maxz = dtClamp(qmax[2], tbmin[2], tbmax[2]) - tbmin[2];
// Quantize
bmin[0] = (unsigned short)(qfac * minx) & 0xfffe;
bmin[1] = (unsigned short)(qfac * miny) & 0xfffe;
bmin[2] = (unsigned short)(qfac * minz) & 0xfffe;
bmax[0] = (unsigned short)(qfac * maxx + 1) | 1;
bmax[1] = (unsigned short)(qfac * maxy + 1) | 1;
bmax[2] = (unsigned short)(qfac * maxz + 1) | 1;
// Traverse tree
const dtPolyRef base = m_nav->getPolyRefBase(tile);
while (node < end)
{
const bool overlap = dtOverlapQuantBounds(bmin, bmax, node->bmin, node->bmax);
const bool isLeafNode = node->i >= 0;
if (isLeafNode && overlap)
{
dtPolyRef ref = base | (dtPolyRef)node->i;
if (filter->passFilter(ref, tile, &tile->polys[node->i]))
{
polyRefs[n] = ref;
polys[n] = &tile->polys[node->i];
if (n == batchSize - 1)
{
query->process(tile, polys, polyRefs, batchSize);
n = 0;
}
else
{
n++;
}
}
}
if (overlap || isLeafNode)
node++;
else
{
const int escapeIndex = -node->i;
node += escapeIndex;
}
}
}
else
{
float bmin[3], bmax[3];
const dtPolyRef base = m_nav->getPolyRefBase(tile);
for (int i = 0; i < tile->header->polyCount; ++i)
{
dtPoly* p = &tile->polys[i];
// Do not return off-mesh connection polygons.
if (p->getType() == DT_POLYTYPE_OFFMESH_CONNECTION)
continue;
// Must pass filter
const dtPolyRef ref = base | (dtPolyRef)i;
if (!filter->passFilter(ref, tile, p))
continue;
// Calc polygon bounds.
const float* v = &tile->verts[p->verts[0]*3];
dtVcopy(bmin, v);
dtVcopy(bmax, v);
for (int j = 1; j < p->vertCount; ++j)
{
v = &tile->verts[p->verts[j]*3];
dtVmin(bmin, v);
dtVmax(bmax, v);
}
if (dtOverlapBounds(qmin, qmax, bmin, bmax))
{
polyRefs[n] = ref;
polys[n] = p;
if (n == batchSize - 1)
{
query->process(tile, polys, polyRefs, batchSize);
n = 0;
}
else
{
n++;
}
}
}
}
// Process the last polygons that didn't make a full batch.
if (n > 0)
query->process(tile, polys, polyRefs, n);
}
...
queryPolygonsInTile的主要步骤为：- 对瓦片中的每个多边形，计算其包围盒，判断是否与查询的区域相交。
- 如果瓦片采用了 BVH 结构管理，则仅需要查找和查询区域相交的子树。
- 对于相交的多边形，如果通过了过滤器，则加入到
polyRefs和polys中。 - 当累计多边形数量达到
batchSize时，调用query->process方法进行批处理。
dtFindNearestPolyQuery::process
query->process方法的实现如下：
// Detour/Source/DetourNavMeshQuery.cpp
...
class dtFindNearestPolyQuery : public dtPolyQuery
{
...
void process(const dtMeshTile* tile, dtPoly** polys, dtPolyRef* refs, int count)
{
dtIgnoreUnused(polys);
for (int i = 0; i < count; ++i)
{
dtPolyRef ref = refs[i];
float closestPtPoly[3];
float diff[3];
bool posOverPoly = false;
float d;
m_query->closestPointOnPoly(ref, m_center, closestPtPoly, &posOverPoly);
// If a point is directly over a polygon and closer than
// climb height, favor that instead of straight line nearest point.
dtVsub(diff, m_center, closestPtPoly);
if (posOverPoly)
{
d = dtAbs(diff[1]) - tile->header->walkableClimb;
d = d > 0 ? d*d : 0;
}
else
{
d = dtVlenSqr(diff);
}
if (d < m_nearestDistanceSqr)
{
dtVcopy(m_nearestPoint, closestPtPoly);
m_nearestDistanceSqr = d;
m_nearestRef = ref;
m_overPoly = posOverPoly;
}
}
}
};
...
process的主要步骤为：- 通过
closestPointOnPoly方法计算每一个多边形上和查询点距离最近的点closestPtPoly，且检查查询点是否在多边形的xz投影平面上。 - 计算最近点到查询点的向量差。
- 如果查询点在多边形的
xz投影平面上，则查询点和最近点的距离d计算方式为：- 如果向量差的垂直距离
y不大于瓦片的可行走高度walkableClimb，则查询点和最近点的距离d为 0 。 - 如果向量差的垂直距离
y大于瓦片的可行走高度walkableClimb，则查询点和最近点的距离d为超过部分的平方。
- 如果向量差的垂直距离
- 如果查询点不在多边形的
xz投影平面上，则查询点和最近点的距离为向量差的长度平方。 - 如果距离
d比当前最近距离m_nearestDistanceSqr小，则更新最近距离和最近多边形。
- 通过
dtNavMesh::closestPointOnPoly
closestPointOnPoly方法的实现如下：
// Detour/Source/DetourNavMesh.cpp
...
void dtNavMesh::closestPointOnPoly(dtPolyRef ref, const float* pos, float* closest, bool* posOverPoly) const
{
const dtMeshTile* tile = 0;
const dtPoly* poly = 0;
getTileAndPolyByRefUnsafe(ref, &tile, &poly);
dtVcopy(closest, pos);
if (getPolyHeight(tile, poly, pos, &closest[1]))
{
if (posOverPoly)
*posOverPoly = true;
return;
}
if (posOverPoly)
*posOverPoly = false;
// Off-mesh connections don't have detail polygons.
if (poly->getType() == DT_POLYTYPE_OFFMESH_CONNECTION)
{
const float* v0 = &tile->verts[poly->verts[0]*3];
const float* v1 = &tile->verts[poly->verts[1]*3];
float t;
dtDistancePtSegSqr2D(pos, v0, v1, t);
dtVlerp(closest, v0, v1, t);
return;
}
// Outside poly that is not an offmesh connection.
closestPointOnDetailEdges<true>(tile, poly, pos, closest);
}
...
- 查找多边形最近的点，主要分几类：
- 查询点在多边形的
xz投影平面区域，通过getPolyHeight计算。 - 查询点不在多边形的
xz投影平面区域的网格外连接（Off-mesh connections，即不直接连接的区域），通过dtDistancePtSegSqr2D计算距离，再插值得到最近点。 - 查询点不在多边形的
xz投影平面区域的非网格外连接，通过closestPointOnDetailEdges计算。
- 查询点在多边形的
dtNavMesh::getPolyHeight
getPolyHeight的实现如下：
// Detour/Source/DetourNavMesh.cpp
...
bool dtNavMesh::getPolyHeight(const dtMeshTile* tile, const dtPoly* poly, const float* pos, float* height) const
{
// Off-mesh connections do not have detail polys and getting height
// over them does not make sense.
if (poly->getType() == DT_POLYTYPE_OFFMESH_CONNECTION)
return false;
const unsigned int ip = (unsigned int)(poly - tile->polys);
const dtPolyDetail* pd = &tile->detailMeshes[ip];
float verts[DT_VERTS_PER_POLYGON*3];
const int nv = poly->vertCount;
for (int i = 0; i < nv; ++i)
dtVcopy(&verts[i*3], &tile->verts[poly->verts[i]*3]);
if (!dtPointInPolygon(pos, verts, nv))
return false;
if (!height)
return true;
// Find height at the location.
for (int j = 0; j < pd->triCount; ++j)
{
const unsigned char* t = &tile->detailTris[(pd->triBase+j)*4];
const float* v[3];
for (int k = 0; k < 3; ++k)
{
if (t[k] < poly->vertCount)
v[k] = &tile->verts[poly->verts[t[k]]*3];
else
v[k] = &tile->detailVerts[(pd->vertBase+(t[k]-poly->vertCount))*3];
}
float h;
if (dtClosestHeightPointTriangle(pos, v[0], v[1], v[2], h))
{
*height = h;
return true;
}
}
// If all triangle checks failed above (can happen with degenerate triangles
// or larger floating point values) the point is on an edge, so just select
// closest. This should almost never happen so the extra iteration here is
// ok.
float closest[3];
closestPointOnDetailEdges<false>(tile, poly, pos, closest);
*height = closest[1];
return true;
}
...
- 首先，通过
dtPointInPolygon方法，检查查询点是否在多边形的xz投影平面上。
// Detour/Source/DetourCommon.cpp
...
bool dtPointInPolygon(const float* pt, const float* verts, const int nverts)
{
// TODO: Replace pnpoly with triArea2D tests?
int i, j;
bool c = false;
for (i = 0, j = nverts-1; i < nverts; j = i++)
{
const float* vi = &verts[i*3];
const float* vj = &verts[j*3];
if (((vi[2] > pt[2]) != (vj[2] > pt[2])) &&
(pt[0] < (vj[0]-vi[0]) * (pt[2]-vi[2]) / (vj[2]-vi[2]) + vi[0]) )
c = !c;
}
return c;
}
...
- 遍历多边形的每条边，当查询点的
z坐标在边的z坐标范围内，且从查询点沿x轴正方向的射线和多边形的交点为奇数，则查询点在多边形内（射线法）。计算交点的方式为：- 计算边
ij上，当z坐标为pt[2]时的x坐标pt'[0]，即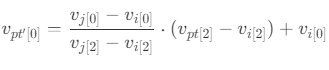
- 如果
pt'[0] > pt[0]，则表示射线与多边形有交点。
- 计算边
- 确定查询点在多边形投影面上后，则遍历多边形的每个三角面，通过
dtClosestHeightPointTriangle方法检查查询点所属的三角面投影面。
// Detour/Source/DetourCommon.cpp
...
bool dtClosestHeightPointTriangle(const float* p, const float* a, const float* b, const float* c, float& h)
{
const float EPS = 1e-6f;
float v0[3], v1[3], v2[3];
dtVsub(v0, c, a);
dtVsub(v1, b, a);
dtVsub(v2, p, a);
// Compute scaled barycentric coordinates
float denom = v0[0] * v1[2] - v0[2] * v1[0];
if (fabsf(denom) < EPS)
return false;
float u = v1[2] * v2[0] - v1[0] * v2[2];
float v = v0[0] * v2[2] - v0[2] * v2[0];
if (denom < 0) {
denom = -denom;
u = -u;
v = -v;
}
// If point lies inside the triangle, return interpolated ycoord.
if (u >= 0.0f && v >= 0.0f && (u + v) <= denom) {
h = a[1] + (v0[1] * u + v1[1] * v) / denom;
return true;
}
return false;
}
...
- 对于一个三角形
abc，先通过向量ac和ab的叉乘得到投影面上的面积（2倍），太小的直接剔除，再计算三角形abp和acp对应的面积。 - 如果
abp和acp的面积同为正或负，且面积和不超过abc，则表示点p在三角形abc内。 - 对于三角形内的任意一点
p，可以表示为三个顶点的线性组合，即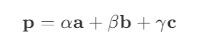
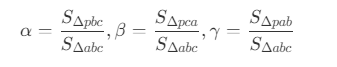因此通过插值可以得到点 p的y坐标。 - 如果查询点没有找到归属的三角面，则需要通过
closestPointOnDetailEdges方法计算最近点。 - 由于查询点在多边形投影面上，所以最近点的
xz坐标和查询点相同，仅计算垂直距离。
dtDistancePtSegSqr2D
dtDistancePtSegSqr2D用于计算查询点pt到线段pq的距离（平方值），其实现如下：
// Detour/Source/DetourCommon.cpp
...
float dtDistancePtSegSqr2D(const float* pt, const float* p, const float* q, float& t)
{
float pqx = q[0] - p[0];
float pqz = q[2] - p[2];
float dx = pt[0] - p[0];
float dz = pt[2] - p[2];
float d = pqx*pqx + pqz*pqz;
t = pqx*dx + pqz*dz;
if (d > 0) t /= d;
if (t < 0) t = 0;
else if (t > 1) t = 1;
dx = p[0] + t*pqx - pt[0];
dz = p[2] + t*pqz - pt[2];
return dx*dx + dz*dz;
}
...
- 主要思路是，计算点
pt在线段pq上的投影位置，然后计算该位置到点pt的距离，即为查询点到线段pq的距离。投影位置的长度为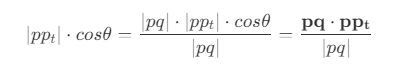
- 投影点在线段
pq上的比例为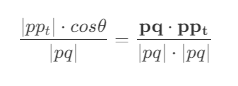
- 因此投影点的坐标可以通过比例和点
p坐标插值计算得到，从而可以得到查询点到线段的距离。
closestPointOnDetailEdges
closestPointOnDetailEdges用于计算细节边到查询点的最近点，其实现如下：
// Detour/Source/DetourNavMesh.cpp
...
template<bool onlyBoundary>
void closestPointOnDetailEdges(const dtMeshTile* tile, const dtPoly* poly, const float* pos, float* closest)
{
const unsigned int ip = (unsigned int)(poly - tile->polys);
const dtPolyDetail* pd = &tile->detailMeshes[ip];
float dmin = FLT_MAX;
float tmin = 0;
const float* pmin = 0;
const float* pmax = 0;
for (int i = 0; i < pd->triCount; i++)
{
const unsigned char* tris = &tile->detailTris[(pd->triBase + i) * 4];
const int ANY_BOUNDARY_EDGE =
(DT_DETAIL_EDGE_BOUNDARY << 0) |
(DT_DETAIL_EDGE_BOUNDARY << 2) |
(DT_DETAIL_EDGE_BOUNDARY << 4);
if (onlyBoundary && (tris[3] & ANY_BOUNDARY_EDGE) == 0)
continue;
const float* v[3];
for (int j = 0; j < 3; ++j)
{
if (tris[j] < poly->vertCount)
v[j] = &tile->verts[poly->verts[tris[j]] * 3];
else
v[j] = &tile->detailVerts[(pd->vertBase + (tris[j] - poly->vertCount)) * 3];
}
for (int k = 0, j = 2; k < 3; j = k++)
{
if ((dtGetDetailTriEdgeFlags(tris[3], j) & DT_DETAIL_EDGE_BOUNDARY) == 0 &&
(onlyBoundary || tris[j] < tris[k]))
{
// Only looking at boundary edges and this is internal, or
// this is an inner edge that we will see again or have already seen.
continue;
}
float t;
float d = dtDistancePtSegSqr2D(pos, v[j], v[k], t);
if (d < dmin)
{
dmin = d;
tmin = t;
pmin = v[j];
pmax = v[k];
}
}
}
dtVlerp(closest, pmin, pmax, tmin);
}
...
- 在细节边上找最近点，使用的也是
dtDistancePtSegSqr2D方法。对多个细节边上的最近点，取投影距离最小的点作为最终的最近点。
寻找最短多边形路径
- 寻找最短多边形路径涉及的主要方法如下：
dtNavMeshQuery::findPath（查找多边形路径）
|——dtNavMeshQuery::getEdgeMidPoint（计算共享边的中点位置）
| |——dtNavMeshQuery::getPortalPoints（计算多边形共享边的左右顶点）
|——dtQueryFilter::getCost（计算两个点之间的代价）
|——dtNavMeshQuery::getPathToNode（将节点转化为一条路径）
dtNavMeshQuery::findPath
findPath的实现如下：
// Detour/Source/DetourNavMeshQuery.cpp
...
dtStatus dtNavMeshQuery::findPath(dtPolyRef startRef, dtPolyRef endRef,
const float* startPos, const float* endPos,
const dtQueryFilter* filter,
dtPolyRef* path, int* pathCount, const int maxPath) const
{
dtAssert(m_nav);
dtAssert(m_nodePool);
dtAssert(m_openList);
if (!pathCount)
return DT_FAILURE | DT_INVALID_PARAM;
*pathCount = 0;
// Validate input
if (!m_nav->isValidPolyRef(startRef) || !m_nav->isValidPolyRef(endRef) ||
!startPos || !dtVisfinite(startPos) ||
!endPos || !dtVisfinite(endPos) ||
!filter || !path || maxPath <= 0)
{
return DT_FAILURE | DT_INVALID_PARAM;
}
if (startRef == endRef)
{
path[0] = startRef;
*pathCount = 1;
return DT_SUCCESS;
}
m_nodePool->clear();
m_openList->clear();
dtNode* startNode = m_nodePool->getNode(startRef);
dtVcopy(startNode->pos, startPos);
startNode->pidx = 0;
startNode->cost = 0;
startNode->total = dtVdist(startPos, endPos) * H_SCALE;
startNode->id = startRef;
startNode->flags = DT_NODE_OPEN;
m_openList->push(startNode);
dtNode* lastBestNode = startNode;
float lastBestNodeCost = startNode->total;
bool outOfNodes = false;
while (!m_openList->empty())
{
// Remove node from open list and put it in closed list.
dtNode* bestNode = m_openList->pop();
bestNode->flags &= ~DT_NODE_OPEN;
bestNode->flags |= DT_NODE_CLOSED;
// Reached the goal, stop searching.
if (bestNode->id == endRef)
{
lastBestNode = bestNode;
break;
}
// Get current poly and tile.
// The API input has been checked already, skip checking internal data.
const dtPolyRef bestRef = bestNode->id;
const dtMeshTile* bestTile = 0;
const dtPoly* bestPoly = 0;
m_nav->getTileAndPolyByRefUnsafe(bestRef, &bestTile, &bestPoly);
// Get parent poly and tile.
dtPolyRef parentRef = 0;
const dtMeshTile* parentTile = 0;
const dtPoly* parentPoly = 0;
if (bestNode->pidx)
parentRef = m_nodePool->getNodeAtIdx(bestNode->pidx)->id;
if (parentRef)
m_nav->getTileAndPolyByRefUnsafe(parentRef, &parentTile, &parentPoly);
for (unsigned int i = bestPoly->firstLink; i != DT_NULL_LINK; i = bestTile->links[i].next)
{
dtPolyRef neighbourRef = bestTile->links[i].ref;
// Skip invalid ids and do not expand back to where we came from.
if (!neighbourRef || neighbourRef == parentRef)
continue;
// Get neighbour poly and tile.
// The API input has been checked already, skip checking internal data.
const dtMeshTile* neighbourTile = 0;
const dtPoly* neighbourPoly = 0;
m_nav->getTileAndPolyByRefUnsafe(neighbourRef, &neighbourTile, &neighbourPoly);
if (!filter->passFilter(neighbourRef, neighbourTile, neighbourPoly))
continue;
// deal explicitly with crossing tile boundaries
unsigned char crossSide = 0;
if (bestTile->links[i].side != 0xff)
crossSide = bestTile->links[i].side >> 1;
// get the node
dtNode* neighbourNode = m_nodePool->getNode(neighbourRef, crossSide);
if (!neighbourNode)
{
outOfNodes = true;
continue;
}
// If the node is visited the first time, calculate node position.
if (neighbourNode->flags == 0)
{
getEdgeMidPoint(bestRef, bestPoly, bestTile,
neighbourRef, neighbourPoly, neighbourTile,
neighbourNode->pos);
}
// Calculate cost and heuristic.
float cost = 0;
float heuristic = 0;
// Special case for last node.
if (neighbourRef == endRef)
{
// Cost
const float curCost = filter->getCost(bestNode->pos, neighbourNode->pos,
parentRef, parentTile, parentPoly,
bestRef, bestTile, bestPoly,
neighbourRef, neighbourTile, neighbourPoly);
const float endCost = filter->getCost(neighbourNode->pos, endPos,
bestRef, bestTile, bestPoly,
neighbourRef, neighbourTile, neighbourPoly,
0, 0, 0);
cost = bestNode->cost + curCost + endCost;
heuristic = 0;
}
else
{
// Cost
const float curCost = filter->getCost(bestNode->pos, neighbourNode->pos,
parentRef, parentTile, parentPoly,
bestRef, bestTile, bestPoly,
neighbourRef, neighbourTile, neighbourPoly);
cost = bestNode->cost + curCost;
heuristic = dtVdist(neighbourNode->pos, endPos)*H_SCALE;
}
const float total = cost + heuristic;
// The node is already in open list and the new result is worse, skip.
if ((neighbourNode->flags & DT_NODE_OPEN) && total >= neighbourNode->total)
continue;
// The node is already visited and process, and the new result is worse, skip.
if ((neighbourNode->flags & DT_NODE_CLOSED) && total >= neighbourNode->total)
continue;
// Add or update the node.
neighbourNode->pidx = m_nodePool->getNodeIdx(bestNode);
neighbourNode->id = neighbourRef;
neighbourNode->flags = (neighbourNode->flags & ~DT_NODE_CLOSED);
neighbourNode->cost = cost;
neighbourNode->total = total;
if (neighbourNode->flags & DT_NODE_OPEN)
{
// Already in open, update node location.
m_openList->modify(neighbourNode);
}
else
{
// Put the node in open list.
neighbourNode->flags |= DT_NODE_OPEN;
m_openList->push(neighbourNode);
}
// Update nearest node to target so far.
if (heuristic < lastBestNodeCost)
{
lastBestNodeCost = heuristic;
lastBestNode = neighbourNode;
}
}
}
dtStatus status = getPathToNode(lastBestNode, path, pathCount, maxPath);
if (lastBestNode->id != endRef)
status |= DT_PARTIAL_RESULT;
if (outOfNodes)
status |= DT_OUT_OF_NODES;
return status;
}
...
findPath寻路方法核心为 A* 算法，主要步骤如下：- 初始化节点对象池
m_nodePool和开放列表m_openList。 - 从节点对象池中获取起点多边形的节点，设置节点的信息，包括：
- 父节点 id ：
pidx。 - 当前节点的代价：
cost。 - 总代价：
total。 - 节点 id ：
id。 - 节点访问标记：
flags。
- 父节点 id ：
- 将起始节点加入开放列表中。
- 从开放列表中取出一个节点，对节点做检查。
- 如果节点为终点，则结束处理。
- 遍历节点所在多边形的每一个共享边，找到共享边对应的邻居多边形。
- 根据邻居多边形的 id 和共享边，从节点对象池中获取邻居节点。
- 通过
getEdgeMidPoint方法，计算邻居节点的位置（共享边的中点）。 - 通过
getCost方法，计算当前节点到邻居节点的代价。 - 计算邻居节点的位置和目标位置的距离，乘上
H_SCALE系数，作为启发式预估代价。 - 总代价为当前代价和预估代价之和。
- 更新邻居节点的信息。
- 将邻居节点加入开放列表中。
- 比较邻居节点和最近节点的预估代价，如果邻居节点的预估代价更小，则更新最近节点为邻居节点。
- 从开放列表中取下一个节点，继续上述处理。
- 通过
getPathToNode方法，将最近节点进行递归，得到最终路径。
- 初始化节点对象池
dtNavMeshQuery::getEdgeMidPoint
getEdgeMidPoint的实现如下：
// Detour/Source/DetourNavMeshQuery.cpp
...
dtStatus dtNavMeshQuery::getEdgeMidPoint(dtPolyRef from, const dtPoly* fromPoly, const dtMeshTile* fromTile,
dtPolyRef to, const dtPoly* toPoly, const dtMeshTile* toTile,
float* mid) const
{
float left[3], right[3];
if (dtStatusFailed(getPortalPoints(from, fromPoly, fromTile, to, toPoly, toTile, left, right)))
return DT_FAILURE | DT_INVALID_PARAM;
mid[0] = (left[0]+right[0])*0.5f;
mid[1] = (left[1]+right[1])*0.5f;
mid[2] = (left[2]+right[2])*0.5f;
return DT_SUCCESS;
}
...
- 通过
getPortalPoints方法，计算两个多边形共享边的左右顶点，根据左右顶点计算共享边的中点。
dtNavMeshQuery::getPortalPoints
getPortalPoints的实现如下：
// Detour/Source/DetourNavMeshQuery.cpp
...
dtStatus dtNavMeshQuery::getPortalPoints(dtPolyRef from, const dtPoly* fromPoly, const dtMeshTile* fromTile,
dtPolyRef to, const dtPoly* toPoly, const dtMeshTile* toTile,
float* left, float* right) const
{
// Find the link that points to the 'to' polygon.
const dtLink* link = 0;
for (unsigned int i = fromPoly->firstLink; i != DT_NULL_LINK; i = fromTile->links[i].next)
{
if (fromTile->links[i].ref == to)
{
link = &fromTile->links[i];
break;
}
}
if (!link)
return DT_FAILURE | DT_INVALID_PARAM;
// Handle off-mesh connections.
if (fromPoly->getType() == DT_POLYTYPE_OFFMESH_CONNECTION)
{
// Find link that points to first vertex.
for (unsigned int i = fromPoly->firstLink; i != DT_NULL_LINK; i = fromTile->links[i].next)
{
if (fromTile->links[i].ref == to)
{
const int v = fromTile->links[i].edge;
dtVcopy(left, &fromTile->verts[fromPoly->verts[v]*3]);
dtVcopy(right, &fromTile->verts[fromPoly->verts[v]*3]);
return DT_SUCCESS;
}
}
return DT_FAILURE | DT_INVALID_PARAM;
}
if (toPoly->getType() == DT_POLYTYPE_OFFMESH_CONNECTION)
{
for (unsigned int i = toPoly->firstLink; i != DT_NULL_LINK; i = toTile->links[i].next)
{
if (toTile->links[i].ref == from)
{
const int v = toTile->links[i].edge;
dtVcopy(left, &toTile->verts[toPoly->verts[v]*3]);
dtVcopy(right, &toTile->verts[toPoly->verts[v]*3]);
return DT_SUCCESS;
}
}
return DT_FAILURE | DT_INVALID_PARAM;
}
// Find portal vertices.
const int v0 = fromPoly->verts[link->edge];
const int v1 = fromPoly->verts[(link->edge+1) % (int)fromPoly->vertCount];
dtVcopy(left, &fromTile->verts[v0*3]);
dtVcopy(right, &fromTile->verts[v1*3]);
// If the link is at tile boundary, dtClamp the vertices to
// the link width.
if (link->side != 0xff)
{
// Unpack portal limits.
if (link->bmin != 0 || link->bmax != 255)
{
const float s = 1.0f/255.0f;
const float tmin = link->bmin*s;
const float tmax = link->bmax*s;
dtVlerp(left, &fromTile->verts[v0*3], &fromTile->verts[v1*3], tmin);
dtVlerp(right, &fromTile->verts[v0*3], &fromTile->verts[v1*3], tmax);
}
}
return DT_SUCCESS;
}
...
- 对于网格外连接，则遍历多边形的所有连接，找到连接多边形的边，其左右顶点都为该顶点。
- 对于非网格外连接，则连接边的首顶点为左顶点，尾顶点为右顶点。
dtQueryFilter::getCost
getCost的实现如下：
// Detour/Source/DetourNavMeshQuery.cpp
...
inline float dtQueryFilter::getCost(const float* pa, const float* pb,
const dtPolyRef /*prevRef*/, const dtMeshTile* /*prevTile*/, const dtPoly* /*prevPoly*/,
const dtPolyRef /*curRef*/, const dtMeshTile* /*curTile*/, const dtPoly* curPoly,
const dtPolyRef /*nextRef*/, const dtMeshTile* /*nextTile*/, const dtPoly* /*nextPoly*/) const
{
return dtVdist(pa, pb) * m_areaCost[curPoly->getArea()];
}
...
- 两个点的代价，为两点之间的距离，乘上当前多边形所属区域对应的区域代价。
dtNavMeshQuery::getPathToNode
getPathToNode的实现如下：
// Detour/Source/DetourNavMeshQuery.cpp
...
dtStatus dtNavMeshQuery::getPathToNode(dtNode* endNode, dtPolyRef* path, int* pathCount, int maxPath) const
{
// Find the length of the entire path.
dtNode* curNode = endNode;
int length = 0;
do
{
length++;
curNode = m_nodePool->getNodeAtIdx(curNode->pidx);
} while (curNode);
// If the path cannot be fully stored then advance to the last node we will be able to store.
curNode = endNode;
int writeCount;
for (writeCount = length; writeCount > maxPath; writeCount--)
{
dtAssert(curNode);
curNode = m_nodePool->getNodeAtIdx(curNode->pidx);
}
// Write path
for (int i = writeCount - 1; i >= 0; i--)
{
dtAssert(curNode);
path[i] = curNode->id;
curNode = m_nodePool->getNodeAtIdx(curNode->pidx);
}
dtAssert(!curNode);
*pathCount = dtMin(length, maxPath);
if (length > maxPath)
return DT_SUCCESS | DT_BUFFER_TOO_SMALL;
return DT_SUCCESS;
}
...
- 当寻路找到目标节点后，需要找到完整的路径。通过递归获取节点的父节点，则可以得到一条从起始点出发的完整路径。
寻找最短路径
- 通过上一步的寻路，可以得到一条多边形路径，从起始点开始，经过每一条共享边的中点，直到目标点，如图所示：
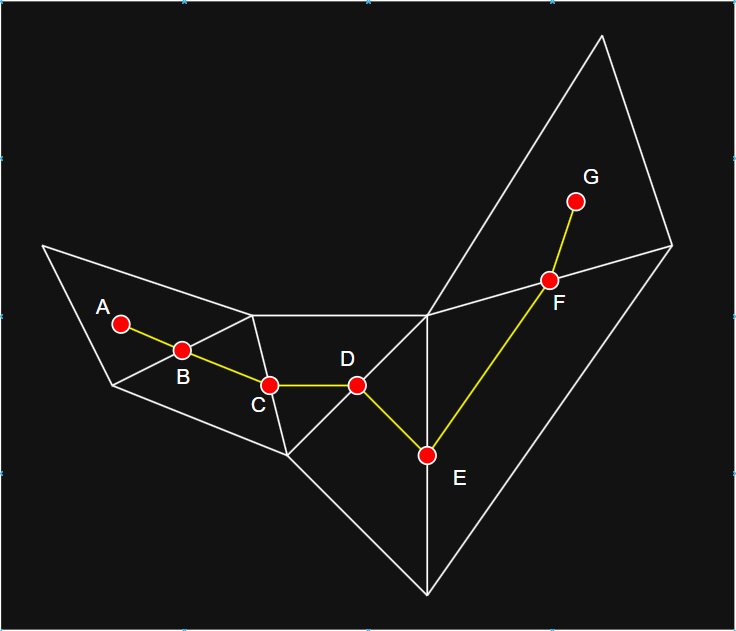
- 可以看到，尽管找到了一条路径，但可以发现，如果沿着路径 A ~ G 前进，并不是最短路径，所以还需要通过
findStraightPath方法进一步进行路径优化，该方法通常称为拉绳算法或漏斗算法。 - 寻找最短路径涉及的主要方法如下：
dtNavMeshQuery::findStraightPath（根据多边形路径，计算最短直线路径）
|——dtNavMeshQuery::closestPointOnPolyBoundary（计算点在多边形上的最近点）
|——dtNavMeshQuery::appendVertex（将点加入到直线路径列表）
|——dtNavMeshQuery::getPortalPoints（计算多边形共享边的左右顶点）
|——dtTriArea2D（计算向量 AC 和 AB 的叉积，确定 C 点在 AB 的左侧还是右侧）
|——dtNavMeshQuery::appendPortals
dtNavMeshQuery::findStraightPath
findStraightPath的实现如下：
// Detour/Source/DetourNavMeshQuery.cpp
...
dtStatus dtNavMeshQuery::findStraightPath(const float* startPos, const float* endPos,
const dtPolyRef* path, const int pathSize,
float* straightPath, unsigned char* straightPathFlags, dtPolyRef* straightPathRefs,
int* straightPathCount, const int maxStraightPath, const int options) const
{
dtAssert(m_nav);
if (!straightPathCount)
return DT_FAILURE | DT_INVALID_PARAM;
*straightPathCount = 0;
if (!startPos || !dtVisfinite(startPos) ||
!endPos || !dtVisfinite(endPos) ||
!path || pathSize <= 0 || !path[0] ||
maxStraightPath <= 0)
{
return DT_FAILURE | DT_INVALID_PARAM;
}
dtStatus stat = 0;
// TODO: Should this be callers responsibility?
float closestStartPos[3];
if (dtStatusFailed(closestPointOnPolyBoundary(path[0], startPos, closestStartPos)))
return DT_FAILURE | DT_INVALID_PARAM;
float closestEndPos[3];
if (dtStatusFailed(closestPointOnPolyBoundary(path[pathSize-1], endPos, closestEndPos)))
return DT_FAILURE | DT_INVALID_PARAM;
// Add start point.
stat = appendVertex(closestStartPos, DT_STRAIGHTPATH_START, path[0],
straightPath, straightPathFlags, straightPathRefs,
straightPathCount, maxStraightPath);
if (stat != DT_IN_PROGRESS)
return stat;
if (pathSize > 1)
{
float portalApex[3], portalLeft[3], portalRight[3];
dtVcopy(portalApex, closestStartPos);
dtVcopy(portalLeft, portalApex);
dtVcopy(portalRight, portalApex);
int apexIndex = 0;
int leftIndex = 0;
int rightIndex = 0;
unsigned char leftPolyType = 0;
unsigned char rightPolyType = 0;
dtPolyRef leftPolyRef = path[0];
dtPolyRef rightPolyRef = path[0];
for (int i = 0; i < pathSize; ++i)
{
float left[3], right[3];
unsigned char toType;
if (i+1 < pathSize)
{
unsigned char fromType; // fromType is ignored.
// Next portal.
if (dtStatusFailed(getPortalPoints(path[i], path[i+1], left, right, fromType, toType)))
{
// Failed to get portal points, in practice this means that path[i+1] is invalid polygon.
// Clamp the end point to path[i], and return the path so far.
if (dtStatusFailed(closestPointOnPolyBoundary(path[i], endPos, closestEndPos)))
{
// This should only happen when the first polygon is invalid.
return DT_FAILURE | DT_INVALID_PARAM;
}
// Apeend portals along the current straight path segment.
if (options & (DT_STRAIGHTPATH_AREA_CROSSINGS | DT_STRAIGHTPATH_ALL_CROSSINGS))
{
// Ignore status return value as we're just about to return anyway.
appendPortals(apexIndex, i, closestEndPos, path,
straightPath, straightPathFlags, straightPathRefs,
straightPathCount, maxStraightPath, options);
}
// Ignore status return value as we're just about to return anyway.
appendVertex(closestEndPos, 0, path[i],
straightPath, straightPathFlags, straightPathRefs,
straightPathCount, maxStraightPath);
return DT_SUCCESS | DT_PARTIAL_RESULT | ((*straightPathCount >= maxStraightPath) ? DT_BUFFER_TOO_SMALL : 0);
}
// If starting really close the portal, advance.
if (i == 0)
{
float t;
if (dtDistancePtSegSqr2D(portalApex, left, right, t) < dtSqr(0.001f))
continue;
}
}
else
{
// End of the path.
dtVcopy(left, closestEndPos);
dtVcopy(right, closestEndPos);
toType = DT_POLYTYPE_GROUND;
}
// Right vertex.
if (dtTriArea2D(portalApex, portalRight, right) <= 0.0f)
{
if (dtVequal(portalApex, portalRight) || dtTriArea2D(portalApex, portalLeft, right) > 0.0f)
{
dtVcopy(portalRight, right);
rightPolyRef = (i+1 < pathSize) ? path[i+1] : 0;
rightPolyType = toType;
rightIndex = i;
}
else
{
// Append portals along the current straight path segment.
if (options & (DT_STRAIGHTPATH_AREA_CROSSINGS | DT_STRAIGHTPATH_ALL_CROSSINGS))
{
stat = appendPortals(apexIndex, leftIndex, portalLeft, path,
straightPath, straightPathFlags, straightPathRefs,
straightPathCount, maxStraightPath, options);
if (stat != DT_IN_PROGRESS)
return stat;
}
dtVcopy(portalApex, portalLeft);
apexIndex = leftIndex;
unsigned char flags = 0;
if (!leftPolyRef)
flags = DT_STRAIGHTPATH_END;
else if (leftPolyType == DT_POLYTYPE_OFFMESH_CONNECTION)
flags = DT_STRAIGHTPATH_OFFMESH_CONNECTION;
dtPolyRef ref = leftPolyRef;
// Append or update vertex
stat = appendVertex(portalApex, flags, ref,
straightPath, straightPathFlags, straightPathRefs,
straightPathCount, maxStraightPath);
if (stat != DT_IN_PROGRESS)
return stat;
dtVcopy(portalLeft, portalApex);
dtVcopy(portalRight, portalApex);
leftIndex = apexIndex;
rightIndex = apexIndex;
// Restart
i = apexIndex;
continue;
}
}
// Left vertex.
if (dtTriArea2D(portalApex, portalLeft, left) >= 0.0f)
{
if (dtVequal(portalApex, portalLeft) || dtTriArea2D(portalApex, portalRight, left) < 0.0f)
{
dtVcopy(portalLeft, left);
leftPolyRef = (i+1 < pathSize) ? path[i+1] : 0;
leftPolyType = toType;
leftIndex = i;
}
else
{
// Append portals along the current straight path segment.
if (options & (DT_STRAIGHTPATH_AREA_CROSSINGS | DT_STRAIGHTPATH_ALL_CROSSINGS))
{
stat = appendPortals(apexIndex, rightIndex, portalRight, path,
straightPath, straightPathFlags, straightPathRefs,
straightPathCount, maxStraightPath, options);
if (stat != DT_IN_PROGRESS)
return stat;
}
dtVcopy(portalApex, portalRight);
apexIndex = rightIndex;
unsigned char flags = 0;
if (!rightPolyRef)
flags = DT_STRAIGHTPATH_END;
else if (rightPolyType == DT_POLYTYPE_OFFMESH_CONNECTION)
flags = DT_STRAIGHTPATH_OFFMESH_CONNECTION;
dtPolyRef ref = rightPolyRef;
// Append or update vertex
stat = appendVertex(portalApex, flags, ref,
straightPath, straightPathFlags, straightPathRefs,
straightPathCount, maxStraightPath);
if (stat != DT_IN_PROGRESS)
return stat;
dtVcopy(portalLeft, portalApex);
dtVcopy(portalRight, portalApex);
leftIndex = apexIndex;
rightIndex = apexIndex;
// Restart
i = apexIndex;
continue;
}
}
}
// Append portals along the current straight path segment.
if (options & (DT_STRAIGHTPATH_AREA_CROSSINGS | DT_STRAIGHTPATH_ALL_CROSSINGS))
{
stat = appendPortals(apexIndex, pathSize-1, closestEndPos, path,
straightPath, straightPathFlags, straightPathRefs,
straightPathCount, maxStraightPath, options);
if (stat != DT_IN_PROGRESS)
return stat;
}
}
// Ignore status return value as we're just about to return anyway.
appendVertex(closestEndPos, DT_STRAIGHTPATH_END, 0,
straightPath, straightPathFlags, straightPathRefs,
straightPathCount, maxStraightPath);
return DT_SUCCESS | ((*straightPathCount >= maxStraightPath) ? DT_BUFFER_TOO_SMALL : 0);
}
...
- 根据已经找到的多边形路径，计算流程主要为：
- 通过
closestPointOnPolyBoundary方法，找到起始点和目标点在多边形上最近的点。 - 通过
appendVertex方法，将起始点加入到直线路径列表straightPath中。 - 设置绳子顶端点
portalApex、左侧绳子底部点portalLeft、右侧绳子底部点portalRight为起始点在多边形上的最近点。 - 遍历多边形路径列表处理：
- 获取和下一个多边形共享边的左右点。
- 通过
dtTriArea2D方法，检查共享边的右侧点的位置。- 如果共享边的右侧点的位置在两条绳子的夹角内（包括在右侧绳子上），则更新右侧绳子底部点为共享边右侧点。
- 如果共享边的右侧点的位置在两条绳子的左侧，则更新绳子顶端点为左侧绳子底部点，重置左右绳子的底部点为顶端点。
- 通过
dtTriArea2D方法检查共享边左侧点，右侧点的位置。- 如果共享边的左侧点的位置在两条绳子的夹角内（包括在左侧绳子上），则更新左侧绳子底部点为共享边左侧点。
- 如果共享边的左侧点的位置在两条绳子的左侧，则更新绳子顶端点为右侧绳子底部点，重置左右绳子的底部点为顶端点。
- 将目标点加入到直线路径列表中，得到最终路径。
- 通过
- 如图所示，A 为起始点，G 为目标点，S 为共享边，L 和 R 分别为左右两侧绳子底部点，L' 和 R' 为共享边左右侧点。
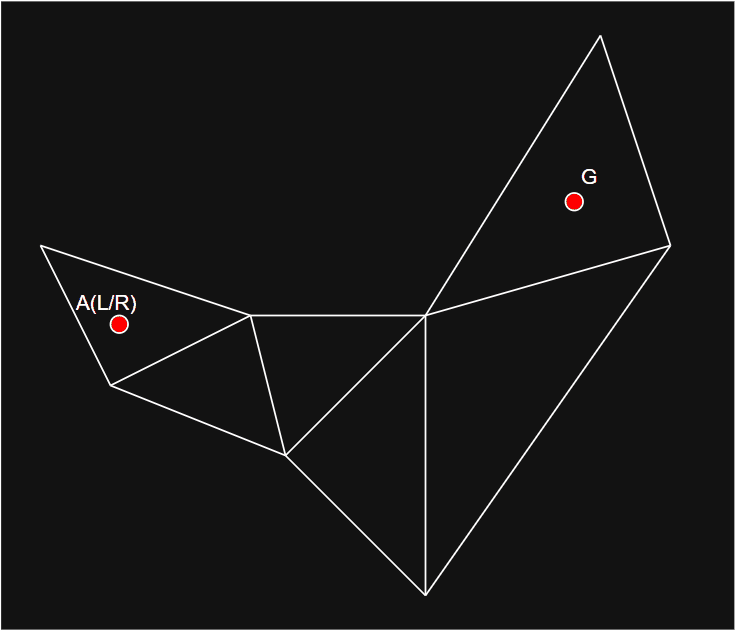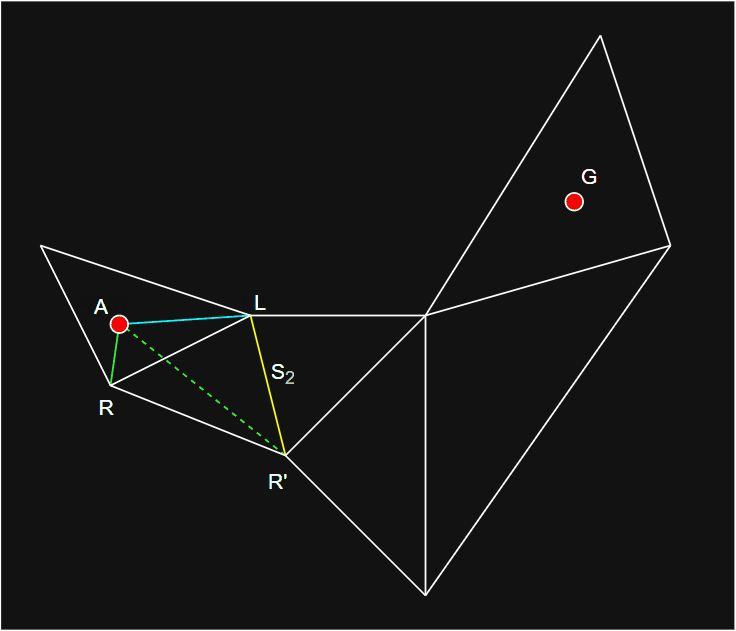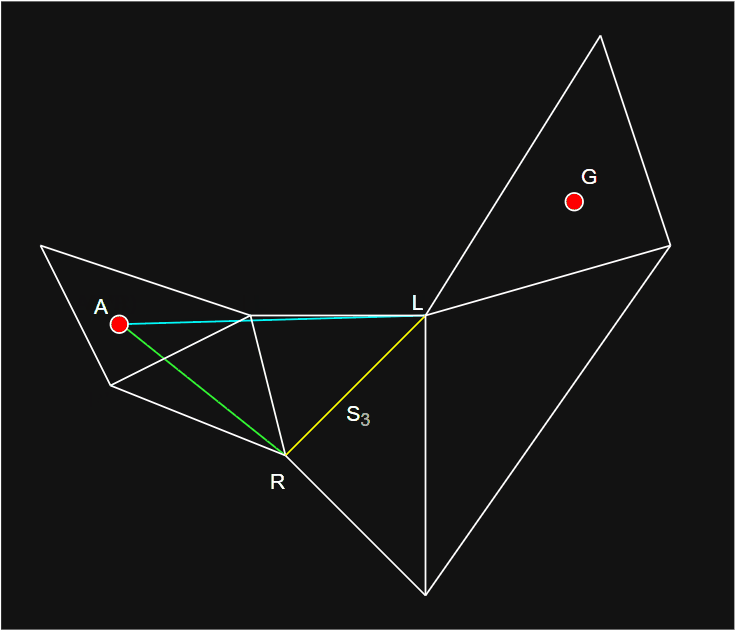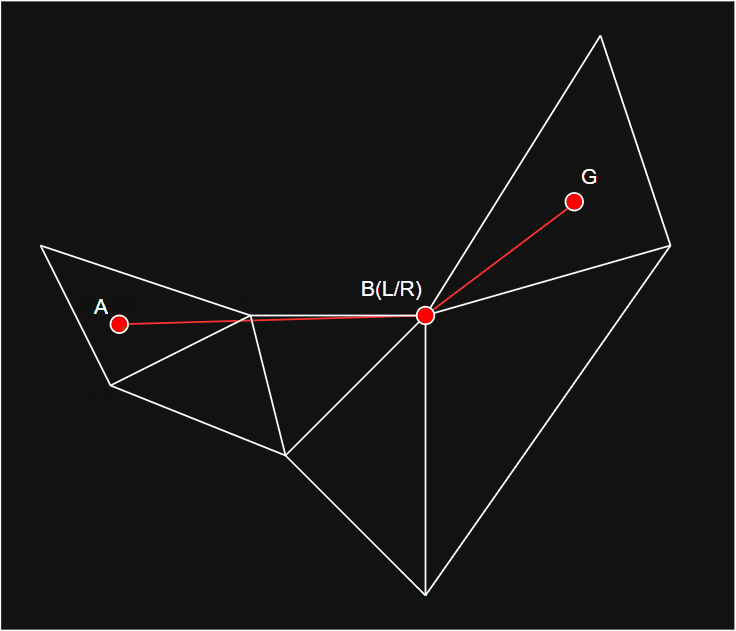
dtNavMeshQuery::closestPointOnPolyBoundary
closestPointOnPolyBoundary方法的实现如下：
// Detour/Source/DetourNavMeshQuery.cpp
...
dtStatus dtNavMeshQuery::closestPointOnPolyBoundary(dtPolyRef ref, const float* pos, float* closest) const
{
dtAssert(m_nav);
const dtMeshTile* tile = 0;
const dtPoly* poly = 0;
if (dtStatusFailed(m_nav->getTileAndPolyByRef(ref, &tile, &poly)))
return DT_FAILURE | DT_INVALID_PARAM;
if (!pos || !dtVisfinite(pos) || !closest)
return DT_FAILURE | DT_INVALID_PARAM;
// Collect vertices.
float verts[DT_VERTS_PER_POLYGON*3];
float edged[DT_VERTS_PER_POLYGON];
float edget[DT_VERTS_PER_POLYGON];
int nv = 0;
for (int i = 0; i < (int)poly->vertCount; ++i)
{
dtVcopy(&verts[nv*3], &tile->verts[poly->verts[i]*3]);
nv++;
}
bool inside = dtDistancePtPolyEdgesSqr(pos, verts, nv, edged, edget);
if (inside)
{
// Point is inside the polygon, return the point.
dtVcopy(closest, pos);
}
else
{
// Point is outside the polygon, dtClamp to nearest edge.
float dmin = edged[0];
int imin = 0;
for (int i = 1; i < nv; ++i)
{
if (edged[i] < dmin)
{
dmin = edged[i];
imin = i;
}
}
const float* va = &verts[imin*3];
const float* vb = &verts[((imin+1)%nv)*3];
dtVlerp(closest, va, vb, edget[imin]);
}
return DT_SUCCESS;
}
...
- 首先，通过
dtDistancePtPolyEdgesSqr方法，使用射线法检查目标点是否在多边形内，同时通过dtDistancePtSegSqr2D方法计算目标点到各条边的距离平方及投影比例。 - 如果目标点在多边形内，则最近点为目标点。
- 如果目标点在多边形外，则取离目标点最近的边，计算目标点在该边上的投影点则为最近点。
dtNavMeshQuery::appendVertex
appendVertex方法的实现如下：
// Detour/Source/DetourNavMeshQuery.cpp
...
dtStatus dtNavMeshQuery::appendVertex(const float* pos, const unsigned char flags, const dtPolyRef ref,
float* straightPath, unsigned char* straightPathFlags, dtPolyRef* straightPathRefs,
int* straightPathCount, const int maxStraightPath) const
{
if ((*straightPathCount) > 0 && dtVequal(&straightPath[((*straightPathCount)-1)*3], pos))
{
// The vertices are equal, update flags and poly.
if (straightPathFlags)
straightPathFlags[(*straightPathCount)-1] = flags;
if (straightPathRefs)
straightPathRefs[(*straightPathCount)-1] = ref;
}
else
{
// Append new vertex.
dtVcopy(&straightPath[(*straightPathCount)*3], pos);
if (straightPathFlags)
straightPathFlags[(*straightPathCount)] = flags;
if (straightPathRefs)
straightPathRefs[(*straightPathCount)] = ref;
(*straightPathCount)++;
// If there is no space to append more vertices, return.
if ((*straightPathCount) >= maxStraightPath)
{
return DT_SUCCESS | DT_BUFFER_TOO_SMALL;
}
// If reached end of path, return.
if (flags == DT_STRAIGHTPATH_END)
{
return DT_SUCCESS;
}
}
return DT_IN_PROGRESS;
}
...
- 检查目标点和直线路径列表的最后一个点是否相同（距离足够接近），相同则更新标记信息和多边形，不同则将目标点加入到直线路径列表中，并设置标记信息和多边形。
dtTriArea2D
dtTriArea2D方法的实现如下：
// Detour/Include/DetourCommon.h
...
inline float dtTriArea2D(const float* a, const float* b, const float* c)
{
const float abx = b[0] - a[0];
const float abz = b[2] - a[2];
const float acx = c[0] - a[0];
const float acz = c[2] - a[2];
return acx*abz - abx*acz;
}
...
- 计算向量 AC 和 AB 的叉积，根据右手定则，确定 C 点在 AB 的左侧还是右侧。
- 如果叉积大于 0 ，则 AC 到 AB 为顺时针方向，C 点在 AB 的左侧。
- 如果叉积小于 0 ，则 AC 到 AB 为逆时针方向，C 点在 AB 的右侧。
总结
- 导航网格的寻路算法，还有很多额外的算法，用于处理多种地图情况和多种寻路需求，如：3d网格、非连接网格、移动转向等，这里只介绍基础的算法内容。其中，一些寻路计算的细节，是和导航网格的生成紧密结合的，需要了解导航网格的生成规则，才能更好地理解寻路算法。