字符串匹配,通常会使用暴力匹配算法来进行。而KMP算法是一种改进的字符串匹配算法,在字符串的匹配上通常有较好的表现。
简介
- 字符串匹配应用场景很多,开发过程中经常会使用。将待检查的目标字符串称为主字符串,将用来匹配的字符串称为子字符串,匹配通常采用暴力算法进行,即从主字符串的第一个字符开始,和子字符串逐一字符遍历进行比对。当字符不相同时,则从主字符串的开始,重新和子字符串的逐一字符进行比对。
- 一般情况下,这种匹配方法能有较好的表现。但是,当匹配到某个字符不一样时,往往不需要从主字符串的第二个字符开始重新匹配,因此会出现一些无效的匹配。而 KMP 算法,则对这些无效匹配进行了优化,提高了匹配效率。
- KMP 算法,在某些特殊子字符串下,也出现了一些无效的匹配,所以后续对此算法,又有进一步的改进。
Brute Force
简介
- 暴力算法,就是从头开始,逐一对主字符串进行匹配,当匹配不成功的时候再从下一个字符串开始匹配。

- 从首个字符开始匹配主字符串和子字符串。
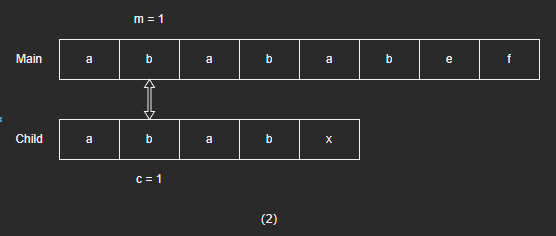
- 字符相同,则都移动到下一个字符继续匹配。
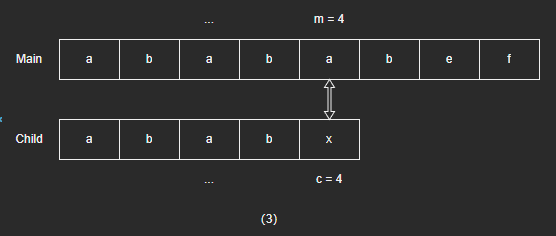
- 一直往后遍历匹配,直到出现字符不相同,则需要回退。

- 第一个字符为首的匹配失败,以第二个字符为首重新开始匹配。
代码示例
public class BruteForce
{
public static int Find(string Main, string Child)
{
// 主字符串 Main 索引
int m = 0;
// 子字符串 Child 索引
int c = 0;
// 当主字符串的索引小于主字符串的长度,且子字符串的索引小于子字符串的长度时,循环进行匹配检查
while (m < Main.Length && c < Child.Length)
{
if (Main[m].Equals(Child[c]))
{
// 如果 Main[m] 和 Child[c] 相同,则移动到下一个位置
m++;
c++;
}
else
{
// 如果 Main[m] 和 Child[c] 不相同,则主字符串的索引回退到首个匹配成功字符的下一个位置,子字符串则重置
m = m - c + 1;
c = 0;
}
}
if (c >= Child.Length)
{
// 如果子字符串索引不小于子字符串的长度,则子字符串匹配完毕,找到了子字符串,匹配成功
return m - c;
}
else
{
// 如果主字符串索引不小于主字符串的长度,则主字符串匹配完毕,没有找到子字符串,匹配失败
return -1;
}
}
}
算法分析
- 假设主字符串的长度为 m ,子字符串的长度为 n,最坏情况下,主字符串的每个字符都要和子字符串的每个字符匹配一次,则时间复杂度为 O(m*n) 。
- 从图(4)可以看出,主字符串和子字符串的第一、二个字符一样,从第三个字符开始不一样,所以主字符串从第二个开始,子字符串从第一个开始,重新进行匹配。但我们知道第二个字符和第一个字符不一样,这一次匹配是肯定失败的,所以这一次匹配其实是可以省略的。KMP 算法,则是对这类遍历进行了优化,省略了很多无效匹配,从而提升了匹配效率。
KMP
简介
- KMP 算法通过分析子字符串的结构,在匹配过程中,省去一部分匹配操作,从而提升效率。
- 回头看前面的示例
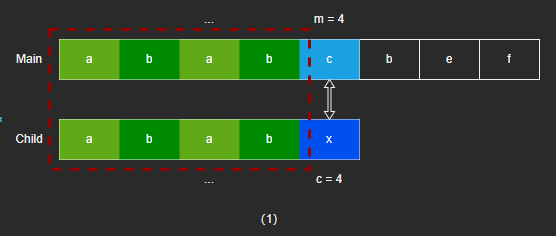
- 当 m = 4 、c = 4 时,Main[4] 和 Child[4] 不相同,主字符串的前4位已经匹配过,和子字符串前4位相同。
- 假设整个字符串的所有字符都互异,则可以将子字符串的首位移动到主字符串的第5位,即 m = 4 、c = 0,因为前4位字符相互肯定不会相同,可以直接跳过。
- 然而,如果存在会相同字符,则需要知道子字符串的前几位和主字符串的后几位字符串是否匹配。
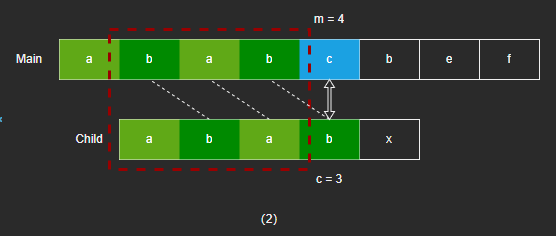
- 如果不相同,则子字符串继续向右移动。
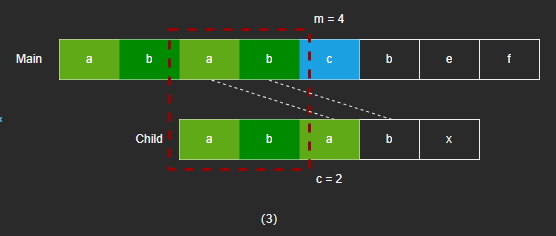
- 如果找到相同的,则可以跳过相同部分,从下一个字符开始匹配。
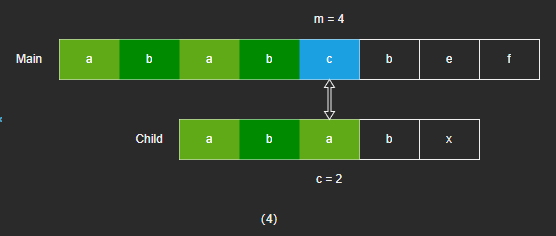
- 可以看到,图(2)(3)中的红框部分比较,其实等价于,主字符串和子字符串相同部分,后缀和前缀的对比。因此只要我们知道,当子字符的某个索引位置匹配失败时,前面部分的后缀和前缀相同的长度是多少,则子字符可以跳过那部分索引,减少了重复匹配的情况,从而提升匹配效率。
- KMP 算法的第一步,就是定义数组 next[] ,长度为子字符串的长度,用来记录每个位置匹配失败时该从哪个位置继续匹配。然后对子字符串进行分析,每个索引前的字符串,前缀和后缀的匹配情况。然后再将主字符串和子字符串进行匹配。
代码示例
- 子字符串处理,获取每个索引对应的下个索引 next[]
public class KMPBase
{
/// <summary>
/// 获取字符串的每个索引对应的下个匹配位置
/// </summary>
/// <param name="child"></param>
/// <returns></returns>
public static int[] GetNext(string child)
{
// 字符串前缀索引(为了简化代码,初始化为 -1,不需要单独判断 prefix 为 0 的情况)
int prefix = -1;
// 字符串后缀索引
int postifx = 0;
// 字符串每个索引不匹配时跳转的索引,即下一个匹配的索引
int[] next = new int[child.Length];
// 初始化索引 0 的 next 值
next[0] = -1;
while (postifx < child.Length - 1)
{
if (prefix < 0 || child[prefix].Equals(child[postifx]))
{
++prefix;
++postifx;
next[postifx] = prefix;
}
else
{
prefix = next[prefix];
}
}
return next;
}
}
- 字符串匹配
public class KMPBase
{
public static int Find(string main, string child)
{
// 初始化子字符串的每个索引对应的下个匹配位置
var next = GetNext(child);
// 主字符串 Main 索引
int m = 0;
// 子字符串 Child 索引
int c = 0;
// 当主字符串的索引小于主字符串的长度,且子字符串的索引小于子字符串的长度时,循环进行匹配检查
while (m < main.Length && c < child.Length)
{
if (main[m].Equals(child[c]))
{
++m;
++c;
}
else
{
// 如果 Main[m] 和 Child[c] 不相同,则子字符串的索引回退到下一个需要检查的位置
c = next[c];
}
}
if (c >= child.Length)
{
// 如果子字符串索引不小于子字符串的长度,则子字符串匹配完毕,找到了子字符串,匹配成功
return m - c;
}
else
{
// 如果主字符串索引不小于主字符串的长度,则主字符串匹配完毕,没有找到子字符串,匹配失败
return -1;
}
}
/// <summary>
/// 获取字符串的每个索引对应的下个匹配位置
/// </summary>
/// <param name="child"></param>
/// <returns></returns>
public static int[] GetNext(string child)
{
// 字符串前缀索引(为了简化代码,初始化为 -1,不需要单独判断 prefix 为 0 的情况)
int prefix = -1;
// 字符串后缀索引
int postifx = 0;
// 字符串每个索引不匹配时跳转的索引,即下一个匹配的索引
int[] next = new int[child.Length];
// 初始化索引 0 的 next 值
next[0] = -1;
while (postifx < child.Length - 1)
{
if (prefix < 0 || child[prefix].Equals(child[postifx]))
{
++prefix;
++postifx;
next[postifx] = prefix;
}
else
{
prefix = next[prefix];
}
}
return next;
}
}
算法分析
- 假设主字符串的长度为 m ,子字符串的长度为 n,分别进行分析。
- 对子字符串求 next 过程,后缀 postfix 一直增加,而前缀 prefix 可能随 postfix 一起增加,也可能减少。减到 -1 时,只能继续随postfix增加。
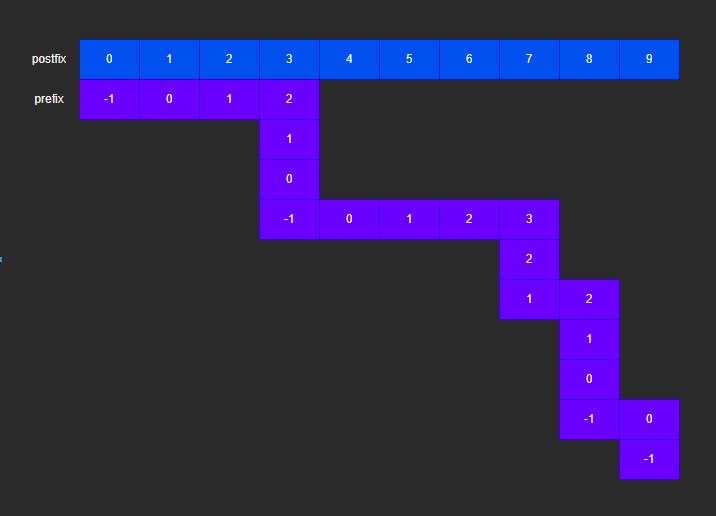
- 可以看到,prefix 的变化,可以分为增加部分和减少部分,增加部分最多只能变化 n - 1 次,即最多只能和 postfix 增加一样的大小,而减少部分也最多只能变化 n - 1 次,即只能减少增加的部分,因此子字符串的时间复杂度为 O(n)。
- 对主字符串的匹配过程也相似,即最多变化 2(m - 1) 次,所以时间复杂度为 O(m)。
- 因此总的复杂度为 O(m+n)。
KMP 改进版
简介
- 再看前面的示例
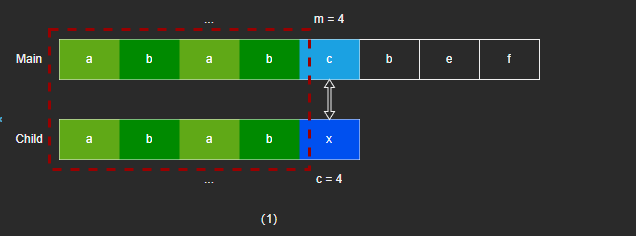
- 当匹配到第五个字符不相同时,根据 KMP 算法,子字符串回退到 c = 2 继续匹配。
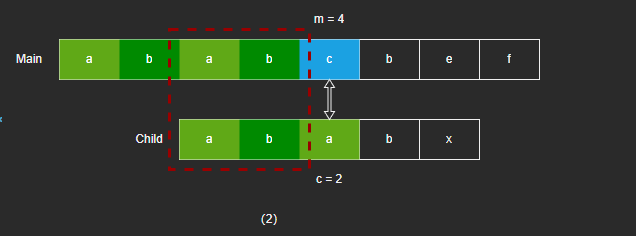
- c = 2 匹配失败,子字符串回退到 c = 0 继续匹配。
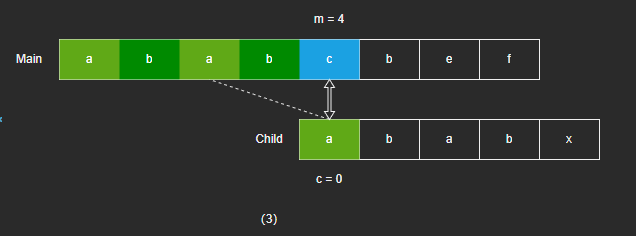
- c = 0 匹配失败,主字符串和子字符串都继续向右移动。
- 可以发现,其实图(2)匹配失败后,图(3)匹配是必定会失败的,因为 Child[0] 和 Child[2] 相同是已知的,所以图(2)的匹配可以省略,直接回退到 c = 0 。也就是说,当 next[c] 的字符和 next[next[c]] 的字符一样时,可以直接回退到 next[next[c]] 上,直到字符不一样时,再继续进行匹配。KMP 算法改进版,就是在 KMP 的基础上,再进行了回退值的优化。
- KMP 改进算法的第一步,不再使用 next[] 数组来记录,改为使用 nextVal[] 数组来记录下一个匹配的索引,递归找到第一个不相同的 next ,从而减少重复匹配的问题。
代码示例
public class KMPImprove
{
public static int Find(string main, string child)
{
// 初始化子字符串的每个索引对应的下个匹配位置
var nextVal = GetNextVal(child);
// 主字符串 Main 索引
int m = 0;
// 子字符串 Child 索引
int c = 0;
// 当主字符串的索引小于主字符串的长度,且子字符串的索引小于子字符串的长度时,循环进行匹配检查
while (m < main.Length && c < child.Length)
{
if (main[m].Equals(child[c]))
{
++m;
++c;
}
else
{
// 如果 Main[m] 和 Child[c] 不相同,则子字符串的索引回退到下一个需要检查的位置
c = nextVal[c];
}
}
if (c >= child.Length)
{
// 如果子字符串索引不小于子字符串的长度,则子字符串匹配完毕,找到了子字符串,匹配成功
return m - c;
}
else
{
// 如果主字符串索引不小于主字符串的长度,则主字符串匹配完毕,没有找到子字符串,匹配失败
return -1;
}
}
/// <summary>
/// 获取字符串的每个索引对应的下个匹配位置
/// </summary>
/// <param name="child"></param>
/// <returns></returns>
public static int[] GetNextVal(string child)
{
// 字符串前缀索引(为了简化代码,初始化为 -1,不需要单独判断 prefix 为 0 的情况)
int prefix = -1;
// 字符串后缀索引
int postifx = 0;
// 字符串每个索引不匹配时跳转的索引,即下一个匹配的索引
int[] nextVal = new int[child.Length];
// 初始化索引 0 的 nextVal 值
nextVal[0] = -1;
while (postifx < child.Length - 1)
{
if (prefix < 0 || child[prefix].Equals(child[postifx]))
{
++prefix;
++postifx;
// // 前缀和后缀字符相同,且下一个字符如果和其回退索引 next[index] 的字符相同,则需要回退到再上一个回退索引,即 next[next[index]]
if (child[postifx].Equals(child[prefix]))
{
nextVal[postifx] = nextVal[prefix];
}
else
{
// // 前缀和后缀字符相同,且下一个字符如果和其回退索引 next[index] 的字符不相同,则回退到相同前缀的下一个字符
nextVal[postifx] = prefix;
}
}
else
{
// 如果前缀和后缀不相同,则缩短前缀,回退到上一个索引
prefix = nextVal[prefix];
}
}
return nextVal;
}
}
算法分析
- 假设主字符串的长度为 m ,子字符串的长度为 n,改进版的 KMP 算法只是增加了一些剪枝的情况, 因此总的复杂度还是为 O(m+n)。
总结
- KMP 算法,大多数情况下,对字符串的遍历有较大的性能提升,而改进的版本,进一步减少了无效的遍历,从而能有更好的表现。算法本身并不算非常复杂,可以看到代码量相对也比较少,只要理清楚整体的流程,以及了解如何推导其时间复杂度,基本上就能很好地掌握这个算法。