A* 寻路算法是常用的寻路方法,JPS寻路在A* 的基础上,进行跳点剪枝优化,提升了寻路性能。
简介
- A* 算法,会维护一个最小堆。由于频繁加入、删除点,就需要经常更新最小堆。而JPS算法,则减少了需要更新的节点数量,从而提升了寻路的效率。
跳点剪枝
相关定义
- x :当前节点。
- p(x) :x 的父节点 。
- neighbours(x) :x 的所有邻居节点。
- d :p(x) 到 x 的方向。
邻居修剪规则(Neighbour Pruning Rules)
- 修剪规则包含以下情况:
- x 为起点,即 p(x) 为 null。
- 不需要修剪。
- p(x) 到 x 为直线移动(即水平方向或竖直方向)。
- 对于 neighbours(x) 中的任意一个邻居节点 n ,如果从 p(x) 到 n (不经过 x)的路径不大于从 p(x) 到 n (经过 x)的路径,则 n 需要修剪。


- 对于 neighbours(x) 中的任意一个邻居节点 n ,如果从 p(x) 到 n (不经过 x)的路径不大于从 p(x) 到 n (经过 x)的路径,则 n 需要修剪。
- p(x) 到 x 为对角线移动。
- 对于 neighbours(x) 中的任意一个邻居节点 n ,如果从 p(x) 到 n (不经过 x)的路径小于从 p(x) 到 n (经过 x)的路径,则 n 需要修剪。


- 对于 neighbours(x) 中的任意一个邻居节点 n ,如果从 p(x) 到 n (不经过 x)的路径小于从 p(x) 到 n (经过 x)的路径,则 n 需要修剪。
- x 为起点,即 p(x) 为 null。
- 如图中所示,红色节点为障碍点,灰色节点为需要修剪的,而绿色节点则是符合条件,不需要修剪的。
- 也就是说,根据最优路径选择,当前 x 认为是最优路径上的节点,因此到下一个节点,经过 x 的路径应该是最优的,不应该存在有其他路径更优(即比此路径更短)。
自然邻居(Natural Neighbour)
- 假设 neighbours(x) 中没有障碍点时,经过邻居修剪规则后,剩下的点(浅绿色)称为自然邻居。


- 如图,对于直线移动,x 的邻居中有障碍点(节点 2),则假设 x 的邻居中没有障碍点,修剪完后剩下的节点 6 ,即为自然邻居。


- 同样,对于对角线移动,节点 2、3、6 为自然邻居。
强制邻居(Forced Neighbour)
- n 为 neighbours(x) 中的一个节点,如果 n 为强制邻居,则需要满足:
- n 不是 x 的自然邻居。
- 从 p(x) 到 n (经过 x)的路径小于从 p(x) 到 n (不经过 x)的路径。
- 可以看到,修剪过后,剩下的节点为 3、6,其中节点 6 为自然邻居,则节点 3 为强制邻居。

- 同样,对角线移动时,修剪过后剩下节点 1、2、3、6,其中节点 2、3、6 为自然邻居,则节点 3 为强制邻居。

跳点(Jump Point)
- 当前方向为 d ,当前节点为 x ,如果节点 y 为节点 x 的跳点,则存在一个最小值 k ,使得节点 y 满足 y = x + kd ,并且满足以下其中一个条件:
- 条件1 :节点 y 为目标节点。
- 条件2 :节点 y 至少有一个强制邻居。
- 条件3 :方向 d 为对角线移动,且存在节点 z ,满足 z = y + k_i * d_i ,并且满足条件1或条件2,使得节点 z 为节点 y 的跳点。其中
- k_i : 自然数 N。
- d_i : 与当前方向夹角为45度的方向,即水平和竖直方向。
- 上面规则也可以描述为:
- 当前方向 d 为直线移动,如果此方向上存在一个节点 y 为目标节点,或者节点 y 有一个强制邻居,则节点 y 为节点 x 的跳点。
- 当前方向 d 为对角线移动,如果此方向上存在一个节点 y ,沿着此方向的水平或竖直方向的直线移动能找到节点 y 的跳点,则节点 y 为节点 x 的跳点。
- 如图,节点 z(蓝色)为目标节点,当直线移动时,找到节点 y 为强制邻居,所以节点 y 为跳点。
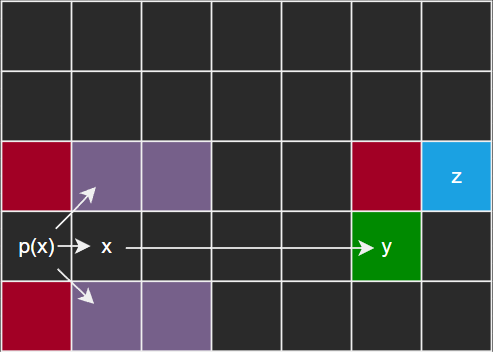
- 当对角线移动时,沿当前方向以及水平竖直方向寻找,找到节点 y ,沿节点 y 的水平方向找到目标节点 z ,即找到跳点,因此节点 y 为跳点。
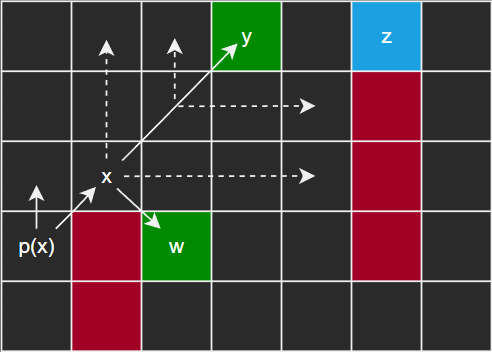
拐点(Turning Point)
- 路径上的一个节点 n_k-1 到节点 n_k 的方向和节点 n_k 到节点 n_k+1 的方向不同时,则节点 n_k 为拐点。
- 拐点有三种情况:
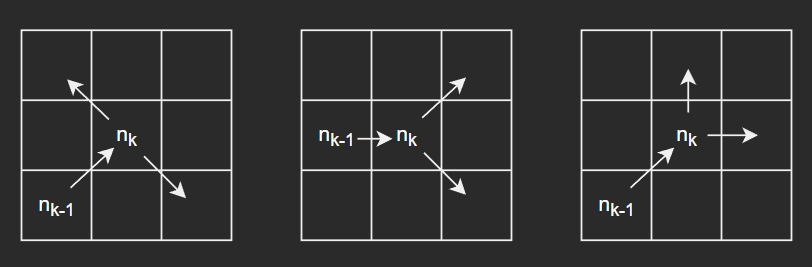
- 从对角到另一个对角移动。
- 从直线到对角移动。
- 从对角到直线移动。
对角线优先(diagonal-first)
- 如果路径上不存在从直线到对角的拐点,替换为从对角到直线的拐点后,仍保持路径长度不变,则此路径为对角线优先。
- 一般情况下,从直线到对角的拐点应该都可等价替换为从对角到直线的拐点。当无法替换时,即存在障碍,使得无法先进行对角移动。
- 最优的对角线优先路径上的每一个拐点,都是一个跳点。对三种拐点进行分析:
- 拐点为从对角到另一个对角。
- 由于当前路径为最优路径,所以必然存在有障碍点,使得 n_k-1 无法直线移动到 n_k+1 ,必须对角移动到 n_k 再对角移动到 n_k+1 ,此时 n_k 为拐点。
- 由于 neighbours(n_k) 存在障碍点,并且 n_k-1 到 n_k+1 (经过 n_k)为最小路径, 所以 n_k+1 为 n_k 的强制邻居。
- 由于 n_k = n_k-1 + d ,且 n_k 有强制邻居,所以 n_k 为跳点。
- 拐点为从直线到对角。
- 由于当前为对角线优先路径,所以 neighbours(n_k) 存在障碍,使得 n_k-1 无法先进行对角移动,所以 n_k-1 到 n_k+1 (经过 n_k)的路径为最小路径,即 n_k+1 为 n_k 的强制邻居,则拐点 n_k 也为跳点。
- 拐点为从对角到直线。
- 这种情况下,有两种可能。一是沿着直线方向能到达目标节点,二是沿着直线方向有另一个拐点。
- 如果沿着直线方向能到达目标节点,即 n_k 到 n_k+1 的方向上存在目标节点,则目标节点为当前拐点的跳点,即满足跳点的条件3,所以当前拐点 n_k 也为跳点。
- 如果沿着直线方向有另一个拐点,根据从直线到对角的情况,下一个拐点为跳点,所以下一个拐点为当前拐点的跳点,满足跳点的条件3,所以当前拐点 n_k 也为跳点。
- 拐点为从对角到另一个对角。
相关定理
- 使用跳点剪枝进行搜索总会得到最优解。证明流程如下:
- 假设路径 π 为两个节点之间任意选择的最优路径,将路径 π 转化为对角线优先路径 π' 。
- 将路径 π' 拆分成一系列相邻的段,即 π' = π_0' + π_1' + … + π_n' 。
- 每段路径 π_i' 都只有一个方向,即 n_0_ 沿着一个方向前进到 n_k 。
- 对于每一段路径 π_i' ,从起点 n_0 到终点 n_k ,使用跳点算法计算时,都不需要对中间的任意节点进行展开搜索,因为从 n_0 到 n_k 的路径一定是最优的。
- 由于对角线优先路径的拐点也为跳点,所以每个拐点都需要展开搜索。
- 开始节点必须在每次搜索开始时展开,而目标节点定义为一个跳跃点,因此两者都得到了扩展。
伪代码算法
算法1 确定后继节点(Identify Successors)
- 相关定义:
- x :当前节点。
- s :起始节点。
- g :目标节点。
- successors(x) :x 节点的所有后继节点集合。
- 算法流程:
- 通过邻居修剪规则,修剪 x 的邻居。
- 遍历修剪后的邻居节点,使用跳点方法(Function jump),判断邻居节点是否为跳点。
- 如果邻居节点为跳点,则加入 successors(x) 中。
- 返回 successors(x) 集合。
算法2 跳点方法(Function jump)
- 相关定义:
- x :初始节点。
- d :前进方向。
- s :起始节点。
- g :目标节点。
- 算法流程:
- 节点 n 为 x 沿着当前方向 d 移动一步。
- 如果 n 为阻挡或者超出节点边界,则返回 null。
- 如果 n 为 g ,则返回 n 。
- 如果 n 有强制邻居,则返回 n 。
- 如果 d 为对角方向,则对水平方向 d_1 和竖直方向 d_2 ,调用跳点方法 jump(n, d_i, s, g) ,检查是否为跳点,如果是则返回 n 。
- 沿当前方向,递归调用跳点方法 jump(n, d, s, g) 并返回。
算法3 计算对角线优先路径(Compute Diagonal First Path)
- 相关定义:
- π :任意最优长度路径。
- 算法流程:
- 选择在 π 上出现的一对相邻边,其中 (n_k−1, n_k_) 是直线移动,(n_k, n_k+1) 是对角线移动。
- 将当前的相邻边替换为另一对可移动的相邻边,其中 (n_k−1, n_k') 是对角线移动,(n_k', n_k+1) 是直线移动,即 n_k' 不为障碍点。
- 重复上面步骤,直到没有可以替换的相邻边。
- 返回 π ,得到对角线优先路径。