距离变换是计算并标识空间点(对目标点)距离的过程,其中 EDT(Euclidean Distance Transform),欧式距离变换精度高,与实际距离相符,应用更广泛。
简介
- 在二值图像中,白色代表目标点,黑色代表背景点,EDT 能将二值图转化为灰度图,其中每个栅格的灰度值等于它到最近的背景点的距离。
- EDT 有多类算法,主要有:
- 暴力算法
- 光栅扫描算法
- 独立扫描算法
- 传播算法
- 算法不同,实现效率也不一样,后面会介绍各类算法的实现细节,这里先定义一些通用概念:
- width : 图像宽度
- height : 图像高度
- colorMap : 整个图像的颜色值
暴力算法(Brute Force)
简介
- 暴力算法,顾名思义,就是计算二值图像中每一个白色点到每一个黑色点的距离,取其中的最小值,则为该点的距离。
伪代码
- 遍历图像的每一个点,对于点 (i, j)
- 如果点 (i, j) 为黑色,则该点距离为 0
- 如果点 (i, j) 为白色,则遍历图像的每一个点,对于点 (m, n)
- 如果点 (m, n) 为黑色,计算点 (i, j) 到点 (m, n) 的距离
- 比较计算得到的距离,取最小值,则为点 (i, j) 的距离
算法分析
- 对于每一个点,都需要遍历一遍所有点,来计算距离。假设图片的宽高都为 n ,则时间复杂度为 O(n^4) 。
- 暴力算法是最基础的算法,尽管时间复杂度高,但是算法相对简单,对一些离线生成的情况来说,还是在可接受的范围内。
光栅扫描算法(Raster Scanning)
简介
- EDT 算法中,使用最广泛的算法之一,是 Danielsson 在 1980 年提出的 4SED(4-point Sequential Euclidean Distance Transform)算法。尽管该算法相对简单且有效,但不是准确的。经过后续的各种优化,8SSEDT(8-point Signed Sequential Euclidean Distance Transform)是比较常用的光栅扫描算法。
- 8SSEDT 算法,对于图像的每一个点,需要记录其到黑色点的相对坐标信息,即
- dx :水平相对坐标。
- dy :竖直相对坐标。
- 距离
- 通过坐标来计算,即 dx * dx + dy * dy 。
- 基于邻居点的距离
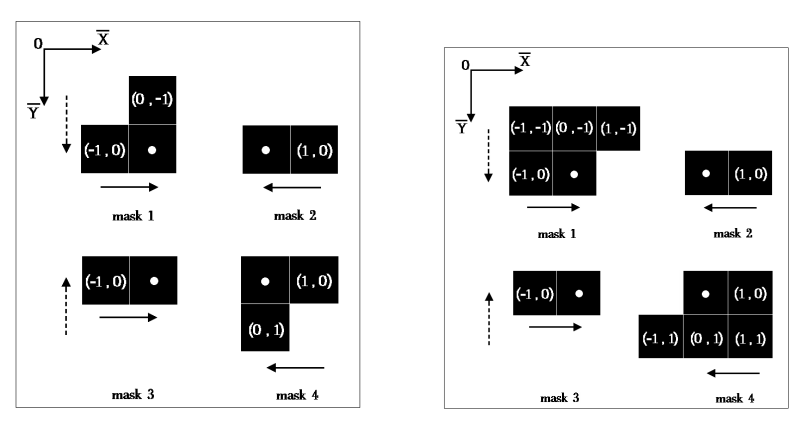
- 邻居点的坐标,加上邻居点相对于点 (i, j) 的权重(即偏移坐标),得到的新坐标的距离,则为基于邻居点的距离。当 (0, 0) 点在左上角时,偏移坐标为:
- 左:(-1, 0)
- 上:(0, -1)
- 右:(1, 0)
- 下:(0, 1)
- 左上:(-1, -1)
- 右上:(1, -1)
- 左下:(-1, 1)
- 右下:(1, 1)
- 邻居点的坐标,加上邻居点相对于点 (i, j) 的权重(即偏移坐标),得到的新坐标的距离,则为基于邻居点的距离。当 (0, 0) 点在左上角时,偏移坐标为:
伪代码
- 初始化
- 遍历图像的每一个点,进行初始化,对于点 (i, j)
- 如果点 (i, j) 为白色,则设置 dx、dy 为无穷大(通常设置为图像的宽高)
- 如果点 (i, j) 为黑色,则设置 dx、dy 为 0
- 遍历图像的每一个点,进行初始化,对于点 (i, j)
- 从上到下扫描
- 对当前行,从左到右扫描,对每个点进行处理
- 计算点 (i, j) 的距离
- 分别计算点 (i, j) 基于邻居点左、上、左上、右上的距离,取其中的最小距离,如果点 (i, j) 的距离大于最小距离,则将点 (i, j) 的坐标更新为最小距离的邻居点的坐标加上权重得到的新坐标。
- 对当前行,从右到左扫描,对每个点进行处理
- 计算点 (i, j) 的距离
- 分别计算点 (i, j) 基于邻居点右的距离,如果点 (i, j) 的距离大于基于邻居点右的距离,则将点 (i, j) 的坐标更新为邻居点右的坐标加上权重得到的新坐标。
- 对当前行,从左到右扫描,对每个点进行处理
- 从下到上扫描
- 对当前行,从右到左扫描,对每个点进行处理
- 计算点 (i, j) 的距离
- 分别计算点 (i, j) 基于邻居点右、下、左下、右下的距离,取其中的最小距离,如果点 (i, j) 的距离大于最小距离,则将点 (i, j) 的坐标更新为最小距离的邻居点的坐标加上权重得到的新坐标。
- 对当前行,从左到右扫描,对每个点进行处理
- 计算点 (i, j) 的距离
- 分别计算点 (i, j) 基于邻居点左的距离,如果点 (i, j) 的距离大于基于邻居点右的距离,则将点 (i, j) 的坐标更新为邻居点右的坐标加上权重得到的新坐标。
- 对当前行,从右到左扫描,对每个点进行处理
算法分析
- 8SSEDT 算法,进行了4次扫描,每次扫描都会比较部分邻居点,即每次扫描都是在线性时间内完成。假设图片的宽高都为 n ,则时间复杂度为 O(n^2) 。
- 相比暴力算法,性能上有了较大的提升。通过使用坐标表示,计算基于邻居点的距离时,可以减少大量平方根的运算。
独立扫描算法(Independent Scanning)
简介
- Saito 和 Toriwaki [Saito and Toriwaki 1994] 设计了一种算法对 k 维图像进行 k 变换来产生EDT,每个坐标方向一个变换。对于 2D 图像,首先沿着每一行计算距离值(第一个变换),然后使用这些值计算每列的最小距离(第二次变换)。
-
变换一:给定输入图像 F,独立扫描的第一个变换产生图像 G ,则 G(i, j) 为点 (i, j) 到同一行中最近的黑色点的距离,这种变换是通过执行向前扫描(即从左到右),然后在图像的每一行进行向后扫描来有效地实现的。
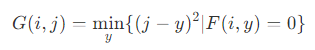
-
变换二:从变换一的 G 开始,变换产生一个图像 S ,它是 F 的距离映射。对于点 (i,j) 所在的列,点 (i, j) 到当前列的每一个点 (x, j) 的距离(即到每一行的距离),加上 G(x, j) 的值,其中的最小值,则为点 (i, j) 在 F 中的距离,即 S(i, j)。
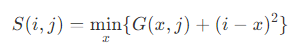
-
伪代码

- 变换一,对图像的每一行,进行两次扫描
- 从左到右扫描,对于点 (i, j)
- 如果点 (i, j) 为黑色点,则设置 G(i, j) 为 0 ,记录或更新黑色点的位置。
- 如果点 (i, j) 为白色点,则设置 G(i, j) 为当前点到左侧黑色点的距离,如果没有黑色点则设置为图像的宽度值。
- 从右到左扫描,对于点 (i, j)
- 如果点 (i, j) 为黑色点,则设置 G(i, j) 为 0 ,记录或更新黑色点的位置。
- 如果点 (i, j) 为白色点,计算当前点到右侧黑色点的距离,如果没有黑色点则设置为图像的宽度值。如果计算得到的距离小于 G(i, j) 的值,则更新 G(i, j) 的值为新的距离。
- 从左到右扫描,对于点 (i, j)
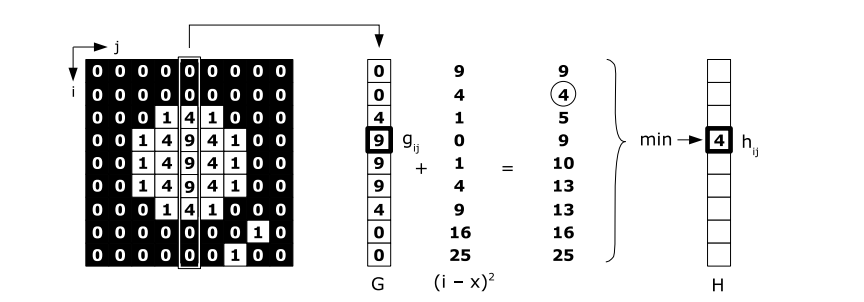
- 变换二,遍历图像的每个点,对于点 (i, j)
- 计算点 (i, j) 到当前列的每一个点 (x, j) 的距离,其中 x 为 [0, height - 1]。
- 将点 (i, j) 到当前列点 (x, j) 的距离,分别加上 G(x, j) 的值,取其中的最小值,则为点 (i, j) 的距离。
算法分析
- 假设图片的宽高都为 n ,对于变换一,对于每一行,通过采用两遍扫描的方式,实现在线性时间下,计算每个点的水平距离。而对于变换二,每个点需要计算和当前列每个点的距离,则最终算法的时间复杂度为 O(n^3) 。
- 相比 8SSEDT 算法,Saito 的算法尽管效率没有那么高,但它很容易编码,并且它很方便扩展到 3D 情况中。
算法对比

- 以上图为样本,对各种尺寸的样本进行算法计算,其中
- 正:原样本图
- 反:样本图黑白反色
- 各种算法耗时情况如下表:
| 图片尺寸 | 暴力算法(ms) | 光栅扫描算法(ms) | 独立扫描算法(ms) |
|---|---|---|---|
| 64 x 64(正) | 28.37 | 4.99 | 2.99 |
| 64 x 64(反) | 136.45 | 3.99 | 2.98 |
| 128 x 128(正) | 359.42 | 16.95 | 23.43 |
| 128 x 128(反) | 2175.82 | 16.98 | 24.93 |
| 256 x 256(正) | 5359.35 | 67.14 | 187.76 |
| 256 x 256(反) | 34540.57 | 68.25 | 186.51 |
| 512 x 512(正) | 87196.00 | 273.38 | 1474.67 |
| 512 x 512(反) | 569392.50 | 274.32 | 1478.42 |
| 1024 x 1024(正) | - | 1112.65 | 11766.52 |
| 1024 x 1024(反) | - | 1109.51 | 11755.97 |
| 2048 x 2048(正) | - | 5420.58 | 93695.14 |
| 2048 x 2048(反) | - | 5401.31 | 93836.86 |
总结
- 暴力算法在一定范围内,由于实现简单,一定程度上耗时还是相对能接受的。
- 独立扫描算法表现较好,但处理较大图片的时候耗时相对还是较高,但是算法相对简单,方便扩展。
- 光栅扫描算法是其中表现最好的,对于 2048 x 2048 的图片,耗时也相对较低,因此也是使用相对较广泛的算法。
示例工程
参考
- A Note on “Fast Raster Scan Distance Propagation on the Discrete Rectangular Lattice”
- 2D Euclidean Distance Transform Algorithms: A Comparative Survey